TFT

In summary Temporal Fusion Transformer (TFT) combines gating layers, an LSTM recurrent encoder, with multi-head attention layers for a multi-step forecasting strategy decoder. TFT’s inputs are static exogenous

\mathbf{x}^{(s)}

, historic exogenous

\mathbf{x}^{(h)}_{[:t]}

, exogenous available at the time of the prediction

\mathbf{x}^{(f)}_{[:t+H]}

and autorregresive features

\mathbf{y}_{[:t]}

, each of these inputs is further decomposed into categorical and continuous. The network uses a multi-quantile regression to model the following conditional probability:

\mathbb{P}(\mathbf{y}_{[t+1:t+H]}|\;\mathbf{y}_{[:t]},\; \mathbf{x}^{(h)}_{[:t]},\; \mathbf{x}^{(f)}_{[:t+H]},\; \mathbf{x}^{(s)})

References

Jan Golda, Krzysztof Kudrynski. “NVIDIA, Deep Learning Forecasting Examples”
Bryan Lim, Sercan O. Arik, Nicolas Loeff, Tomas Pfister, “Temporal Fusion Transformers for interpretable multi-horizon time series forecasting”

Figure 1. Temporal Fusion Transformer Architecture.

1. Temporal Fusion Decoder

`TFT`

TFT(
    h,
    input_size,
    tgt_size=1,
    stat_exog_list=None,
    hist_exog_list=None,
    futr_exog_list=None,
    hidden_size=128,
    n_head=4,
    attn_dropout=0.0,
    grn_activation="ELU",
    n_rnn_layers=1,
    rnn_type="lstm",
    one_rnn_initial_state=False,
    dropout=0.1,
    loss=MAE(),
    valid_loss=None,
    max_steps=1000,
    learning_rate=0.001,
    num_lr_decays=-1,
    early_stop_patience_steps=-1,
    val_monitor="ptl/val_loss",
    val_check_steps=100,
    batch_size=32,
    valid_batch_size=None,
    windows_batch_size=1024,
    inference_windows_batch_size=1024,
    start_padding_enabled=False,
    training_data_availability_threshold=0.0,
    step_size=1,
    scaler_type="robust",
    random_seed=1,
    drop_last_loader=False,
    alias=None,
    optimizer=None,
    optimizer_kwargs=None,
    lr_scheduler=None,
    lr_scheduler_kwargs=None,
    dataloader_kwargs=None,
    **trainer_kwargs
)

Bases: BaseModel TFT The Temporal Fusion Transformer architecture (TFT) is an Sequence-to-Sequence model that combines static, historic and future available data to predict an univariate target. The method combines gating layers, an LSTM recurrent encoder, with and interpretable multi-head attention layer and a multi-step forecasting strategy decoder. Parameters:

Name	Type	Description	Default
`h`	`int`	Forecast horizon.	required
`input_size`	`int`	autorregresive inputs size, y=[1,2,3,4] input_size=2 -> y_[t-2:t]=[1,2].	required
`tgt_size`	`int`	target size.	`1`
`stat_exog_list`	`str list`	static continuous columns.	`None`
`hist_exog_list`	`str list`	historic continuous columns.	`None`
`futr_exog_list`	`str list`	future continuous columns.	`None`
`hidden_size`	`int`	units of embeddings and encoders.	`128`
`n_head`	`int`	number of attention heads in temporal fusion decoder.	`4`
`attn_dropout`	`float`	dropout of fusion decoder’s attention layer.	`0.0`
`grn_activation`	`str`	activation for the GRN module from [‘ReLU’, ‘Softplus’, ‘Tanh’, ‘SELU’, ‘LeakyReLU’, ‘Sigmoid’, ‘ELU’, ‘GLU’, ‘GELU’].	`’ELU’`
`n_rnn_layers`	`int`	number of RNN layers.	`1`
`rnn_type`	`str`	recurrent neural network (RNN) layer type from [“lstm”,“gru”].	`‘lstm’`
`one_rnn_initial_state`	`str`	Initialize all rnn layers with the same initial states computed from static covariates.	`False`
`dropout`	`float`	dropout of inputs VSNs.	`0.1`
`loss`	`PyTorch module`	instantiated train loss class from losses collection.	`MAE()`
`valid_loss`	`PyTorch module`	instantiated valid loss class from losses collection.	`None`
`max_steps`	`int`	maximum number of training steps.	`1000`
`learning_rate`	`float`	Learning rate between (0, 1).	`0.001`
`num_lr_decays`	`int`	Number of learning rate decays, evenly distributed across max_steps.	`-1`
`early_stop_patience_steps`	`int`	Number of validation iterations before early stopping.	`-1`
`val_monitor`	`str`	metric to monitor for early stopping. Valid options: “ptl/val_loss”, “valid_loss”, “train_loss”. Default: “ptl/val_loss”.	`‘ptl/val_loss’`
`val_check_steps`	`int`	Number of training steps between every validation loss check.	`100`
`batch_size`	`int`	number of different series in each batch.	`32`
`valid_batch_size`	`int`	number of different series in each validation and test batch.	`None`
`windows_batch_size`	`int`	windows sampled from rolled data, default uses all.	`1024`
`inference_windows_batch_size`	`int`	number of windows to sample in each inference batch, -1 uses all.	`1024`
`start_padding_enabled`	`bool`	if True, the model will pad the time series with zeros at the beginning, by input size.	`False`
`training_data_availability_threshold`	`Union[float, List[float]]`	minimum fraction of valid data points required for training windows. Single float applies to both insample and outsample; list of two floats specifies [insample_fraction, outsample_fraction]. Default 0.0 allows windows with only 1 valid data point (current behavior).	`0.0`
`step_size`	`int`	step size between each window of temporal data.	`1`
`scaler_type`	`str`	type of scaler for temporal inputs normalization see temporal scalers.	`‘robust’`
`random_seed`	`int`	random seed initialization for replicability.	`1`
`drop_last_loader`	`bool`	if True `TimeSeriesDataLoader` drops last non-full batch.	`False`
`alias`	`str`	optional, Custom name of the model.	`None`
`optimizer`	`Subclass of ‘torch.optim.Optimizer’`	optional, user specified optimizer instead of the default choice (Adam).	`None`
`optimizer_kwargs`	`dict`	optional, list of parameters used by the user specified `optimizer`.	`None`
`lr_scheduler`	`Subclass of ‘torch.optim.lr_scheduler.LRScheduler’`	optional, user specified lr_scheduler instead of the default choice (StepLR).	`None`
`lr_scheduler_kwargs`	`dict`	optional, list of parameters used by the user specified `lr_scheduler`.	`None`
`dataloader_kwargs`	`dict`	optional, list of parameters passed into the PyTorch Lightning dataloader by the `TimeSeriesDataLoader`.	`None`
`**trainer_kwargs`	`int`	keyword trainer arguments inherited from PyTorch Lighning’s trainer.

`TFT.fit`

fit(
    dataset, val_size=0, test_size=0, random_seed=None, distributed_config=None
)

Fit. The fit method, optimizes the neural network’s weights using the initialization parameters (learning_rate, windows_batch_size, …) and the loss function as defined during the initialization. Within fit we use a PyTorch Lightning Trainer that inherits the initialization’s self.trainer_kwargs, to customize its inputs, see PL’s trainer arguments. The method is designed to be compatible with SKLearn-like classes and in particular to be compatible with the StatsForecast library. By default the model is not saving training checkpoints to protect disk memory, to get them change enable_checkpointing=True in __init__. Parameters:

Name	Type	Description	Default
`dataset`	`TimeSeriesDataset`	NeuralForecast’s `TimeSeriesDataset`, see documentation.	required
`val_size`	`int`	Validation size for temporal cross-validation.	`0`
`random_seed`	`int`	Random seed for pytorch initializer and numpy generators, overwrites model.init’s.	`None`
`test_size`	`int`	Test size for temporal cross-validation.	`0`

Returns:

Type	Description
None

`TFT.predict`

predict(
    dataset,
    test_size=None,
    step_size=1,
    random_seed=None,
    quantiles=None,
    h=None,
    explainer_config=None,
    **data_module_kwargs
)

Predict. Neural network prediction with PL’s Trainer execution of predict_step. Parameters:

Name	Type	Description	Default
`dataset`	`TimeSeriesDataset`	NeuralForecast’s `TimeSeriesDataset`, see documentation.	required
`test_size`	`int`	Test size for temporal cross-validation.	`None`
`step_size`	`int`	Step size between each window.	`1`
`random_seed`	`int`	Random seed for pytorch initializer and numpy generators, overwrites model.init’s.	`None`
`quantiles`	`list`	Target quantiles to predict.	`None`
`h`	`int`	Prediction horizon, if None, uses the model’s fitted horizon. Defaults to None.	`None`
`explainer_config`	`dict`	configuration for explanations.	`None`
`**data_module_kwargs`	`dict`	PL’s TimeSeriesDataModule args, see documentation.

Returns:

Type	Description
None

`TFT.feature_importances`

feature_importances()

Compute the feature importances for historical, future, and static features. Returns:

Name	Type	Description
`dict`		A dictionary containing the feature importances for each feature type. The keys are ‘hist_vsn’, ‘future_vsn’, and ‘static_vsn’, and the values are pandas DataFrames with the corresponding feature importances.

`TFT.attention_weights`

attention_weights()

Batch average attention weights Returns: np.ndarray: A 1D array containing the attention weights for each time step.

`TFT.feature_importance_correlations`

feature_importance_correlations()

Compute the correlation between the past and future feature importances and the mean attention weights. Returns: pd.DataFrame: A DataFrame containing the correlation coefficients between the past feature importances and the mean attention weights.

Usage Example

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from neuralforecast import NeuralForecast

# from neuralforecast.models import TFT
from neuralforecast.losses.pytorch import DistributionLoss
from neuralforecast.utils import AirPassengersPanel, AirPassengersStatic

AirPassengersPanel["month"] = AirPassengersPanel.ds.dt.month
Y_train_df = AirPassengersPanel[
    AirPassengersPanel.ds < AirPassengersPanel["ds"].values[-12]
]  # 132 train
Y_test_df = AirPassengersPanel[
    AirPassengersPanel.ds >= AirPassengersPanel["ds"].values[-12]
].reset_index(drop=True)  # 12 test

nf = NeuralForecast(
    models=[
        TFT(
            h=12,
            input_size=48,
            hidden_size=20,
            grn_activation="ELU",
            rnn_type="lstm",
            n_rnn_layers=1,
            one_rnn_initial_state=False,
            loss=DistributionLoss(distribution="StudentT", level=[80, 90]),
            learning_rate=0.005,
            stat_exog_list=["airline1"],
            futr_exog_list=["y_[lag12]", "month"],
            hist_exog_list=["trend"],
            max_steps=300,
            val_check_steps=10,
            early_stop_patience_steps=10,
            scaler_type="robust",
            windows_batch_size=None,
            enable_progress_bar=True,
        ),
    ],
    freq="ME",
)
nf.fit(df=Y_train_df, static_df=AirPassengersStatic, val_size=12)
Y_hat_df = nf.predict(futr_df=Y_test_df)

# Plot quantile predictions
Y_hat_df = Y_hat_df.reset_index(drop=False).drop(columns=["unique_id", "ds"])
plot_df = pd.concat([Y_test_df, Y_hat_df], axis=1)
plot_df = pd.concat([Y_train_df, plot_df])

plot_df = plot_df[plot_df.unique_id == "Airline1"].drop("unique_id", axis=1)
plt.plot(plot_df["ds"], plot_df["y"], c="black", label="True")
plt.plot(plot_df["ds"], plot_df["TFT"], c="purple", label="mean")
plt.plot(plot_df["ds"], plot_df["TFT-median"], c="blue", label="median")
plt.fill_between(
    x=plot_df["ds"][-12:],
    y1=plot_df["TFT-lo-90"][-12:].values,
    y2=plot_df["TFT-hi-90"][-12:].values,
    alpha=0.4,
    label="level 90",
)
plt.legend()
plt.grid()
plt.plot()

2. TFT Architecture

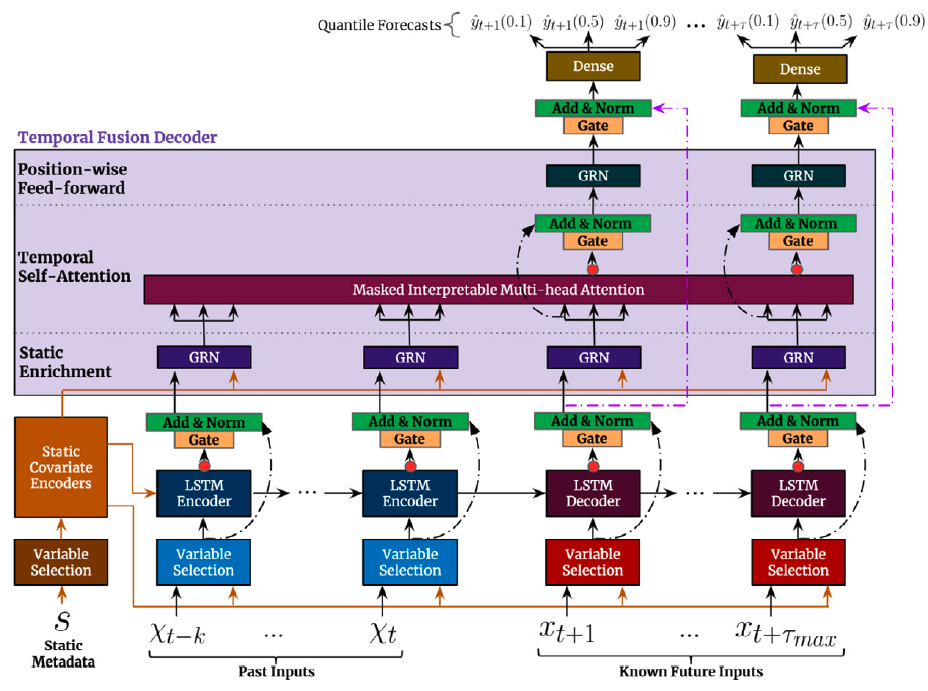
The first TFT’s step is embed the original input

\{\mathbf{x}^{(s)}, \mathbf{x}^{(h)}, \mathbf{x}^{(f)}\}

into a high dimensional space

\{\mathbf{E}^{(s)}, \mathbf{E}^{(h)}, \mathbf{E}^{(f)}\}

, after which each embedding is gated by a variable selection network (VSN). The static embedding

\mathbf{E}^{(s)}

is used as context for variable selection and as initial condition to the LSTM. Finally the encoded variables are fed into the multi-head attention decoder.

2.1 Static Covariate Encoder

The static embedding

\mathbf{E}^{(s)}

is transformed by the StaticCovariateEncoder into contexts

c_{s}, c_{e}, c_{h}, c_{c}

. Where

c_{s}

are temporal variable selection contexts,

c_{e}

are TemporalFusionDecoder enriching contexts, and

c_{h}, c_{c}

are LSTM’s hidden/contexts for the TemporalCovariateEncoder.

2.2 Temporal Covariate Encoder

TemporalCovariateEncoder encodes the embeddings

\mathbf{E}^{(h)}, \mathbf{E}^{(f)}

and contexts

(c_{h}, c_{c})

with an LSTM. An analogous process is repeated for the future data, with the main difference that

\mathbf{E}^{(f)}

contains the future available information.

2.3 Temporal Fusion Decoder

The TemporalFusionDecoder enriches the LSTM’s outputs with

c_{e}

and then uses an attention layer, and multi-step adapter.

3. Interpretability

3.1 Attention Weights

attention = nf.models[0].attention_weights()

def plot_attention(
    self, plot: str = "time", output: str = "plot", width: int = 800, height: int = 400
):
    """
    Plot the attention weights.

    Args:
        plot (str, optional): The type of plot to generate. Can be one of the following:
            - 'time': Display the mean attention weights over time.
            - 'all': Display the attention weights for each horizon.
            - 'heatmap': Display the attention weights as a heatmap.
            - An integer in the range [1, model.h) to display the attention weights for a specific horizon.
        output (str, optional): The type of output to generate. Can be one of the following:
            - 'plot': Display the plot directly.
            - 'figure': Return the plot as a figure object.
        width (int, optional): Width of the plot in pixels. Default is 800.
        height (int, optional): Height of the plot in pixels. Default is 400.

    Returns:
        matplotlib.figure.Figure: If `output` is 'figure', the function returns the plot as a figure object.
    """

    attention = (
        self.mean_on_batch(self.interpretability_params["attn_wts"])
        .mean(dim=0)
        .cpu()
        .numpy()
    )

    fig, ax = plt.subplots(figsize=(width / 100, height / 100))

    if plot == "time":
        attention = attention[self.input_size :, :].mean(axis=0)
        ax.plot(np.arange(-self.input_size, self.h), attention)
        ax.axvline(
            x=0, color="black", linewidth=3, linestyle="--", label="prediction start"
        )
        ax.set_title("Mean Attention")
        ax.set_xlabel("time")
        ax.set_ylabel("Attention")
        ax.legend()

    elif plot == "all":
        for i in range(self.input_size, attention.shape[0]):
            ax.plot(
                np.arange(-self.input_size, self.h),
                attention[i, :],
                label=f"horizon {i-self.input_size+1}",
            )
        ax.axvline(
            x=0, color="black", linewidth=3, linestyle="--", label="prediction start"
        )
        ax.set_title("Attention per horizon")
        ax.set_xlabel("time")
        ax.set_ylabel("Attention")
        ax.legend()

    elif plot == "heatmap":
        cax = ax.imshow(
            attention,
            aspect="auto",
            cmap="viridis",
            extent=[-self.input_size, self.h, -self.input_size, self.h],
        )
        fig.colorbar(cax)
        ax.set_title("Attention Heatmap")
        ax.set_xlabel("Attention (current time step)")
        ax.set_ylabel("Attention (previous time step)")

    elif isinstance(plot, int) and (plot in np.arange(1, self.h + 1)):
        i = self.input_size + plot - 1
        ax.plot(
            np.arange(-self.input_size, self.h),
            attention[i, :],
            label=f"horizon {plot}",
        )
        ax.axvline(
            x=0, color="black", linewidth=3, linestyle="--", label="prediction start"
        )
        ax.set_title(f"Attention weight for horizon {plot}")
        ax.set_xlabel("time")
        ax.set_ylabel("Attention")
        ax.legend()

    else:
        raise ValueError(
            'plot has to be in ["time","all","heatmap"] or integer in range(1,model.h)'
        )

    plt.tight_layout()

    if output == "plot":
        plt.show()
    elif output == "figure":
        return fig
    else:
        raise ValueError(f"Invalid output: {output}. Expected 'plot' or 'figure'.")

3.1.1 Mean attention

plot_attention(nf.models[0], plot="time")

3.1.2 Attention of all future time steps

plot_attention(nf.models[0], plot="all")

3.1.3 Attention of a specific future time step

plot_attention(nf.models[0], plot=8)

3.2 Feature Importance

3.2.1 Global feature importance

feature_importances = nf.models[0].feature_importances()
feature_importances.keys()

Static variable importances

feature_importances["Static covariates"].sort_values(by="importance").plot(kind="barh")

Past variable importances

feature_importances["Past variable importance over time"].mean().sort_values().plot(
    kind="barh"
)

Future variable importances

feature_importances["Future variable importance over time"].mean().sort_values().plot(
    kind="barh"
)

3.2.2 Variable importances over time

Future variable importance over time

Importance of each future covariate at each future time step

df = feature_importances["Future variable importance over time"]


fig, ax = plt.subplots(figsize=(20, 10))
bottom = np.zeros(len(df.index))
for col in df.columns:
    p = ax.bar(np.arange(-len(df), 0), df[col].values, 0.6, label=col, bottom=bottom)
    bottom += df[col]
ax.set_title("Future variable importance over time ponderated by attention")
ax.set_ylabel("Importance")
ax.set_xlabel("Time")
ax.grid(True)
ax.legend()
plt.show()

Past variable importance over time

df = feature_importances["Past variable importance over time"]

fig, ax = plt.subplots(figsize=(20, 10))
bottom = np.zeros(len(df.index))

for col in df.columns:
    p = ax.bar(np.arange(-len(df), 0), df[col].values, 0.6, label=col, bottom=bottom)
    bottom += df[col]
ax.set_title("Past variable importance over time")
ax.set_ylabel("Importance")
ax.set_xlabel("Time")
ax.legend()
ax.grid(True)

plt.show()

Past variable importance over time ponderated by attention

Decomposition of the importance of each time step based on importance of each variable at that time step

df = feature_importances["Past variable importance over time"]
mean_attention = (
    nf.models[0]
    .attention_weights()[nf.models[0].input_size :, :]
    .mean(axis=0)[: nf.models[0].input_size]
)
df = df.multiply(mean_attention, axis=0)

fig, ax = plt.subplots(figsize=(20, 10))
bottom = np.zeros(len(df.index))

for col in df.columns:
    p = ax.bar(np.arange(-len(df), 0), df[col].values, 0.6, label=col, bottom=bottom)
    bottom += df[col]
ax.set_title("Past variable importance over time ponderated by attention")
ax.set_ylabel("Importance")
ax.set_xlabel("Time")
ax.legend()
ax.grid(True)
plt.plot(
    np.arange(-len(df), 0),
    mean_attention,
    color="black",
    marker="o",
    linestyle="-",
    linewidth=2,
    label="mean_attention",
)
plt.legend()
plt.show()

3.2.3 Variable importance correlations over time

Variables which gain and lose importance at same moments

nf.models[0].feature_importance_correlations()

4. Auxiliary Functions

4.1 Gating Mechanisms

The Gated Residual Network (GRN) provides adaptive depth and network complexity capable of accommodating different size datasets. As residual connections allow for the network to skip the non-linear transformation of input

\mathbf{a}

and context

\mathbf{c}

. The Gated Linear Unit (GLU) provides the flexibility of supressing unnecesary parts of the GRN. Consider GRN’s output

\gamma

then GLU transformation is defined by: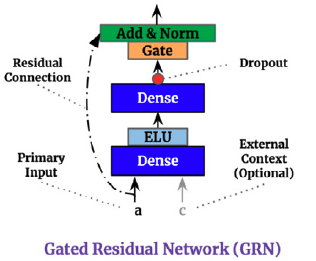

\mathrm{GLU}(\gamma) = \sigma(\mathbf{W}_{4}\gamma +b_{4}) \odot (\mathbf{W}_{5}\gamma +b_{5})

Figure 2. Gated Residual Network.

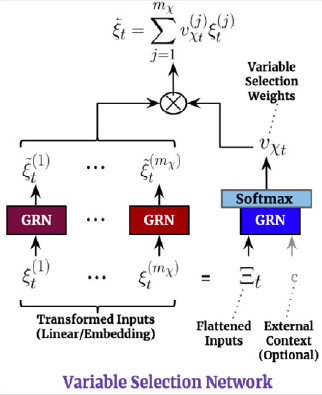
4.2 Variable Selection Networks

TFT includes automated variable selection capabilities, through its variable selection network (VSN) components. The VSN takes the original input

\{\mathbf{x}^{(s)}, \mathbf{x}^{(h)}_{[:t]}, \mathbf{x}^{(f)}_{[:t]}\}

and transforms it through embeddings or linear transformations into a high dimensional space

\{\mathbf{E}^{(s)}, \mathbf{E}^{(h)}_{[:t]}, \mathbf{E}^{(f)}_{[:t+H]}\}

. For the observed historic data, the embedding matrix

\mathbf{E}^{(h)}_{t}

at time

t

is a concatenation of

j

variable

e^{(h)}_{t,j}

embeddings: The variable selection weights are given by:

s^{(h)}_{t}=\mathrm{SoftMax}(\mathrm{GRN}(\mathbf{E}^{(h)}_{t},\mathbf{E}^{(s)}))

The VSN processed features are then:

\tilde{\mathbf{E}}^{(h)}_{t}= \sum_{j} s^{(h)}_{j} \tilde{e}^{(h)}_{t,j}

Figure 3. Variable Selection Network

4.3. Multi-Head Attention

To avoid information bottlenecks from the classic Seq2Seq architecture, TFT incorporates a decoder-encoder attention mechanism inherited transformer architectures (Li et. al 2019, Vaswani et. al 2017). It transform the the outputs of the LSTM encoded temporal features, and helps the decoder better capture long-term relationships. The original multihead attention for each component

H_{m}

and its query, key, and value representations are denoted by

Q_{m}, K_{m}, V_{m}

, its transformation is given by: TFT modifies the original multihead attention to improve its interpretability. To do it it uses shared values

\tilde{V}

across heads and employs additive aggregation,

\mathrm{InterpretableMultiHead}(Q,K,V) = \tilde{H} W_{M}

. The mechanism has a great resemblence to a single attention layer, but it allows for

M

multiple attention weights, and can be therefore be interpreted as the average ensemble of

M

single attention layers.

Getting Started

Capabilities

Tutorials

Use cases

API Reference

1. Temporal Fusion Decoder

`TFT`

`TFT.fit`

`TFT.predict`

`TFT.feature_importances`

`TFT.attention_weights`

`TFT.feature_importance_correlations`

Usage Example

2. TFT Architecture

2.1 Static Covariate Encoder

2.2 Temporal Covariate Encoder

2.3 Temporal Fusion Decoder

3. Interpretability

3.1 Attention Weights

3.1.1 Mean attention

3.1.2 Attention of all future time steps

3.1.3 Attention of a specific future time step

3.2 Feature Importance

3.2.1 Global feature importance

Static variable importances

Past variable importances

Future variable importances

3.2.2 Variable importances over time

Future variable importance over time

Past variable importance over time

Past variable importance over time ponderated by attention

3.2.3 Variable importance correlations over time

4. Auxiliary Functions

4.1 Gating Mechanisms

4.2 Variable Selection Networks

4.3. Multi-Head Attention

​1. Temporal Fusion Decoder

​TFT

​TFT.fit

​TFT.predict

​TFT.feature_importances

​TFT.attention_weights

​TFT.feature_importance_correlations

​Usage Example

​2. TFT Architecture

​2.1 Static Covariate Encoder

​2.2 Temporal Covariate Encoder

​2.3 Temporal Fusion Decoder

​3. Interpretability

​3.1 Attention Weights

3.1.1 Mean attention

3.1.2 Attention of all future time steps

3.1.3 Attention of a specific future time step

​3.2 Feature Importance

​3.2.1 Global feature importance

Static variable importances

Past variable importances

Future variable importances

​3.2.2 Variable importances over time

Future variable importance over time

Past variable importance over time

Past variable importance over time ponderated by attention

​3.2.3 Variable importance correlations over time

​4. Auxiliary Functions

​4.1 Gating Mechanisms

​4.2 Variable Selection Networks

​4.3. Multi-Head Attention

1. Temporal Fusion Decoder

`TFT`

`TFT.fit`

`TFT.predict`

`TFT.feature_importances`

`TFT.attention_weights`

`TFT.feature_importance_correlations`

Usage Example

2. TFT Architecture

2.1 Static Covariate Encoder

2.2 Temporal Covariate Encoder

2.3 Temporal Fusion Decoder

3. Interpretability

3.1 Attention Weights

3.2 Feature Importance

3.2.1 Global feature importance

3.2.2 Variable importances over time

3.2.3 Variable importance correlations over time

4. Auxiliary Functions

4.1 Gating Mechanisms

4.2 Variable Selection Networks

4.3. Multi-Head Attention