Predictive maintenance (PdM) is a data-driven preventive maintanance program. It is a proactive maintenance strategy that uses sensors to monitor the performance and equipment conditions during operation. The PdM methods constantly analyze the data to predict when optimal maintenance schedules. It can reduce maintenance costs and prevent catastrophic equipment failure when used correctly. In this notebook, we will apply NeuralForecast to perform a supervised Remaining Useful Life (RUL) estimation on the classic PHM2008 aircraft degradation dataset. Outline
1. Installing Packages
2. Load PHM2008 aircraft degradation dataset
3. Fit and Predict NeuralForecast
4. Evaluate Predictions You can run these experiments using GPU with Google Colab. Open In Colab

​
1. Installing Packages

!pip install neuralforecast datasetsforecast

import logging
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'serif'

from neuralforecast.models import NBEATSx
from neuralforecast import NeuralForecast
from neuralforecast.losses.pytorch import HuberLoss

from datasetsforecast.phm2008 import PHM2008

logging.getLogger("pytorch_lightning").setLevel(logging.ERROR)

​
2. Load PHM2008 aircraft degradation dataset

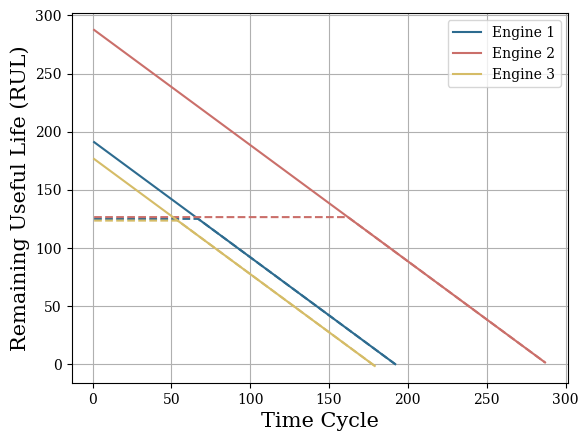
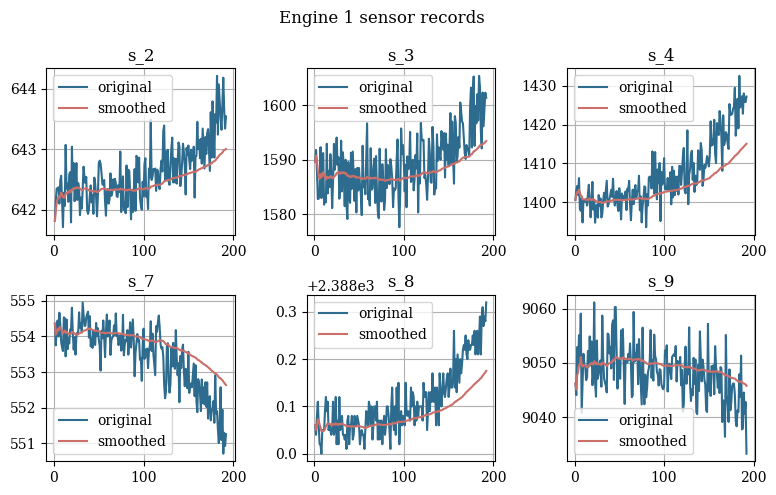
Here we will load the Prognosis and Health Management 2008 challenge dataset. This dataset used the Commercial Modular Aero-Propulsion System Simulation to recreate the degradation process of turbofan engines for different aircraft with varying wear and manufacturing starting under normal conditions. The training dataset consists of complete run-to-failure simulations, while the test dataset comprises sequences before failure. 
Y_train_df, Y_test_df = PHM2008.load(directory='./data', group='FD001', clip_rul=False)
Y_train_df

100%|██████████| 12.4M/12.4M [00:00<00:00, 21.6MiB/s]
INFO:datasetsforecast.utils:Successfully downloaded CMAPSSData.zip, 12437405, bytes.
INFO:datasetsforecast.utils:Decompressing zip file...
INFO:datasetsforecast.utils:Successfully decompressed data\phm2008\CMAPSSData.zip
unique_iddss_2s_3s_4s_7s_8s_9s_11s_12s_13s_14s_15s_17s_20s_21y
011641.821589.701400.60554.362388.069046.1947.47521.662388.028138.628.419539239.0623.4190191
112642.151591.821403.14553.752388.049044.0747.49522.282388.078131.498.431839239.0023.4236190
213642.351587.991404.20554.262388.089052.9447.27522.422388.038133.238.417839038.9523.3442189
314642.351582.791401.87554.452388.119049.4847.13522.862388.088133.838.368239238.8823.3739188
415642.371582.851406.22554.002388.069055.1547.28522.192388.048133.808.429439338.9023.4044187
………………………………………………
20626100196643.491597.981428.63551.432388.199065.5248.07519.492388.268137.608.495639738.4922.97354
20627100197643.541604.501433.58550.862388.239065.1148.04519.682388.228136.508.513939538.3023.15943
20628100198643.421602.461428.18550.942388.249065.9048.09520.012388.248141.058.564639838.4422.93332
20629100199643.231605.261426.53550.682388.259073.7248.39519.672388.238139.298.538939538.2923.06401
20630100200643.851600.381432.14550.792388.269061.4848.20519.302388.268137.338.503639638.3723.05220
plot_df1 = Y_train_df[Y_train_df['unique_id']==1]
plot_df2 = Y_train_df[Y_train_df['unique_id']==2]
plot_df3 = Y_train_df[Y_train_df['unique_id']==3]

plt.plot(plot_df1.ds, np.minimum(plot_df1.y, 125), color='#2D6B8F', linestyle='--')
plt.plot(plot_df1.ds, plot_df1.y, color='#2D6B8F', label='Engine 1')

plt.plot(plot_df2.ds, np.minimum(plot_df2.y, 125)+1.5, color='#CA6F6A', linestyle='--')
plt.plot(plot_df2.ds, plot_df2.y+1.5, color='#CA6F6A', label='Engine 2')

plt.plot(plot_df3.ds, np.minimum(plot_df3.y, 125)-1.5, color='#D5BC67', linestyle='--')
plt.plot(plot_df3.ds, plot_df3.y-1.5, color='#D5BC67', label='Engine 3')

plt.ylabel('Remaining Useful Life (RUL)', fontsize=15)
plt.xlabel('Time Cycle', fontsize=15)
plt.legend()
plt.grid()

def smooth(s, b = 0.98):
    v = np.zeros(len(s)+1) #v_0 is already 0.
    bc = np.zeros(len(s)+1)
    for i in range(1, len(v)): #v_t = 0.95
        v[i] = (b * v[i-1] + (1-b) * s[i-1]) 
        bc[i] = 1 - b**i
    sm = v[1:] / bc[1:]
    return sm

unique_id = 1
plot_df = Y_train_df[Y_train_df.unique_id == unique_id].copy()

fig, axes = plt.subplots(2,3, figsize = (8,5))
fig.tight_layout()

j = -1
#, 's_11', 's_12', 's_13', 's_14', 's_15', 's_17', 's_20', 's_21'
for feature in ['s_2', 's_3', 's_4', 's_7', 's_8', 's_9']:
    if ('s' in feature) and ('smoothed' not in feature):
        j += 1
        axes[j // 3, j % 3].plot(plot_df.ds, plot_df[feature], 
                                 c = '#2D6B8F', label = 'original')
        axes[j // 3, j % 3].plot(plot_df.ds, smooth(plot_df[feature].values), 
                                 c = '#CA6F6A', label = 'smoothed')
        #axes[j // 3, j % 3].plot([10,10],[0,1], c = 'black')
        axes[j // 3, j % 3].set_title(feature)
        axes[j // 3, j % 3].grid()
        axes[j // 3, j % 3].legend()
        
plt.suptitle(f'Engine {unique_id} sensor records')
plt.tight_layout()

​
3. Fit and Predict NeuralForecast

NeuralForecast methods are capable of addressing regression problems involving various variables. The regression problem involves predicting the target variable yt+hy_{t+h} based on its lags y:ty_{:t}, temporal exogenous features x:t(h)x^{(h)}_{:t}, exogenous features available at the time of prediction x:t+h(f)x^{(f)}_{:t+h}, and static features x(s)x^{(s)}. The task of estimating the remaining useful life (RUL) simplifies the problem to a single horizon prediction h=1h=1, where the objective is to predict yt+1y_{t+1} based on the exogenous features x:t+1(f)x^{(f)}_{:t+1} and static features x(s)x^{(s)}. In the RUL estimation task, the exogenous features typically correspond to sensor monitoring information, while the target variable represents the RUL itself. P(yt+1  ∣  x:t+1(f),x(s))P(y_{t+1}\;|\;x^{(f)}_{:t+1},x^{(s)}) 
Y_train_df, Y_test_df = PHM2008.load(directory='./data', group='FD001', clip_rul=True)
max_ds = Y_train_df.groupby('unique_id')["ds"].max()
Y_test_df = Y_test_df.merge(max_ds, on='unique_id', how='left', suffixes=('', '_train_max_date'))
Y_test_df["ds"] = Y_test_df["ds"] + Y_test_df["ds_train_max_date"]
Y_test_df = Y_test_df.drop(columns=["ds_train_max_date"])

futr_exog_list =['s_2', 's_3', 's_4', 's_7', 's_8', 's_9', 's_11',
                 's_12', 's_13', 's_14', 's_15', 's_17', 's_20', 's_21']

model = NBEATSx(h=1, 
                input_size=24,
                loss=HuberLoss(),
                scaler_type='robust',
                stack_types=['identity', 'identity', 'identity'],
                dropout_prob_theta=0.5,
                futr_exog_list=futr_exog_list,
                exclude_insample_y = True,
                max_steps=1000)
nf = NeuralForecast(models=[model], freq=1)

nf.fit(df=Y_train_df)
Y_hat_df = nf.predict(futr_df=Y_test_df)

​
4. Evaluate Predictions

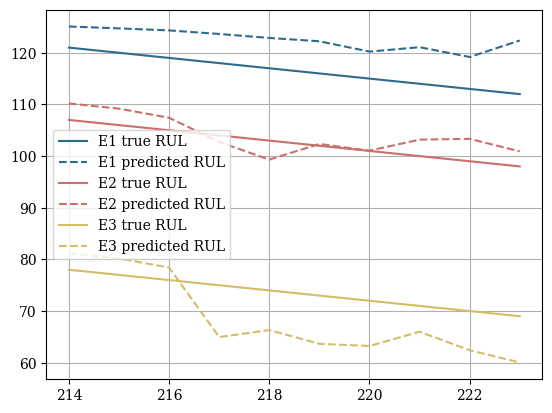
In the original PHM2008 dataset the true RUL values for the test set are only provided for the last time cycle of each enginge. We will filter the predictions to only evaluate the last time cycle. RMSE(yT,y^T)=1∣Dtest∣∑i(yi,T−y^i,T)2RMSE(\mathbf{y}_{T},\hat{\mathbf{y}}_{T}) = \sqrt{\frac{1}{|\mathcal{D}_{test}|} \sum_{i} (y_{i,T}-\hat{y}_{i,T})^{2}} 
from utilsforecast.evaluation import evaluate
from utilsforecast.losses import rmse

metrics = evaluate(Y_hat_df.merge(Y_test_df[["unique_id", "ds", "y"]], on=['unique_id', 'ds']),
                   metrics=[rmse],
                   agg_fn='mean')

metrics
metricNBEATSx
0rmse118.179373
plot_df1 = Y_hat_df2[Y_hat_df2['unique_id']==1]
plot_df2 = Y_hat_df2[Y_hat_df2['unique_id']==2]
plot_df3 = Y_hat_df2[Y_hat_df2['unique_id']==3]

plt.plot(plot_df1.ds, plot_df1['y'], c='#2D6B8F', label='E1 true RUL')
plt.plot(plot_df1.ds, plot_df1[model_name]+1, c='#2D6B8F', linestyle='--', label='E1 predicted RUL')

plt.plot(plot_df1.ds, plot_df2['y'], c='#CA6F6A', label='E2 true RUL')
plt.plot(plot_df1.ds, plot_df2[model_name]+1, c='#CA6F6A', linestyle='--', label='E2 predicted RUL')

plt.plot(plot_df1.ds, plot_df3['y'], c='#D5BC67', label='E3 true RUL')
plt.plot(plot_df1.ds, plot_df3[model_name]+1, c='#D5BC67', linestyle='--', label='E3 predicted RUL')

plt.legend()
plt.grid()

​
References