Skip to main content
The Hierarchical Mixture Networks (HINT) are a highly modular framework that combines SoTA neural forecast architectures with task-specialized mixture probability and advanced hierarchical reconciliation strategies. This powerful combination allows HINT to produce accurate and coherent probabilistic forecasts. HINT’s incorporates a TemporalNorm module into any neural forecast architecture, the module normalizes inputs into the network’s non-linearities operating range and recomposes its output’s scales through a global skip connection, improving accuracy and training robustness. HINT ensures the forecast coherence via bootstrap sample reconciliation that restores the aggregation constraints into its base samples. References Figure 1. Hierarchical Mixture Networks (HINT). Figure 1. Hierarchical Mixture Networks (HINT).

​
1. HINT

​
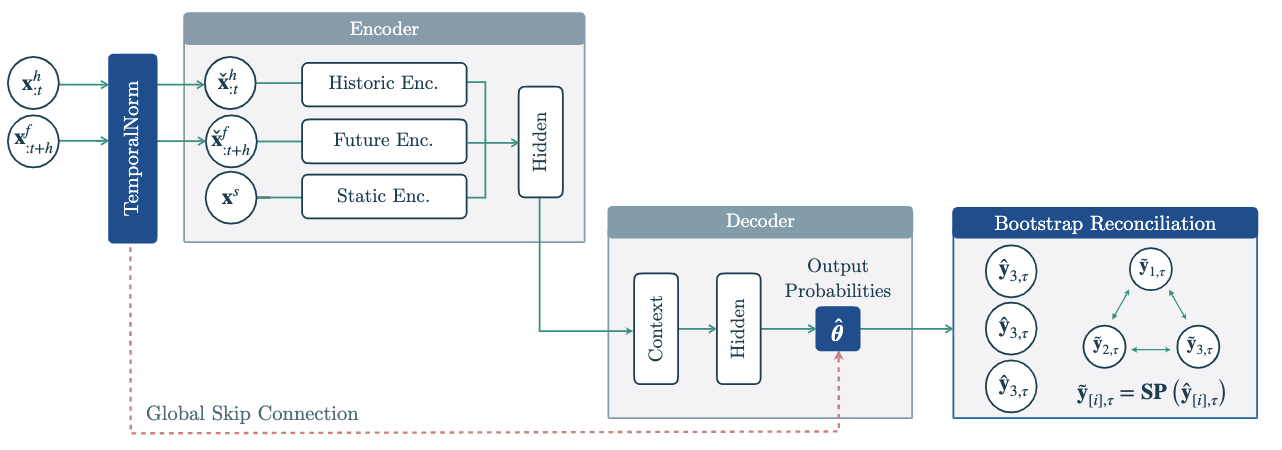
HINT

HINT(h, S, model, reconciliation, alias=None)
HINT The Hierarchical Mixture Networks (HINT) are a highly modular framework that combines SoTA neural forecast architectures with a task-specialized mixture probability and advanced hierarchical reconciliation strategies. This powerful combination allows HINT to produce accurate and coherent probabilistic forecasts. HINT’s incorporates a TemporalNorm module into any neural forecast architecture, the module normalizes inputs into the network’s non-linearities operating range and recomposes its output’s scales through a global skip connection, improving accuracy and training robustness. HINT ensures the forecast coherence via bootstrap sample reconciliation that restores the aggregation constraints into its base samples.
  • Identity
Parameters:
NameTypeDescriptionDefault
hintForecast horizon.required
modelNeuralForecast modelInstantiated model class from architecture collection.required
SndarrayDumming matrix of size (base, bottom) see HierarchicalForecast’s aggregate method.required
reconciliationstrHINT’s reconciliation method from [‘BottomUp’, ‘MinTraceOLS’, ‘MinTraceWLS’].required
aliasstrCustom name of the model.None

​
HINT.fit

fit(
    dataset, val_size=0, test_size=0, random_seed=None, distributed_config=None
)
HINT.fit HINT trains on the entire hierarchical dataset, by minimizing a composite log likelihood objective. HINT framework integrates TemporalNorm into the neural forecast architecture for a scale-decoupled optimization that robustifies cross-learning the hierachy’s series scales. Parameters:
NameTypeDescriptionDefault
datasetTimeSeriesDatasetNeuralForecast’s TimeSeriesDataset see details hererequired
val_sizeintsize of the validation set, (default 0).0
test_sizeintsize of the test set, (default 0).0
random_seedintrandom seed for the prediction.None
Returns:
NameTypeDescription
selfA fitted base NeuralForecast model.

​
HINT.predict

predict(dataset, step_size=1, random_seed=None, **data_module_kwargs)
HINT.predict After fitting a base model on the entire hierarchical dataset. HINT restores the hierarchical aggregation constraints using bootstrapped sample reconciliation. Parameters:
NameTypeDescriptionDefault
datasetTimeSeriesDatasetNeuralForecast’s TimeSeriesDataset see details hererequired
step_sizeintsteps between sequential predictions, (default 1).1
random_seedintrandom seed for the prediction.None
**data_kwargadditional parameters for the dataset module.required
Returns:
NameTypeDescription
y_hatnumpy predictions of the NeuralForecast model.

​
Usage Example

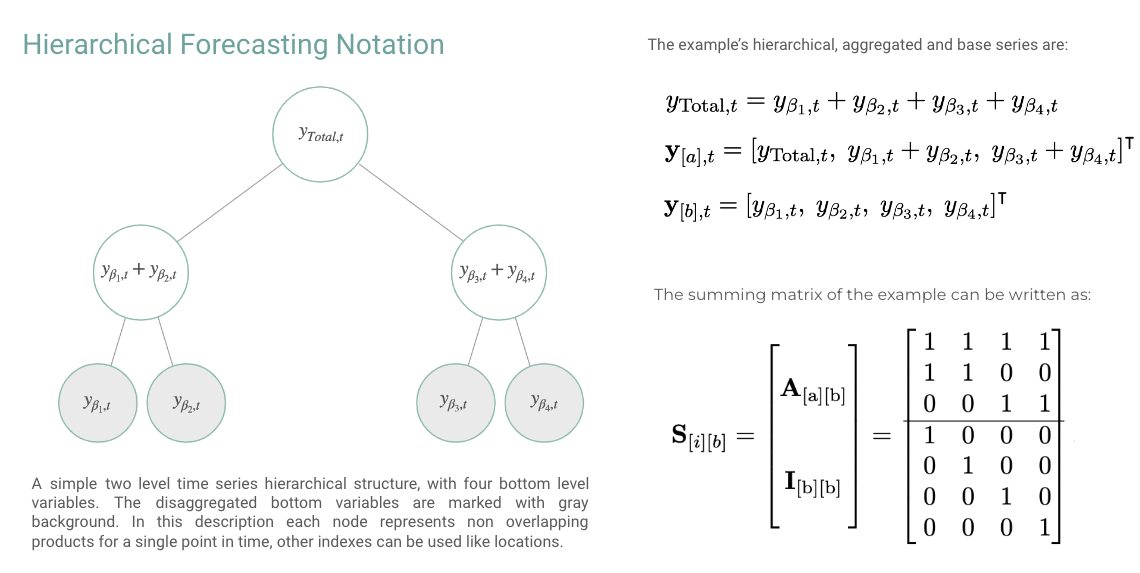
In this example we will use HINT for the hierarchical forecast task, a multivariate regression problem with aggregation constraints. The aggregation constraints can be compactcly represented by the summing matrix S[i][b]\mathbf{S}_{[i][b]}, the Figure belows shows an example. In this example we will make coherent predictions for the TourismL dataset. Outline:
  1. Import packages
  2. Load hierarchical dataset
  3. Fit and Predict HINT
  4. Forecast Plot
import matplotlib.pyplot as plt

from neuralforecast.losses.pytorch import GMM, sCRPS
from datasetsforecast.hierarchical import HierarchicalData

# Auxiliary sorting
def sort_df_hier(Y_df, S_df):
    # NeuralForecast core, sorts unique_id lexicographically
    # by default, this class matches S_df and Y_hat_df order.    
    Y_df.unique_id = Y_df.unique_id.astype('category')
    Y_df.unique_id = Y_df.unique_id.cat.set_categories(S_df.index)
    Y_df = Y_df.sort_values(by=['unique_id', 'ds'])
    return Y_df

# Load TourismSmall dataset
horizon = 12
Y_df, S_df, tags = HierarchicalData.load('./data', 'TourismLarge')
Y_df['ds'] = pd.to_datetime(Y_df['ds'])
Y_df = sort_df_hier(Y_df, S_df)
level = [80,90]

# Instantiate HINT
# BaseNetwork + Distribution + Reconciliation
nhits = NHITS(h=horizon,
              input_size=24,
              loss=GMM(n_components=10, level=level),
              max_steps=2000,
              early_stop_patience_steps=10,
              val_check_steps=50,
              scaler_type='robust',
              learning_rate=1e-3,
              valid_loss=sCRPS(level=level))

model = HINT(h=horizon, S=S_df.values,
             model=nhits,  reconciliation='BottomUp')

# Fit and Predict
nf = NeuralForecast(models=[model], freq='MS')
Y_hat_df = nf.cross_validation(df=Y_df, val_size=12, n_windows=1)
Y_hat_df = Y_hat_df.reset_index()

# Plot coherent probabilistic forecast
unique_id = 'TotalAll'
Y_plot_df = Y_df[Y_df.unique_id==unique_id]
plot_df = Y_hat_df[Y_hat_df.unique_id==unique_id]
plot_df = Y_plot_df.merge(plot_df, on=['ds', 'unique_id'], how='left')
n_years = 5

plt.plot(plot_df['ds'][-12*n_years:], plot_df['y_x'][-12*n_years:], c='black', label='True')
plt.plot(plot_df['ds'][-12*n_years:], plot_df['HINT'][-12*n_years:], c='purple', label='mean')
plt.plot(plot_df['ds'][-12*n_years:], plot_df['HINT-median'][-12*n_years:], c='blue', label='median')
plt.fill_between(x=plot_df['ds'][-12*n_years:],
                 y1=plot_df['HINT-lo-90'][-12*n_years:].values,
                 y2=plot_df['HINT-hi-90'][-12*n_years:].values,
                 alpha=0.4, label='level 90')
plt.legend()
plt.grid()
plt.plot()

​
2. Reconciliation Methods

​
get_identity_P

get_identity_P(S)

​
get_bottomup_P

get_bottomup_P(S)
BottomUp Reconciliation Matrix. Creates BottomUp hierarchical “projection” matrix is defined as: PBU=[0[b],[a]  ∣  I[b][b]]\mathbf{P}_{\text{BU}} = [\mathbf{0}_{\mathrm{[b],[a]}}\;|\;\mathbf{I}_{\mathrm{[b][b]}}] Parameters:
NameTypeDescriptionDefault
SndarraySumming matrix of size (base, bottom).required
Returns:
TypeDescription
np.ndarray: Reconciliation matrix of size (bottom, base).

​
get_mintrace_ols_P

get_mintrace_ols_P(S)
MinTraceOLS Reconciliation Matrix. Creates MinTraceOLS reconciliation matrix as proposed by Wickramasuriya et al. PMinTraceOLS=(S⊺S)−1S⊺\mathbf{P}_{\text{MinTraceOLS}}=\left(\mathbf{S}^{\intercal}\mathbf{S}\right)^{-1}\mathbf{S}^{\intercal} Parameters:
NameTypeDescriptionDefault
SndarraySumming matrix of size (base, bottom).required
Returns:
TypeDescription
np.ndarray: Reconciliation matrix of size (bottom, base).

​
get_mintrace_wls_P

get_mintrace_wls_P(S)
MinTraceOLS Reconciliation Matrix. Creates MinTraceOLS reconciliation matrix as proposed by Wickramasuriya et al. Depending on a weighted GLS estimator and an estimator of the covariance matrix of the coherency errors mathbfW_h\\mathbf{W}\_{h}. Wh=Diag(S1[b])\mathbf{W}_{h} = \mathrm{Diag}(\mathbf{S} \mathbb{1}_{[b]}) PMinTraceWLS=(S⊺WhS)−1S⊺Wh−1\mathbf{P}_{\text{MinTraceWLS}}=\left(\mathbf{S}^{\intercal}\mathbf{W}_{h}\mathbf{S}\right)^{-1} \mathbf{S}^{\intercal}\mathbf{W}^{-1}_{h} Parameters:
NameTypeDescriptionDefault
SndarraySumming matrix of size (base, bottom).required
Returns:
TypeDescription
np.ndarray: Reconciliation matrix of size (bottom, base).