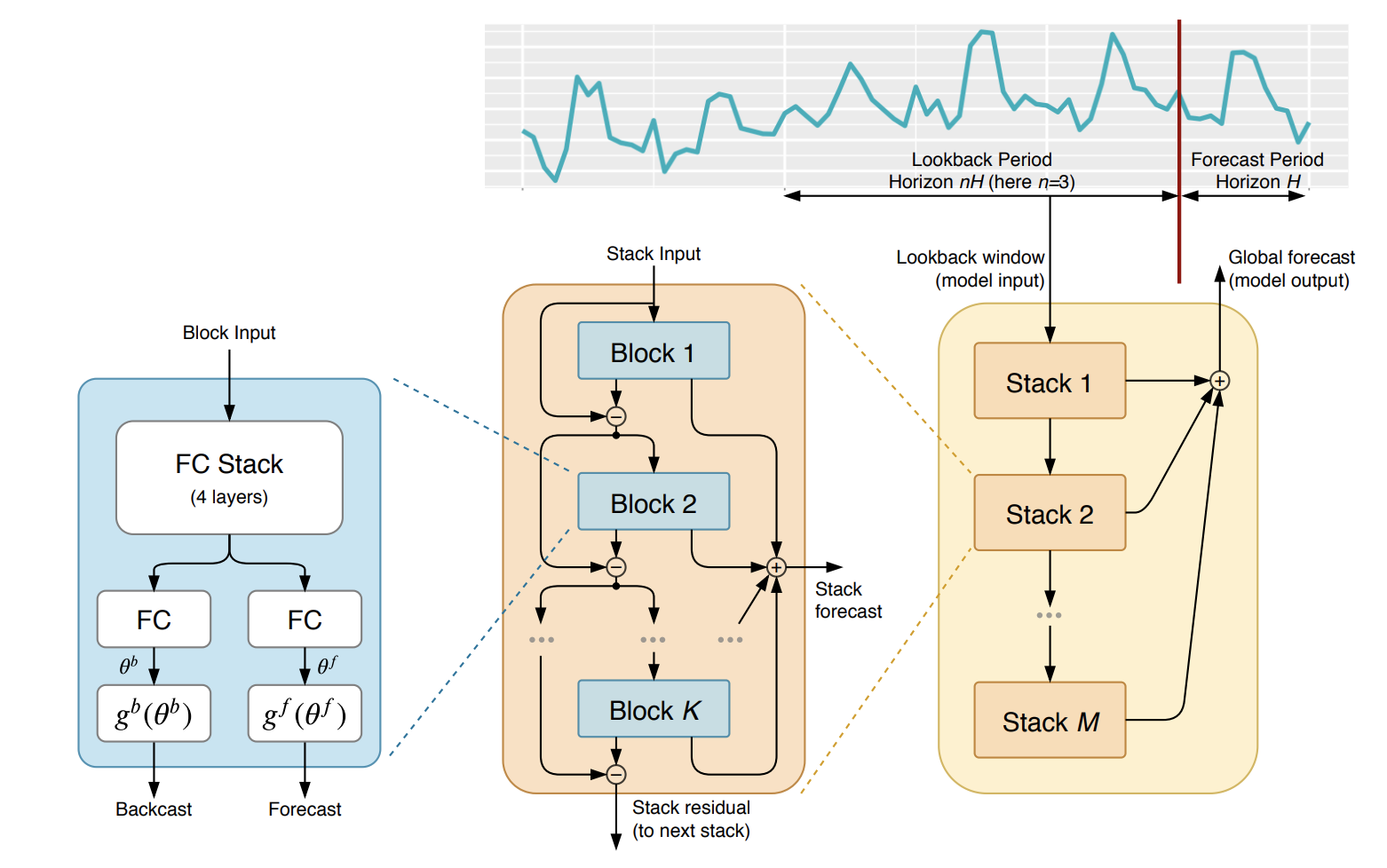
NBEATS) is an
MLP-based
deep neural architecture with backward and forward residual links. The
network has two variants: (1) in its interpretable configuration,
NBEATS
sequentially projects the signal into polynomials and harmonic basis to
learn trend and seasonality components; (2) in its generic
configuration, it substitutes the polynomial and harmonic basis for
identity basis and larger network’s depth. The Neural Basis Expansion
Analysis with Exogenous
(NBEATSx),
incorporates projections to exogenous temporal variables available at
the time of the prediction.
This method proved state-of-the-art performance on the M3, M4, and
Tourism Competition datasets, improving accuracy by 3% over the ESRNN
M4 competition winner.
References
NBEATS
NBEATS
BaseModel
NBEATS
The Neural Basis Expansion Analysis for Time Series (NBEATS), is a simple and yet
effective architecture, it is built with a deep stack of MLPs with the doubly
residual connections. It has a generic and interpretable architecture depending
on the blocks it uses. Its interpretable architecture is recommended for scarce
data settings, as it regularizes its predictions through projections unto harmonic
and trend basis well-suited for most forecasting tasks.
Parameters:
h: int, forecast horizon.
input_size: int, considered autorregresive inputs (lags), y=[1,2,3,4] input_size=2 -> lags=[1,2].
n_harmonics: int, Number of harmonic terms for seasonality stack type. Note that len(n_harmonics) = len(stack_types). Note that it will only be used if a seasonality stack is used.
n_polynomials: int, DEPRECATED - polynomial degree for trend stack. Note that len(n_polynomials) = len(stack_types). Note that it will only be used if a trend stack is used.
basis: str, Type of basis function to use in the trend stack. Choose one from [‘legendre’, ‘polynomial’, ‘changepoint’, ‘piecewise_linear’, ‘linear_hat’, ‘spline’, ‘chebyshev’]
n_basis: int, the degree of the basis function for the trend stack. Note that it will only be used if a trend stack is used.
stack_types: List[str], List of stack types. Subset from [‘seasonality’, ‘trend’, ‘identity’].
n_blocks: List[int], Number of blocks for each stack. Note that len(n_blocks) = len(stack_types).
mlp_units: List[List[int]], Structure of hidden layers for each stack type. Each internal list should contain the number of units of each hidden layer. Note that len(n_hidden) = len(stack_types).
dropout_prob_theta: float, Float between (0, 1). Dropout for N-BEATS basis.
activation: str, activation from [‘ReLU’, ‘Softplus’, ‘Tanh’, ‘SELU’, ‘LeakyReLU’, ‘PReLU’, ‘Sigmoid’].
shared_weights: bool, If True, all blocks within each stack will share parameters.
loss: PyTorch module, instantiated train loss class from losses collection.
valid_loss: PyTorch module=loss, instantiated valid loss class from losses collection.
max_steps: int=1000, maximum number of training steps.
learning_rate: float=1e-3, Learning rate between (0, 1).
num_lr_decays: int=3, Number of learning rate decays, evenly distributed across max_steps.
early_stop_patience_steps: int=-1, Number of validation iterations before early stopping.
val_check_steps: int=100, Number of training steps between every validation loss check.
batch_size: int=32, number of different series in each batch.
valid_batch_size: int=None, number of different series in each validation and test batch, if None uses batch_size.
windows_batch_size: int=1024, number of windows to sample in each training batch, default uses all.
inference_windows_batch_size: int=-1, number of windows to sample in each inference batch, -1 uses all.
start_padding_enabled: bool=False, if True, the model will pad the time series with zeros at the beginning, by input size.
training_data_availability_threshold: Union[float, List[float]]=0.0, minimum fraction of valid data points required for training windows. Single float applies to both insample and outsample; list of two floats specifies [insample_fraction, outsample_fraction]. Default 0.0 allows windows with only 1 valid data point (current behavior).
step_size: int=1, step size between each window of temporal data.
scaler_type: str=‘identity’, type of scaler for temporal inputs normalization see temporal scalers.
random_seed: int, random_seed for pytorch initializer and numpy generators.
drop_last_loader: bool=False, if True TimeSeriesDataLoader drops last non-full batch.
alias: str, optional, Custom name of the model.
optimizer: Subclass of ‘torch.optim.Optimizer’, optional, user specified optimizer instead of the default choice (Adam).
optimizer_kwargs: dict, optional, list of parameters used by the user specified optimizer.
lr_scheduler: Subclass of ‘torch.optim.lr_scheduler.LRScheduler’, optional, user specified lr_scheduler instead of the default choice (StepLR).
lr_scheduler_kwargs: dict, optional, list of parameters used by the user specified lr_scheduler.
dataloader_kwargs: dict, optional, list of parameters passed into the PyTorch Lightning dataloader by the TimeSeriesDataLoader.
**trainer_kwargs: int, keyword trainer arguments inherited from PyTorch Lighning’s trainer.
References:
-Boris N. Oreshkin, Dmitri Carpov, Nicolas Chapados, Yoshua Bengio (2019).
“N-BEATS: Neural basis expansion analysis for interpretable time series forecasting”.
NBEATS.fit
fit method, optimizes the neural network’s weights using the
initialization parameters (learning_rate, windows_batch_size, …)
and the loss function as defined during the initialization.
Within fit we use a PyTorch Lightning Trainer that
inherits the initialization’s self.trainer_kwargs, to customize
its inputs, see PL’s trainer arguments.
The method is designed to be compatible with SKLearn-like classes
and in particular to be compatible with the StatsForecast library.
By default the model is not saving training checkpoints to protect
disk memory, to get them change enable_checkpointing=True in __init__.
Parameters:
| Name | Type | Description | Default |
|---|---|---|---|
dataset | TimeSeriesDataset | NeuralForecast’s TimeSeriesDataset, see documentation. | required |
val_size | int | Validation size for temporal cross-validation. | 0 |
random_seed | int | Random seed for pytorch initializer and numpy generators, overwrites model.init’s. | None |
test_size | int | Test size for temporal cross-validation. | 0 |
| Type | Description |
|---|---|
| None |
NBEATS.predict
Trainer execution of predict_step.
Parameters:
| Name | Type | Description | Default |
|---|---|---|---|
dataset | TimeSeriesDataset | NeuralForecast’s TimeSeriesDataset, see documentation. | required |
test_size | int | Test size for temporal cross-validation. | None |
step_size | int | Step size between each window. | 1 |
random_seed | int | Random seed for pytorch initializer and numpy generators, overwrites model.init’s. | None |
quantiles | list | Target quantiles to predict. | None |
h | int | Prediction horizon, if None, uses the model’s fitted horizon. Defaults to None. | None |
explainer_config | dict | configuration for explanations. | None |
**data_module_kwargs | dict | PL’s TimeSeriesDataModule args, see documentation. |
| Type | Description |
|---|---|
| None |

