Skip to main content
Long-horizon forecasting is challenging because of the volatility of the predictions and the computational complexity. To solve this problem we created the Neural Hierarchical Interpolation for Time Series (NHITS). NHITS builds upon NBEATS and specializes its partial outputs in the different frequencies of the time series through hierarchical interpolation and multi-rate input processing. On the long-horizon forecasting task NHITS improved accuracy by 25% on AAAI’s best paper award the Informer, while being 50x faster. 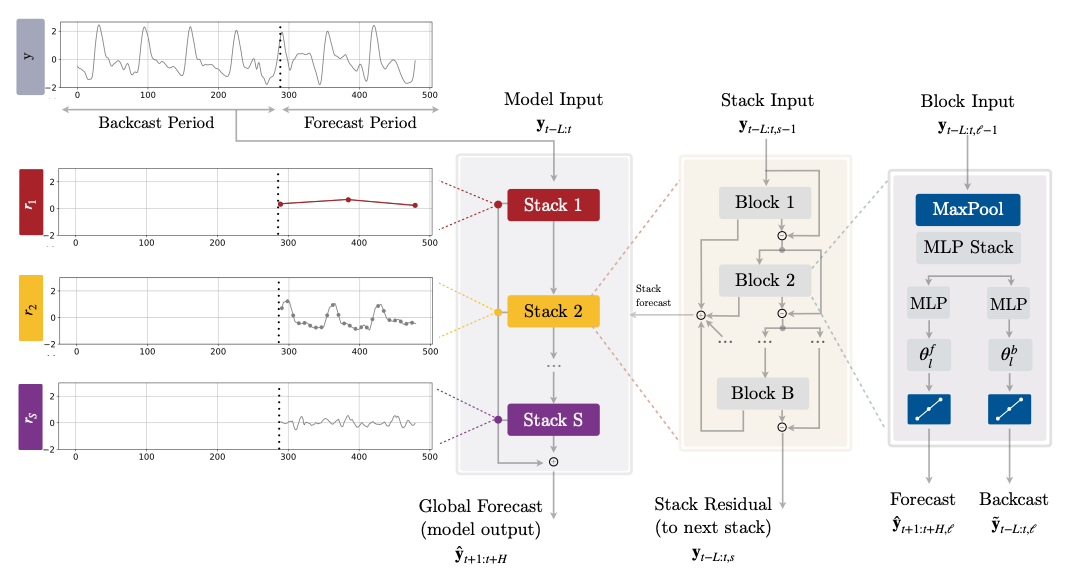The model is composed of several MLPs with ReLU non-linearities. Blocks are connected via doubly residual stacking principle with the backcast y~t−L:t,l\mathbf{\tilde{y}}_{t-L:t,l} and forecast y^t+1:t+H,l\mathbf{\hat{y}}_{t+1:t+H,l} outputs of the l-th block. Multi-rate input pooling, hierarchical interpolation and backcast residual connections together induce the specialization of the additive predictions in different signal bands, reducing memory footprint and computational time, thus improving the architecture parsimony and accuracy. References Figure 1. Neural Hierarchical Interpolation for Time Series (NHITS). Figure 1. Neural Hierarchical Interpolation for Time Series (NHITS).

​
NHITS

​
NHITS

NHITS(
    h,
    input_size,
    futr_exog_list=None,
    hist_exog_list=None,
    stat_exog_list=None,
    exclude_insample_y=False,
    stack_types=["identity", "identity", "identity"],
    n_blocks=[1, 1, 1],
    mlp_units=3 * [[512, 512]],
    n_pool_kernel_size=[2, 2, 1],
    n_freq_downsample=[4, 2, 1],
    pooling_mode="MaxPool1d",
    interpolation_mode="linear",
    dropout_prob_theta=0.0,
    activation="ReLU",
    loss=MAE(),
    valid_loss=None,
    max_steps=1000,
    learning_rate=0.001,
    num_lr_decays=3,
    early_stop_patience_steps=-1,
    val_monitor="ptl/val_loss",
    val_check_steps=100,
    batch_size=32,
    valid_batch_size=None,
    windows_batch_size=1024,
    inference_windows_batch_size=-1,
    start_padding_enabled=False,
    training_data_availability_threshold=0.0,
    step_size=1,
    scaler_type="identity",
    random_seed=1,
    drop_last_loader=False,
    alias=None,
    optimizer=None,
    optimizer_kwargs=None,
    lr_scheduler=None,
    lr_scheduler_kwargs=None,
    dataloader_kwargs=None,
    **trainer_kwargs
)
Bases: BaseModel NHITS The Neural Hierarchical Interpolation for Time Series (NHITS), is an MLP-based deep neural architecture with backward and forward residual links. NHITS tackles volatility and memory complexity challenges, by locally specializing its sequential predictions into the signals frequencies with hierarchical interpolation and pooling. Parameters:
NameTypeDescriptionDefault
hintForecast horizon.required
input_sizeintautorregresive inputs size, y=[1,2,3,4] input_size=2 -> y_[t-2:t]=[1,2].required
futr_exog_liststr listfuture exogenous columns.None
hist_exog_liststr listhistoric exogenous columns.None
stat_exog_liststr liststatic exogenous columns.None
exclude_insample_yboolthe model skips the autoregressive features y[t-input_size:t] if True.False
stack_typesList[str]stacks list in the form N * [‘identity’], to be deprecated in favor of n_stacks. Note that len(stack_types)=len(n_freq_downsample)=len(n_pool_kernel_size).[‘identity’, ‘identity’, ‘identity’]
n_blocksList[int]Number of blocks for each stack. Note that len(n_blocks) = len(stack_types).[1, 1, 1]
mlp_unitsList[List[int]]Structure of hidden layers for each stack type. Each internal list should contain the number of units of each hidden layer. Note that len(n_hidden) = len(stack_types).3 * [[512, 512]]
n_pool_kernel_sizeList[int]list with the size of the windows to take a max/avg over. Note that len(stack_types)=len(n_freq_downsample)=len(n_pool_kernel_size).[2, 2, 1]
n_freq_downsampleList[int]list with the stack’s coefficients (inverse expressivity ratios). Note that len(stack_types)=len(n_freq_downsample)=len(n_pool_kernel_size).[4, 2, 1]
pooling_modestrinput pooling module from [‘MaxPool1d’, ‘AvgPool1d’].’MaxPool1d’
interpolation_modestrinterpolation basis from [‘linear’, ‘nearest’, ‘cubic’].‘linear’
dropout_prob_thetafloatFloat between (0, 1). Dropout for NHITS basis.0.0
activationstractivation from [‘ReLU’, ‘Softplus’, ‘Tanh’, ‘SELU’, ‘LeakyReLU’, ‘PReLU’, ‘Sigmoid’].’ReLU’
learning_ratefloatLearning rate between (0, 1).0.001
num_lr_decaysintNumber of learning rate decays, evenly distributed across max_steps.3
early_stop_patience_stepsintNumber of validation iterations before early stopping.-1
val_monitorstrmetric to monitor for early stopping. Valid options: “ptl/val_loss”, “valid_loss”, “train_loss”. Default: “ptl/val_loss”.‘ptl/val_loss’
val_check_stepsintNumber of training steps between every validation loss check.100
batch_sizeintnumber of different series in each batch.32
valid_batch_sizeintnumber of different series in each validation and test batch, if None uses batch_size.None
windows_batch_sizeintnumber of windows to sample in each training batch, default uses all.1024
inference_windows_batch_sizeintnumber of windows to sample in each inference batch, -1 uses all.-1
start_padding_enabledboolif True, the model will pad the time series with zeros at the beginning, by input size.False
training_data_availability_thresholdUnion[float, List[float]]minimum fraction of valid data points required for training windows. Single float applies to both insample and outsample; list of two floats specifies [insample_fraction, outsample_fraction]. Default 0.0 allows windows with only 1 valid data point (current behavior).0.0
step_sizeintstep size between each window of temporal data.1
scaler_typestrtype of scaler for temporal inputs normalization see temporal scalers.‘identity’
random_seedintrandom_seed for pytorch initializer and numpy generators.1
drop_last_loaderboolif True TimeSeriesDataLoader drops last non-full batch.False
aliasstroptional, Custom name of the model.None
optimizerSubclass of ‘torch.optim.Optimizer’optional, user specified optimizer instead of the default choice (Adam).None
optimizer_kwargsdictoptional, list of parameters used by the user specified optimizer.None
lr_schedulerSubclass of ‘torch.optim.lr_scheduler.LRScheduler’optional, user specified lr_scheduler instead of the default choice (StepLR).None
lr_scheduler_kwargsdictoptional, list of parameters used by the user specified lr_scheduler.None
dataloader_kwargsdictoptional, list of parameters passed into the PyTorch Lightning dataloader by the TimeSeriesDataLoader.None
**trainer_kwargsintkeyword trainer arguments inherited from PyTorch Lighning’s trainer.

​
NHITS.fit

fit(
    dataset, val_size=0, test_size=0, random_seed=None, distributed_config=None
)
Fit. The fit method, optimizes the neural network’s weights using the initialization parameters (learning_rate, windows_batch_size, …) and the loss function as defined during the initialization. Within fit we use a PyTorch Lightning Trainer that inherits the initialization’s self.trainer_kwargs, to customize its inputs, see PL’s trainer arguments. The method is designed to be compatible with SKLearn-like classes and in particular to be compatible with the StatsForecast library. By default the model is not saving training checkpoints to protect disk memory, to get them change enable_checkpointing=True in __init__. Parameters:
NameTypeDescriptionDefault
datasetTimeSeriesDatasetNeuralForecast’s TimeSeriesDataset, see documentation.required
val_sizeintValidation size for temporal cross-validation.0
random_seedintRandom seed for pytorch initializer and numpy generators, overwrites model.init’s.None
test_sizeintTest size for temporal cross-validation.0
Returns:
TypeDescription
None

​
NHITS.predict

predict(
    dataset,
    test_size=None,
    step_size=1,
    random_seed=None,
    quantiles=None,
    h=None,
    explainer_config=None,
    **data_module_kwargs
)
Predict. Neural network prediction with PL’s Trainer execution of predict_step. Parameters:
NameTypeDescriptionDefault
datasetTimeSeriesDatasetNeuralForecast’s TimeSeriesDataset, see documentation.required
test_sizeintTest size for temporal cross-validation.None
step_sizeintStep size between each window.1
random_seedintRandom seed for pytorch initializer and numpy generators, overwrites model.init’s.None
quantileslistTarget quantiles to predict.None
hintPrediction horizon, if None, uses the model’s fitted horizon. Defaults to None.None
explainer_configdictconfiguration for explanations.None
**data_module_kwargsdictPL’s TimeSeriesDataModule args, see documentation.
Returns:
TypeDescription
None

​
Usage Example

import pandas as pd
import matplotlib.pyplot as plt

from neuralforecast import NeuralForecast
from neuralforecast.models import NHITS
from neuralforecast.losses.pytorch import DistributionLoss
from neuralforecast.utils import AirPassengersPanel, AirPassengersStatic

Y_train_df = AirPassengersPanel[AirPassengersPanel.ds<AirPassengersPanel['ds'].values[-12]].reset_index(drop=True) # 132 train
Y_test_df = AirPassengersPanel[AirPassengersPanel.ds>=AirPassengersPanel['ds'].values[-12]].reset_index(drop=True) # 12 test

model = NHITS(h=12,
              input_size=24,
              loss=DistributionLoss(distribution='StudentT', level=[80, 90], return_params=True),
              stat_exog_list=['airline1'],
              futr_exog_list=['trend'],
              n_freq_downsample=[2, 1, 1],
              scaler_type='robust',
              max_steps=200,
              early_stop_patience_steps=2,
              inference_windows_batch_size=1,
              val_check_steps=10,
              learning_rate=1e-3)

fcst = NeuralForecast(models=[model], freq='ME')
fcst.fit(df=Y_train_df, static_df=AirPassengersStatic, val_size=12)
forecasts = fcst.predict(futr_df=Y_test_df)

# Plot quantile predictions
Y_hat_df = forecasts.reset_index(drop=False).drop(columns=['unique_id','ds'])
plot_df = pd.concat([Y_test_df, Y_hat_df], axis=1)
plot_df = pd.concat([Y_train_df, plot_df])

plot_df = plot_df[plot_df.unique_id=='Airline1'].drop('unique_id', axis=1)
plt.plot(plot_df['ds'], plot_df['y'], c='black', label='True')
plt.plot(plot_df['ds'], plot_df['NHITS-median'], c='blue', label='median')
plt.fill_between(x=plot_df['ds'][-12:], 
                 y1=plot_df['NHITS-lo-90'][-12:].values, 
                 y2=plot_df['NHITS-hi-90'][-12:].values,
                 alpha=0.4, label='level 90')
plt.legend()
plt.grid()
plt.plot()