source

​
MLP

 MLP (h, input_size, futr_exog_list=None, hist_exog_list=None,
      stat_exog_list=None, exclude_insample_y=False, num_layers=2,
      hidden_size=1024, loss=MAE(), valid_loss=None, max_steps:int=1000,
      learning_rate:float=0.001, num_lr_decays:int=-1,
      early_stop_patience_steps:int=-1, val_check_steps:int=100,
      batch_size:int=32, valid_batch_size:Optional[int]=None,
      windows_batch_size=1024, inference_windows_batch_size=-1,
      start_padding_enabled=False, step_size:int=1,
      scaler_type:str='identity', random_seed:int=1,
      num_workers_loader:int=0, drop_last_loader:bool=False,
      optimizer=None, optimizer_kwargs=None, lr_scheduler=None,
      lr_scheduler_kwargs=None, dataloader_kwargs=None, **trainer_kwargs)

*MLP

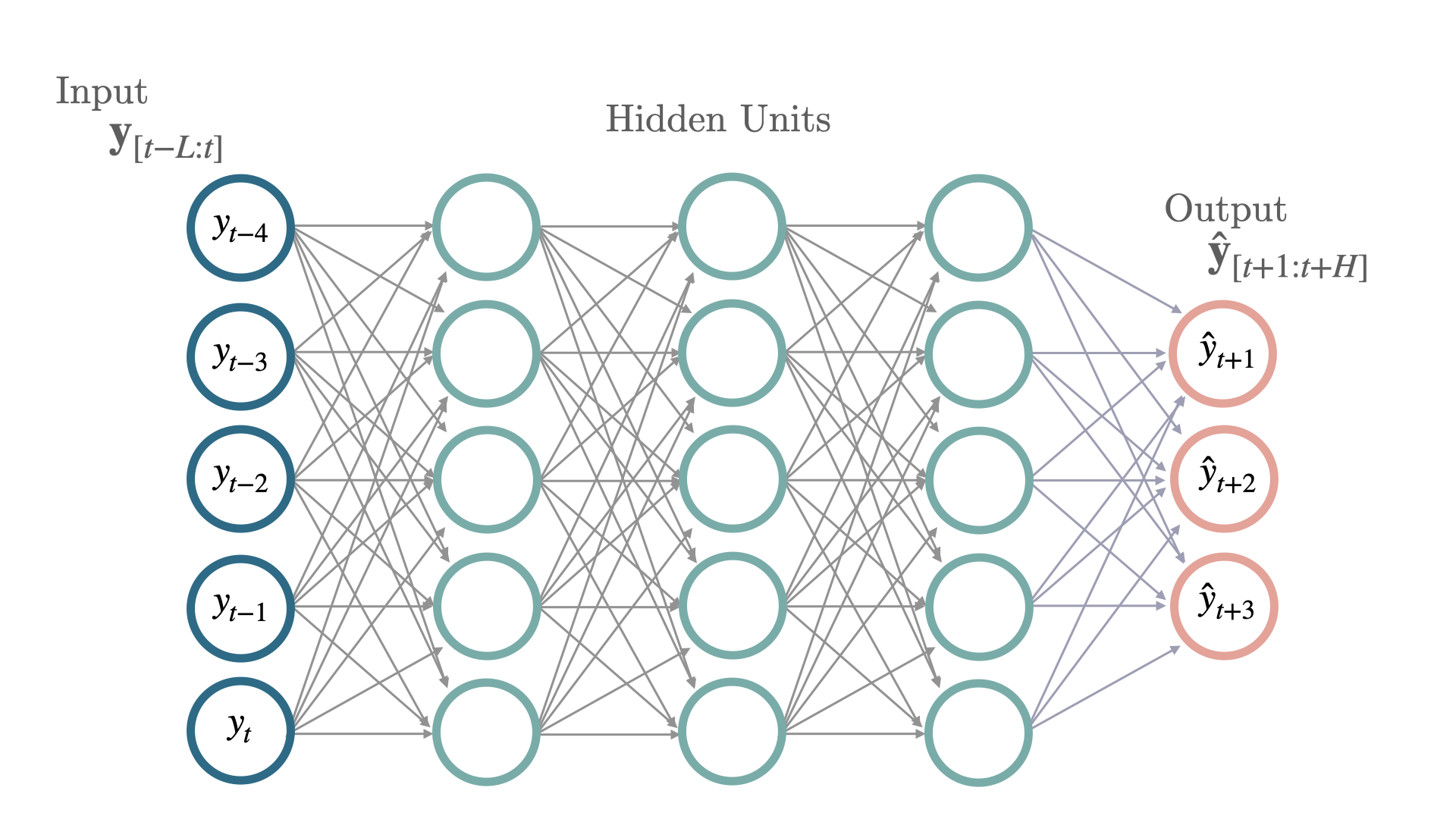
Simple Multi Layer Perceptron architecture (MLP). This deep neural network has constant units through its layers, each with ReLU non-linearities, it is trained using ADAM stochastic gradient descent. The network accepts static, historic and future exogenous data, flattens the inputs and learns fully connected relationships against the target variable.

Parameters:
h: int, forecast horizon.
input_size: int, considered autorregresive inputs (lags), y=[1,2,3,4] input_size=2 -> lags=[1,2].
stat_exog_list: str list, static exogenous columns.
hist_exog_list: str list, historic exogenous columns.
futr_exog_list: str list, future exogenous columns.
exclude_insample_y: bool=False, the model skips the autoregressive features y[t-input_size:t] if True.
n_layers: int, number of layers for the MLP.
hidden_size: int, number of units for each layer of the MLP.
loss: PyTorch module, instantiated train loss class from losses collection.
valid_loss: PyTorch module=loss, instantiated valid loss class from losses collection.
max_steps: int=1000, maximum number of training steps.
learning_rate: float=1e-3, Learning rate between (0, 1).
num_lr_decays: int=-1, Number of learning rate decays, evenly distributed across max_steps.
early_stop_patience_steps: int=-1, Number of validation iterations before early stopping.
val_check_steps: int=100, Number of training steps between every validation loss check.
batch_size: int=32, number of different series in each batch.
valid_batch_size: int=None, number of different series in each validation and test batch, if None uses batch_size.
windows_batch_size: int=1024, number of windows to sample in each training batch, default uses all.
inference_windows_batch_size: int=-1, number of windows to sample in each inference batch, -1 uses all.
start_padding_enabled: bool=False, if True, the model will pad the time series with zeros at the beginning, by input size.
step_size: int=1, step size between each window of temporal data.
scaler_type: str=‘identity’, type of scaler for temporal inputs normalization see temporal scalers.
random_seed: int=1, random_seed for pytorch initializer and numpy generators.
num_workers_loader: int=os.cpu_count(), workers to be used by TimeSeriesDataLoader.
drop_last_loader: bool=False, if True TimeSeriesDataLoader drops last non-full batch.
alias: str, optional, Custom name of the model.
optimizer: Subclass of ‘torch.optim.Optimizer’, optional, user specified optimizer instead of the default choice (Adam).
optimizer_kwargs: dict, optional, list of parameters used by the user specified optimizer.
lr_scheduler: Subclass of ‘torch.optim.lr_scheduler.LRScheduler’, optional, user specified lr_scheduler instead of the default choice (StepLR).
lr_scheduler_kwargs: dict, optional, list of parameters used by the user specified lr_scheduler.

dataloader_kwargs: dict, optional, list of parameters passed into the PyTorch Lightning dataloader by the TimeSeriesDataLoader.
**trainer_kwargs: int, keyword trainer arguments inherited from PyTorch Lighning’s trainer.
*

​
MLP.fit

 MLP.fit (dataset, val_size=0, test_size=0, random_seed=None,
          distributed_config=None)

*Fit.

The fit method, optimizes the neural network’s weights using the initialization parameters (learning_rate, windows_batch_size, …) and the loss function as defined during the initialization. Within fit we use a PyTorch Lightning Trainer that inherits the initialization’s self.trainer_kwargs, to customize its inputs, see PL’s trainer arguments.

The method is designed to be compatible with SKLearn-like classes and in particular to be compatible with the StatsForecast library.

By default the model is not saving training checkpoints to protect disk memory, to get them change enable_checkpointing=True in __init__.

Parameters:
dataset: NeuralForecast’s TimeSeriesDataset, see documentation.
val_size: int, validation size for temporal cross-validation.
random_seed: int=None, random_seed for pytorch initializer and numpy generators, overwrites model.__init__’s.
test_size: int, test size for temporal cross-validation.
*

​
MLP.predict

 MLP.predict (dataset, test_size=None, step_size=1, random_seed=None,
              **data_module_kwargs)

*Predict.

Neural network prediction with PL’s Trainer execution of predict_step.

Parameters:
dataset: NeuralForecast’s TimeSeriesDataset, see documentation.
test_size: int=None, test size for temporal cross-validation.
step_size: int=1, Step size between each window.
random_seed: int=None, random_seed for pytorch initializer and numpy generators, overwrites model.__init__’s.
**data_module_kwargs: PL’s TimeSeriesDataModule args, see documentation.*

​
Usage Example

import pandas as pd
import matplotlib.pyplot as plt

from neuralforecast import NeuralForecast
from neuralforecast.models import MLP
from neuralforecast.losses.pytorch import DistributionLoss
from neuralforecast.utils import AirPassengersPanel, AirPassengersStatic

Y_train_df = AirPassengersPanel[AirPassengersPanel.ds<AirPassengersPanel['ds'].values[-12]] # 132 train
Y_test_df = AirPassengersPanel[AirPassengersPanel.ds>=AirPassengersPanel['ds'].values[-12]].reset_index(drop=True) # 12 test

model = MLP(h=12, input_size=24,
            loss=DistributionLoss(distribution='Normal', level=[80, 90]),
            scaler_type='robust',
            learning_rate=1e-3,
            max_steps=200,
            val_check_steps=10,
            early_stop_patience_steps=2)

fcst = NeuralForecast(
    models=[model],
    freq='M'
)
fcst.fit(df=Y_train_df, static_df=AirPassengersStatic, val_size=12)
forecasts = fcst.predict(futr_df=Y_test_df)

Y_hat_df = forecasts.reset_index(drop=False).drop(columns=['unique_id','ds'])
plot_df = pd.concat([Y_test_df, Y_hat_df], axis=1)
plot_df = pd.concat([Y_train_df, plot_df])

plot_df = plot_df[plot_df.unique_id=='Airline1'].drop('unique_id', axis=1)
plt.plot(plot_df['ds'], plot_df['y'], c='black', label='True')
plt.plot(plot_df['ds'], plot_df['MLP-median'], c='blue', label='median')
plt.fill_between(x=plot_df['ds'][-12:], 
                 y1=plot_df['MLP-lo-90'][-12:].values, 
                 y2=plot_df['MLP-hi-90'][-12:].values,
                 alpha=0.4, label='level 90')
plt.grid()
plt.legend()
plt.plot()
LSTMMLPMultivariate