In this example, we’ll forecast the volatility of the S&P 500 and several publicly traded companies using GARCH and ARCH models
Prerequisites This tutorial assumes basic familiarity with StatsForecast. For a minimal example visit the Quick Start
Introduction
The Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model is used for time series that exhibit non-constant volatility over time. Here volatility refers to the conditional standard deviation. The GARCH(p,q) model is given by where is independent and identically distributed with zero mean and unit variance, and evolves according to The coefficients in the equation above must satisfy the following conditions:- , for all , and for all
- . Here it is assumed that for and for .
- Install libraries
- Load and explore the data
- Train models
- Perform time series cross-validation
- Evaluate results
- Forecast volatility
Tip You can use Colab to run this Notebook interactively
Install libraries
We assume that you have StatsForecast already installed. If not, check this guide for instructions on how to install StatsForecast Install the necessary packages usingpip install statsforecast
Load and explore the data
In this tutorial, we’ll use the last 5 years of prices from the S&P 500 and several publicly traded companies. The data can be downloaded from Yahoo! Finance using yfinance. To install it, usepip install yfinance.
pandas to deal with the dataframes.
| Price | Adj Close | … | Volume | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ticker | AAPL | AMZN | GOOG | META | MSFT | NFLX | NKE | NVDA | SPY | TSLA | … | AAPL | AMZN | GOOG | META | MSFT | NFLX | NKE | NVDA | SPY | TSLA |
| Date | |||||||||||||||||||||
| 2018-01-01 | 39.388084 | 72.544502 | 58.353695 | 186.328979 | 88.027702 | 270.299988 | 63.341862 | 6.078998 | 252.565216 | 23.620667 | … | 2638717600 | 1927424000 | 574768000 | 495655700 | 574258400 | 238377600 | 157812200 | 11456216000 | 1985506700 | 1864072500 |
| 2018-02-01 | 41.902908 | 75.622498 | 55.101181 | 177.784729 | 86.878807 | 291.380005 | 62.236938 | 5.985018 | 243.381882 | 22.870667 | … | 3711577200 | 2755680000 | 847640000 | 516251600 | 725663300 | 184585800 | 160317000 | 14915528000 | 2923722000 | 1637850000 |
| 2018-03-01 | 39.631344 | 72.366997 | 51.463116 | 159.310333 | 84.959763 | 295.350006 | 61.689133 | 5.731123 | 235.766373 | 17.742001 | … | 2854910800 | 2608002000 | 907066000 | 996201700 | 750754800 | 263449400 | 174066700 | 14118440000 | 2323561800 | 2359027500 |
| 2018-04-01 | 39.036106 | 78.306503 | 50.741886 | 171.483688 | 87.054207 | 312.459991 | 63.691761 | 5.565567 | 237.934006 | 19.593332 | … | 2664617200 | 2598392000 | 834318000 | 750072700 | 668130700 | 262006000 | 158981900 | 11144008000 | 1998466500 | 2854662000 |
| 2018-05-01 | 44.140598 | 81.481003 | 54.116600 | 191.204315 | 92.006393 | 351.600006 | 66.867508 | 6.240908 | 243.717957 | 18.982000 | … | 2483905200 | 1432310000 | 636988000 | 401144100 | 509417900 | 142050800 | 129566300 | 11978240000 | 1606397200 | 2333671500 |
yfinance returns has a
MultiIndex,
so we need to select both the adjusted price and the tickers.
| Ticker | Date | SPY | MSFT | AAPL | GOOG | AMZN | TSLA | NVDA | META | NKE | NFLX |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2018-01-01 | 252.565216 | 88.027702 | 39.388084 | 58.353695 | 72.544502 | 23.620667 | 6.078998 | 186.328979 | 63.341862 | 270.299988 |
| 1 | 2018-02-01 | 243.381882 | 86.878807 | 41.902908 | 55.101181 | 75.622498 | 22.870667 | 5.985018 | 177.784729 | 62.236938 | 291.380005 |
| 2 | 2018-03-01 | 235.766373 | 84.959763 | 39.631344 | 51.463116 | 72.366997 | 17.742001 | 5.731123 | 159.310333 | 61.689133 | 295.350006 |
| 3 | 2018-04-01 | 237.934006 | 87.054207 | 39.036106 | 50.741886 | 78.306503 | 19.593332 | 5.565567 | 171.483688 | 63.691761 | 312.459991 |
| 4 | 2018-05-01 | 243.717957 | 92.006393 | 44.140598 | 54.116600 | 81.481003 | 18.982000 | 6.240908 | 191.204315 | 66.867508 | 351.600006 |
unique_id, ds and y:
unique_id: (string, int or category) A unique identifier for the series.ds: (datestamp or int) A datestamp in format YYYY-MM-DD or YYYY-MM-DD HH:MM:SS or an integer indexing time.y: (numeric) The measurement we wish to forecast.
price.
| unique_id | ds | y | |
|---|---|---|---|
| 0 | SPY | 2018-01-01 | 252.565216 |
| 1 | SPY | 2018-02-01 | 243.381882 |
| 2 | SPY | 2018-03-01 | 235.766373 |
| 3 | SPY | 2018-04-01 | 237.934006 |
| 4 | SPY | 2018-05-01 | 243.717957 |
| … | … | … | … |
| 595 | NFLX | 2022-08-01 | 223.559998 |
| 596 | NFLX | 2022-09-01 | 235.440002 |
| 597 | NFLX | 2022-10-01 | 291.880005 |
| 598 | NFLX | 2022-11-01 | 305.529999 |
| 599 | NFLX | 2022-12-01 | 294.880005 |
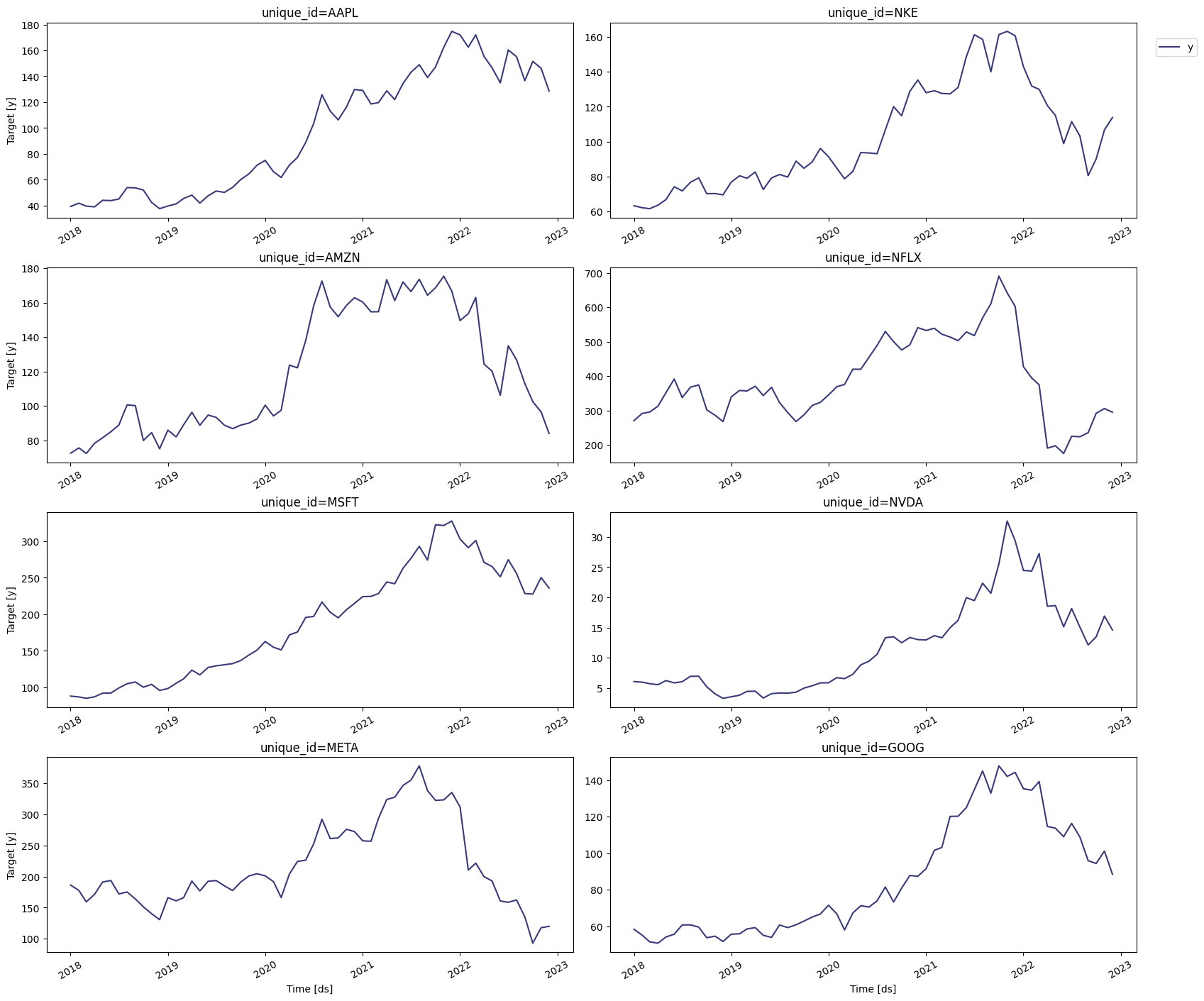
plot method of the StatsForecast
class.
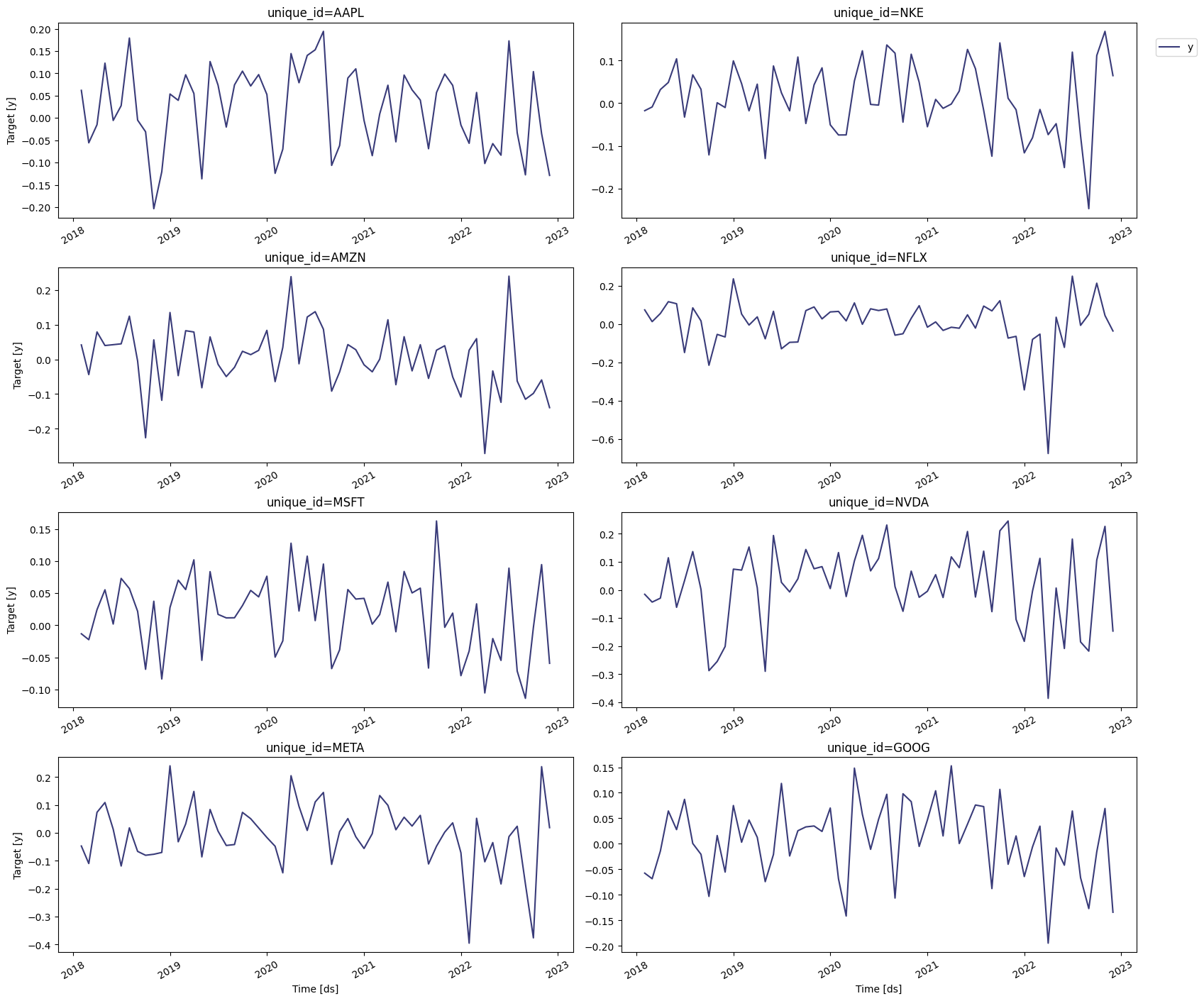
numpy.
| unique_id | ds | y | |
|---|---|---|---|
| 0 | SPY | 2018-01-01 | NaN |
| 1 | SPY | 2018-02-01 | -0.037038 |
| 2 | SPY | 2018-03-01 | -0.031790 |
| 3 | SPY | 2018-04-01 | 0.009152 |
| 4 | SPY | 2018-05-01 | 0.024018 |
| … | … | … | … |
| 595 | NFLX | 2022-08-01 | -0.005976 |
| 596 | NFLX | 2022-09-01 | 0.051776 |
| 597 | NFLX | 2022-10-01 | 0.214887 |
| 598 | NFLX | 2022-11-01 | 0.045705 |
| 599 | NFLX | 2022-12-01 | -0.035479 |
Warning
If the order of the data is very small (say ),
scipy.optimize.minimize might not terminate successfully. In this
case, rescale the data and then generate the GARCH or ARCH model.
Train models
We first need to import the GARCH and the ARCH models fromstatsforecast.models, and then we
need to fit them by instantiating a new StatsForecast object. Notice
that we’ll be using different values of and . In the next
section, we’ll determine which ones produce the most accurate model
using cross-validation. We’ll also import the
Naive model since we’ll use it as a
baseline.
df: The dataframe with the training data.models: The list of models defined in the previous step.freq: A string indicating the frequency of the data. Here we’ll use MS, which correspond to the start of the month. You can see the list of panda’s available frequencies here.n_jobs: An integer that indicates the number of jobs used in parallel processing. Use -1 to select all cores.
Perform time series cross-validation
Time series cross-validation is a method for evaluating how a model would have performed in the past. It works by defining a sliding window across the historical data and predicting the period following it. Here we’ll use StatsForecast’scross-validation method to determine the
most accurate model for the S&P 500 and the companies selected.
This method takes the following arguments:
df: The dataframe with the training data.h(int): represents the h steps into the future that will be forecasted.step_size(int): step size between each window, meaning how often do you want to run the forecasting process.n_windows(int): number of windows used for cross-validation, meaning the number of forecasting processes in the past you want to evaluate.
cv_df object is a dataframe with the following columns:
unique_id: series identifier.ds: datestamp or temporal indexcutoff: the last datestamp or temporal index for then_windows.y: true value"model": columns with the model’s name and fitted value.
| unique_id | ds | cutoff | actual | ARCH(1) | ARCH(2) | GARCH(1,1) | GARCH(1,2) | GARCH(2,2) | GARCH(2,1) | Naive | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | AAPL | 2022-01-01 | 2021-12-01 | -0.015837 | 0.142421 | 0.144016 | 0.142954 | 0.141682 | 0.141682 | 0.144015 | 0.073061 |
| 1 | AAPL | 2022-02-01 | 2021-12-01 | -0.056856 | -0.056893 | -0.057158 | -0.056388 | -0.058786 | -0.058785 | -0.057158 | 0.073061 |
| 2 | AAPL | 2022-03-01 | 2021-12-01 | 0.057156 | -0.045901 | -0.046479 | -0.047513 | -0.045711 | -0.045711 | -0.046478 | 0.073061 |
| 3 | AAPL | 2022-04-01 | 2022-03-01 | -0.102178 | 0.138650 | 0.140222 | 0.228138 | 0.136118 | 0.136132 | 0.140211 | 0.057156 |
| 4 | AAPL | 2022-05-01 | 2022-03-01 | -0.057505 | -0.056007 | -0.056268 | -0.087833 | -0.057078 | -0.057085 | -0.056265 | 0.057156 |
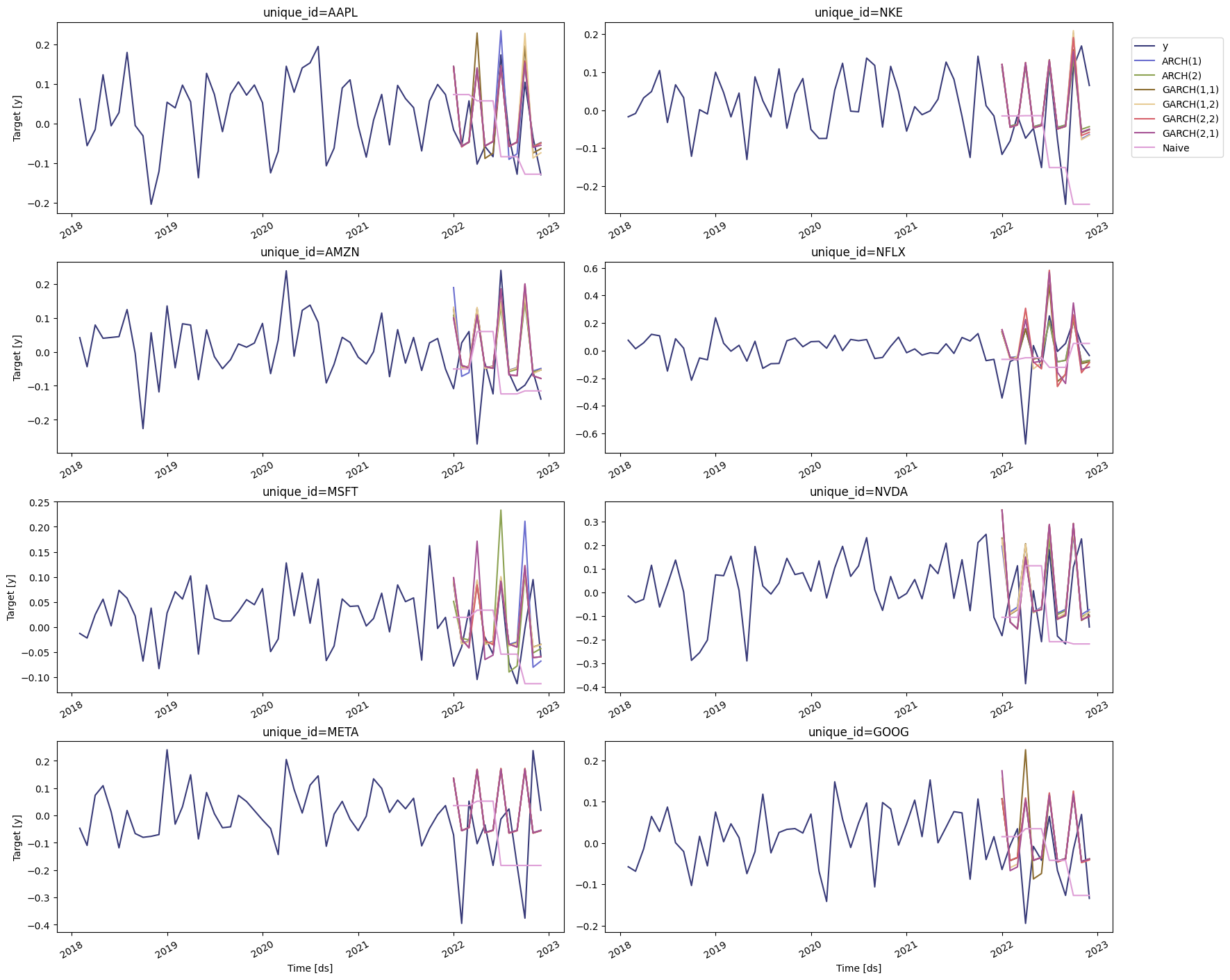
Evaluate results
To compute the accuracy of the forecasts, we’ll use the mean average error (mae), which is the sum of the absolute errors divided by the number of forecasts.| ARCH(1) | ARCH(2) | GARCH(1,1) | GARCH(1,2) | GARCH(2,2) | GARCH(2,1) | Naive | |
|---|---|---|---|---|---|---|---|
| unique_id | |||||||
| AAPL | 0.071773 | 0.068927 | 0.080182 | 0.075321 | 0.069187 | 0.068817 | 0.110426 |
| AMZN | 0.127390 | 0.113613 | 0.118859 | 0.119930 | 0.109910 | 0.109910 | 0.115189 |
| GOOG | 0.093849 | 0.093753 | 0.109662 | 0.101583 | 0.094648 | 0.103389 | 0.083233 |
| META | 0.198334 | 0.198893 | 0.199615 | 0.199711 | 0.199712 | 0.198892 | 0.185346 |
| MSFT | 0.082373 | 0.075055 | 0.072241 | 0.072765 | 0.073006 | 0.082066 | 0.086951 |
| NFLX | 0.159386 | 0.159528 | 0.199623 | 0.232477 | 0.230075 | 0.230770 | 0.167421 |
| NKE | 0.108337 | 0.098918 | 0.103366 | 0.110278 | 0.107179 | 0.102708 | 0.160404 |
| NVDA | 0.189461 | 0.207871 | 0.198999 | 0.196170 | 0.211932 | 0.211940 | 0.215289 |
| SPY | 0.058511 | 0.058583 | 0.058701 | 0.062492 | 0.057053 | 0.068192 | 0.089012 |
| TSLA | 0.192003 | 0.192618 | 0.190225 | 0.192354 | 0.191620 | 0.191423 | 0.218857 |
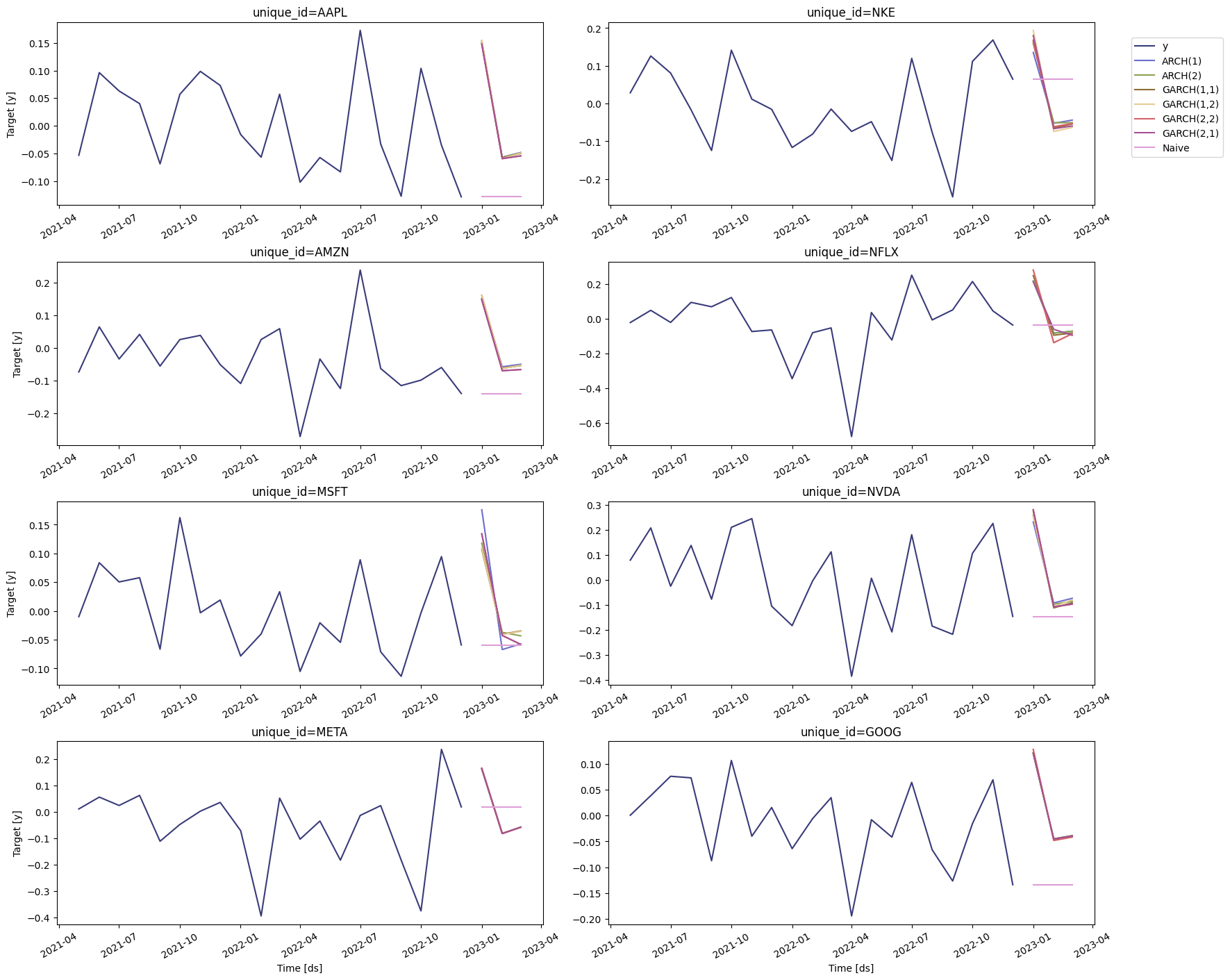
Forecast volatility
We can now generate a forecast for the next quarter. To do this, we’ll use theforecast method, which requires the following arguments:
h: (int) The forecasting horizon.level: (list[float]) The confidence levels of the prediction intervalsfitted: (bool = False) Returns insample predictions.
| unique_id | ds | ARCH(1) | ARCH(1)-lo-95 | ARCH(1)-lo-80 | ARCH(1)-hi-80 | ARCH(1)-hi-95 | ARCH(2) | ARCH(2)-lo-95 | ARCH(2)-lo-80 | … | GARCH(2,1) | GARCH(2,1)-lo-95 | GARCH(2,1)-lo-80 | GARCH(2,1)-hi-80 | GARCH(2,1)-hi-95 | Naive | Naive-lo-80 | Naive-lo-95 | Naive-hi-80 | Naive-hi-95 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | AAPL | 2023-01-01 | 0.150457 | 0.133641 | 0.139462 | 0.161453 | 0.167273 | 0.150158 | 0.133409 | 0.139206 | … | 0.147602 | 0.131418 | 0.137020 | 0.158184 | 0.163786 | -0.128762 | -0.284462 | -0.366885 | 0.026939 | 0.109362 |
| 1 | AAPL | 2023-02-01 | -0.056943 | -0.073924 | -0.068046 | -0.045839 | -0.039961 | -0.057207 | -0.074346 | -0.068414 | … | -0.059512 | -0.078060 | -0.071640 | -0.047384 | -0.040964 | -0.128762 | -0.348956 | -0.465520 | 0.091433 | 0.207997 |
| 2 | AAPL | 2023-03-01 | -0.048391 | -0.064843 | -0.059148 | -0.037633 | -0.031939 | -0.049282 | -0.066345 | -0.060439 | … | -0.054539 | -0.075438 | -0.068204 | -0.040875 | -0.033641 | -0.128762 | -0.398443 | -0.541204 | 0.140920 | 0.283681 |
| 3 | AMZN | 2023-01-01 | 0.152147 | 0.134952 | 0.140904 | 0.163391 | 0.169343 | 0.148658 | 0.132242 | 0.137924 | … | 0.148599 | 0.132196 | 0.137873 | 0.159324 | 0.165001 | -0.139141 | -0.315716 | -0.409190 | 0.037435 | 0.130909 |
| 4 | AMZN | 2023-02-01 | -0.057301 | -0.074497 | -0.068545 | -0.046058 | -0.040106 | -0.061187 | -0.080794 | -0.074007 | … | -0.069303 | -0.094457 | -0.085750 | -0.052856 | -0.044150 | -0.139141 | -0.388856 | -0.521048 | 0.110575 | 0.242767 |
plot
method:
level: (list[int]) The confidence levels for the prediction intervals (this was already defined).unique_ids: (list[str, int or category]) The ids to plot.models: (list(str)). The model to plot. In this case, is the model selected by cross-validation.
References
- Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica: Journal of the econometric society, 987-1007.
- Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of econometrics, 31(3), 307-327.
- Hamilton, J. D. (1994). Time series analysis. Princeton university press.
- Tsay, R. S. (2005). Analysis of financial time series. John wiley & sons.

