Learn how to generate calibrated prediction intervals for any forecasting model using conformal prediction, a distribution-free method for uncertainty quantification in Python.
What You’ll Learn
In this tutorial, you’ll discover how to:- Generate calibrated prediction intervals without distributional assumptions
- Apply conformal prediction to any forecasting model in Python
- Implement uncertainty quantification with StatsForecast’s
ConformalIntervals - Compare conformal prediction with traditional uncertainty methods
- Evaluate prediction interval coverage and calibration
Prerequisites
This tutorial assumes basic familiarity with StatsForecast. For a minimal example visit the Quick StartWhat is Conformal Prediction?
Conformal prediction is a distribution-free framework for generating prediction intervals with guaranteed coverage properties. Unlike traditional methods that assume normally distributed errors, conformal prediction works with any forecasting model and provides well-calibrated uncertainty estimates without making distributional assumptions.Why Use Conformal Prediction for Time Series?
When generating forecasts, a point forecast alone doesn’t convey uncertainty. Prediction intervals quantify this uncertainty by providing a range of values where future observations are likely to fall. A properly calibrated 95% prediction interval should contain the actual value 95% of the time. The challenge: many forecasting models either don’t provide prediction intervals, or generate intervals that are poorly calibrated. Traditional statistical methods also assume normality, which often doesn’t hold in practice. Conformal prediction solves this by:- Working with any forecasting model (model-agnostic)
- Requiring no distributional assumptions
- Using cross-validation to generate calibrated intervals
- Providing theoretical coverage guarantees
- Treating the forecasting model as a black box
Conformal Prediction vs. Traditional Methods
| Method | Distributional Assumption | Model-Agnostic | Calibration Guarantee |
|---|---|---|---|
| Conformal Prediction | None | ✓ | ✓ |
| Bootstrap | Parametric assumptions | ✓ | ~ |
| Quantile Regression | None | ✓ | ~ |
| Statistical Models (ARIMA, ETS) | Normal errors | ✗ | ~ |
Models with Native Prediction Intervals
For models that already provide forecast distributions (like AutoARIMA, AutoETS), check Prediction Intervals. Conformal prediction is particularly useful for models that only produce point forecasts, or when you want distribution-free intervals.How Conformal Prediction Works
Conformal prediction uses cross-validation to generate prediction intervals:- Split the training data into multiple windows
- Train the model on each window and forecast the next period
- Calculate residuals (prediction errors) on the held-out data
- Construct intervals using the distribution of these residuals
Real-World Applications
Conformal prediction is particularly valuable for:- Demand forecasting: Inventory planning with quantified uncertainty
- Energy prediction: Load forecasting with reliable confidence bounds
- Financial forecasting: Risk management with calibrated intervals
- Production models: Any black-box forecasting model requiring uncertainty quantification
Install libraries
We assume that you have StatsForecast already installed. If not, check this guide for instructions on how to install StatsForecast Install the necessary packages usingpip install statsforecast
Load and explore the data
For this example, we’ll use the hourly dataset from the M4 Competition. We first need to download the data from a URL and then load it as apandas dataframe. Notice that we’ll load the train and the test data
separately. We’ll also rename the y column of the test data as
y_test.
| unique_id | ds | y | |
|---|---|---|---|
| 0 | H1 | 1 | 605.0 |
| 1 | H1 | 2 | 586.0 |
| 2 | H1 | 3 | 586.0 |
| 3 | H1 | 4 | 559.0 |
| 4 | H1 | 5 | 511.0 |
plot_series function from the
utilsforecast library. This function method has multiple parameters, and
the required ones to generate the plots in this notebook are explained
below.
df: Apandasdataframe with columns [unique_id,ds,y].forecasts_df: Apandasdataframe with columns [unique_id,ds] and models.plot_random: bool =True. Plots the time series randomly.models: List[str]. A list with the models we want to plot.level: List[float]. A list with the prediction intervals we want to plot.engine: str =matplotlib. It can also beplotly.plotlygenerates interactive plots, whilematplotlibgenerates static plots.
Implementing Conformal Prediction in Python
StatsForecast makes it simple to add conformal prediction to any forecasting model. We’ll demonstrate with models that don’t natively provide prediction intervals:- SeasonalExponentialSmoothing: A simple smoothing model
- ADIDA: Aggregation method for intermittent demand
- ARIMA: Traditional statistical model (to show distribution-free intervals)
Setting Up Conformal Intervals
The key is theConformalIntervals class, which requires two
parameters:
h: Forecast horizon (how many steps ahead to predict)n_windows: Number of cross-validation windows for calibration
Parameter Requirements
n_windows * hmust be less than your time series lengthn_windowsshould be at least 2 for reliable calibration- Larger
n_windowsimproves calibration but increases computation time
df: The dataframe with the training data.models: The list of models defined in the previous step.freq: A string indicating the frequency of the data. See pandas’ available frequencies.n_jobs: An integer that indicates the number of jobs used in parallel processing. Use -1 to select all cores.
Generating Forecasts with Prediction Intervals
Theforecast method generates both point forecasts and conformal
prediction intervals:
h: Forecast horizon (number of steps ahead)level: List of confidence levels (e.g.,[80, 90]for 80% and 90% intervals)
model-lo-{level}, model-hi-{level}).
| unique_id | ds | SeasonalES | SeasonalES-lo-90 | SeasonalES-lo-80 | SeasonalES-hi-80 | SeasonalES-hi-90 | ADIDA | ADIDA-lo-90 | ADIDA-lo-80 | ADIDA-hi-80 | ADIDA-hi-90 | ARIMA | ARIMA-lo-90 | ARIMA-lo-80 | ARIMA-hi-80 | ARIMA-hi-90 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | H1 | 701 | 624.132703 | 553.097423 | 556.359139 | 691.906266 | 695.167983 | 747.292568 | 599.519220 | 600.030467 | 894.554670 | 895.065916 | 618.078274 | 609.440076 | 610.583304 | 625.573243 | 626.716472 |
| 1 | H1 | 702 | 555.698193 | 496.653559 | 506.833156 | 604.563231 | 614.742827 | 747.292568 | 491.669220 | 498.330467 | 996.254670 | 1002.915916 | 549.789291 | 510.464070 | 515.232352 | 584.346231 | 589.114513 |
| 2 | H1 | 703 | 514.403029 | 462.673117 | 464.939840 | 563.866218 | 566.132941 | 747.292568 | 475.105038 | 475.793791 | 1018.791346 | 1019.480099 | 508.099925 | 496.574844 | 496.990264 | 519.209587 | 519.625007 |
| 3 | H1 | 704 | 482.057899 | 433.030711 | 436.161413 | 527.954385 | 531.085087 | 747.292568 | 440.069220 | 440.130467 | 1054.454670 | 1054.515916 | 486.376622 | 471.141813 | 471.516997 | 501.236246 | 501.611431 |
| 4 | H1 | 705 | 460.222522 | 414.270186 | 416.959492 | 503.485552 | 506.174858 | 747.292568 | 415.805038 | 416.193791 | 1078.391346 | 1078.780099 | 470.159478 | 445.162316 | 446.808608 | 493.510348 | 495.156640 |
Visualizing Calibrated Prediction Intervals
Let’s examine the prediction intervals for each model to understand their characteristics and calibration quality.SeasonalExponentialSmoothing: Well-Calibrated Intervals
The conformal prediction intervals show proper nesting: the 80% interval is contained within the 90% interval, indicating well-calibrated uncertainty quantification. Even though this model only produces point forecasts, conformal prediction successfully generates meaningful prediction intervals.
ADIDA: Wider Intervals for Weaker Models
Models with higher prediction errors produce wider conformal intervals. This is a feature, not a bug: the interval width honestly reflects the model’s uncertainty. A better-fitting model will produce narrower, more informative intervals.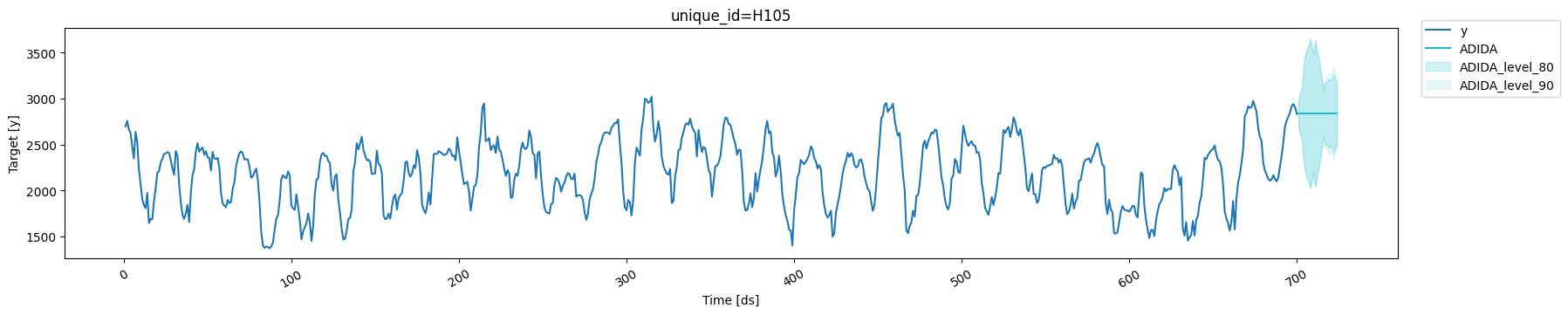
ARIMA: Distribution-Free Alternative
ARIMA models typically provide prediction intervals assuming normally distributed errors. By using conformal prediction, we get distribution-free intervals that don’t rely on this assumption, which is valuable when the normality assumption is questionable.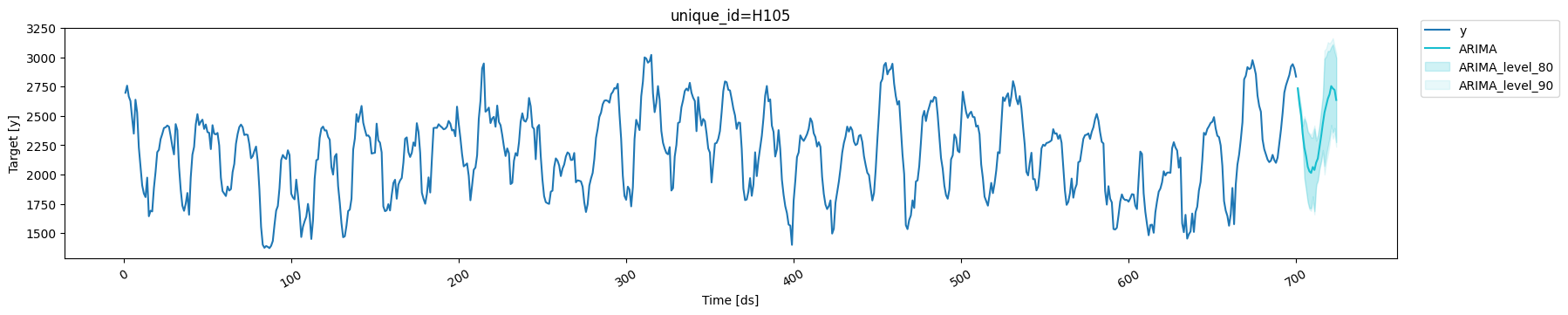
Alternative: Setting Conformal Intervals on StatsForecast Object
You can apply conformal prediction to all models at once by specifyingprediction_intervals in the StatsForecast object. This is convenient
when you want the same conformal setup for multiple models.
| unique_id | ds | SES | SES-lo-80 | SES-hi-80 | ADIDA | ADIDA-lo-80 | ADIDA-hi-80 | |
|---|---|---|---|---|---|---|---|---|
| 0 | H1 | 701 | 742.669064 | 649.221405 | 836.116722 | 747.292568 | 600.030467 | 894.554670 |
| 1 | H1 | 702 | 742.669064 | 550.551324 | 934.786804 | 747.292568 | 498.330467 | 996.254670 |
| 2 | H1 | 703 | 742.669064 | 523.621405 | 961.716722 | 747.292568 | 475.793791 | 1018.791346 |
| 3 | H1 | 704 | 742.669064 | 488.121405 | 997.216722 | 747.292568 | 440.130467 | 1054.454670 |
| 4 | H1 | 705 | 742.669064 | 464.021405 | 1021.316722 | 747.292568 | 416.193791 | 1078.391346 |
Future work
Conformal prediction has become a powerful framework for uncertainty quantification, providing well-calibrated prediction intervals without making any distributional assumptions. Its use has surged in both academia and industry over the past few years. We’ll continue working on it, and future tutorials may include:- Exploring larger datasets
- Incorporating industry-specific examples
- Investigating specialized methods like the jackknife+ that are closely related to conformal prediction (for details on the jackknife+ see here)
Key Takeaways
Summary: Conformal Prediction for Time Series
- Model-agnostic: Works with any forecasting model in Python
- Distribution-free: No normality assumptions required
- Well-calibrated: Theoretical coverage guarantees
- Easy to implement: Just add
ConformalIntervalsto your StatsForecast models - Flexible: Apply to individual models or all models at once
- Try conformal prediction on your own forecasting problems
- Experiment with different
n_windowsvalues for optimal calibration - Compare with native prediction intervals from statistical models
- Explore advanced uncertainty quantification methods

