Probabilistic Forecasting

Prerequisites

This tutorial assumes basic familiarity with StatsForecast. For a minimal example visit the Quick Start

​

Introduction

When we generate a forecast, we usually produce a single value known as the point forecast. This value, however, doesn’t tell us anything about the uncertainty associated with the forecast. To have a measure of this uncertainty, we need prediction intervals.

A prediction interval is a range of values that the forecast can take with a given probability. Hence, a 95% prediction interval should contain a range of values that include the actual future value with probability 95%. Probabilistic forecasting aims to generate the full forecast distribution. Point forecasting, on the other hand, usually returns the mean or the median or said distribution. However, in real-world scenarios, it is better to forecast not only the most probable future outcome, but many alternative outcomes as well.

StatsForecast has many models that can generate point forecasts. It also has probabilistic models than generate the same point forecasts and their prediction intervals. These models are stochastic data generating processes that can produce entire forecast distributions. By the end of this tutorial, you’ll have a good understanding of the probabilistic models available in StatsForecast and will be able to use them to generate point forecasts and prediction intervals. Furthermore, you’ll also learn how to generate plots with the historical data, the point forecasts, and the prediction intervals.

Important

Although the terms are often confused, prediction intervals are not the same as confidence intervals.

Warning

In practice, most prediction intervals are too narrow since models do not account for all sources of uncertainty. A discussion about this can be found here.

Outline:

1. Install libraries
2. Load and explore the data
3. Train models
4. Plot prediction intervals

Tip

You can use Colab to run this Notebook interactively

​

Install libraries

We assume that you have StatsForecast already installed. If not, check this guide for instructions on how to install StatsForecast

Install the necessary packages using pip install statsforecast

​

Load and explore the data

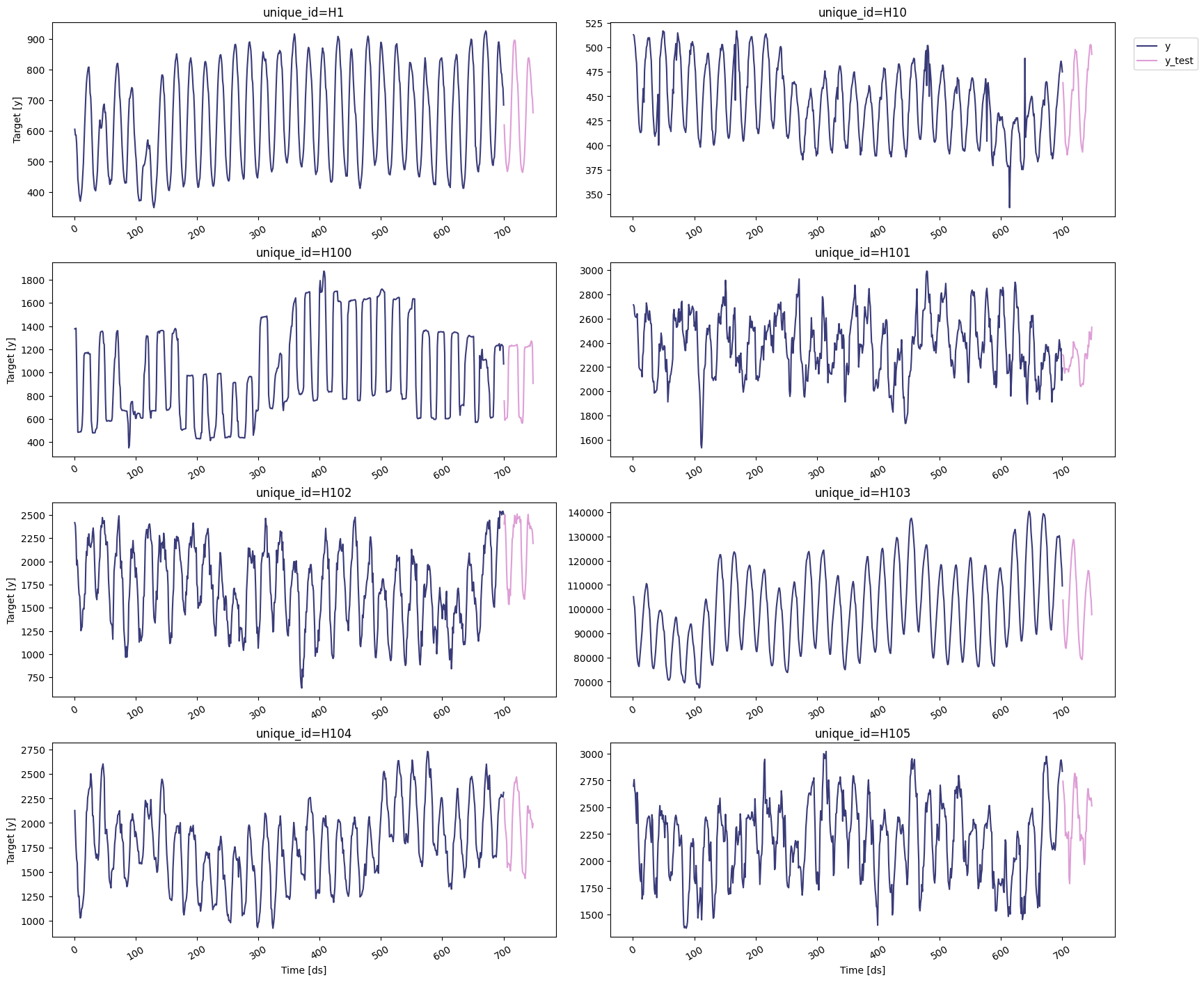
For this example, we’ll use the hourly dataset from the M4 Competition. We first need to download the data from a URL and then load it as a pandas dataframe. Notice that we’ll load the train and the test data separately. We’ll also rename the y column of the test data as y_test.

import pandas as pd

train = pd.read_csv('https://auto-arima-results.s3.amazonaws.com/M4-Hourly.csv')
test = pd.read_csv('https://auto-arima-results.s3.amazonaws.com/M4-Hourly-test.csv').rename(columns={'y': 'y_test'})

train.head()

test.head()

Since the goal of this notebook is to generate prediction intervals, we’ll only use the first 8 series of the dataset to reduce the total computational time.

n_series = 8 
uids = train['unique_id'].unique()[:n_series] # select first n_series of the dataset
train = train.query('unique_id in @uids')
test = test.query('unique_id in @uids')

We can plot these series using the statsforecast.plot method from the StatsForecast class. This method has multiple parameters, and the required ones to generate the plots in this notebook are explained below.

• df: A pandas dataframe with columns [unique_id, ds, y].
• forecasts_df: A pandas dataframe with columns [unique_id, ds] and models.
• plot_random: bool = True. Plots the time series randomly.
• models: List[str]. A list with the models we want to plot.
• level: List[float]. A list with the prediction intervals we want to plot.
• engine: str = plotly. It can also be matplotlib. plotly generates interactive plots, while matplotlib generates static plots.

from statsforecast import StatsForecast

StatsForecast.plot(train, test, plot_random=False)

​

Train models

StatsForecast can train multiple models on different time series efficiently. Most of these models can generate a probabilistic forecast, which means that they can produce both point forecasts and prediction intervals.

For this example, we’ll use AutoETS and the following baseline models:

• HistoricAverage
• Naive
• RandomWalkWithDrift
• SeasonalNaive

To use these models, we first need to import them from statsforecast.models and then we need to instantiate them. Given that we’re working with hourly data, we need to set seasonal_length=24 in the models that requiere this parameter.

from statsforecast.models import (
    AutoETS, 
    HistoricAverage, 
    Naive, 
    RandomWalkWithDrift, 
    SeasonalNaive
)

# Create a list of models and instantiation parameters 
models = [
    AutoETS(season_length=24),
    HistoricAverage(), 
    Naive(), 
    RandomWalkWithDrift(), 
    SeasonalNaive(season_length=24)
]

To instantiate a new StatsForecast object, we need the following parameters:

• df: The dataframe with the training data.
• models: The list of models defined in the previous step.
• freq: A string indicating the frequency of the data. See pandas’ available frequencies.
• n_jobs: An integer that indicates the number of jobs used in parallel processing. Use -1 to select all cores.

sf = StatsForecast( 
    models=models, 
    freq=1,
    n_jobs=-1
)

Now we’re ready to generate the point forecasts and the prediction intervals. To do this, we’ll use the forecast method, which takes two arguments:

• h: An integer that represent the forecasting horizon. In this case, we’ll forecast the next 48 hours.
• level: A list of floats with the confidence levels of the prediction intervals. For example, level=[95] means that the range of values should include the actual future value with probability 95%.

levels = [80, 90, 95, 99] # confidence levels of the prediction intervals 

forecasts = sf.forecast(df=train, h=48, level=levels)
forecasts.head()

We’ll now merge the forecasts and their prediction intervals with the test set. This will allow us generate the plots of each probabilistic model.

test = test.merge(forecasts, how='left', on=['unique_id', 'ds'])

​

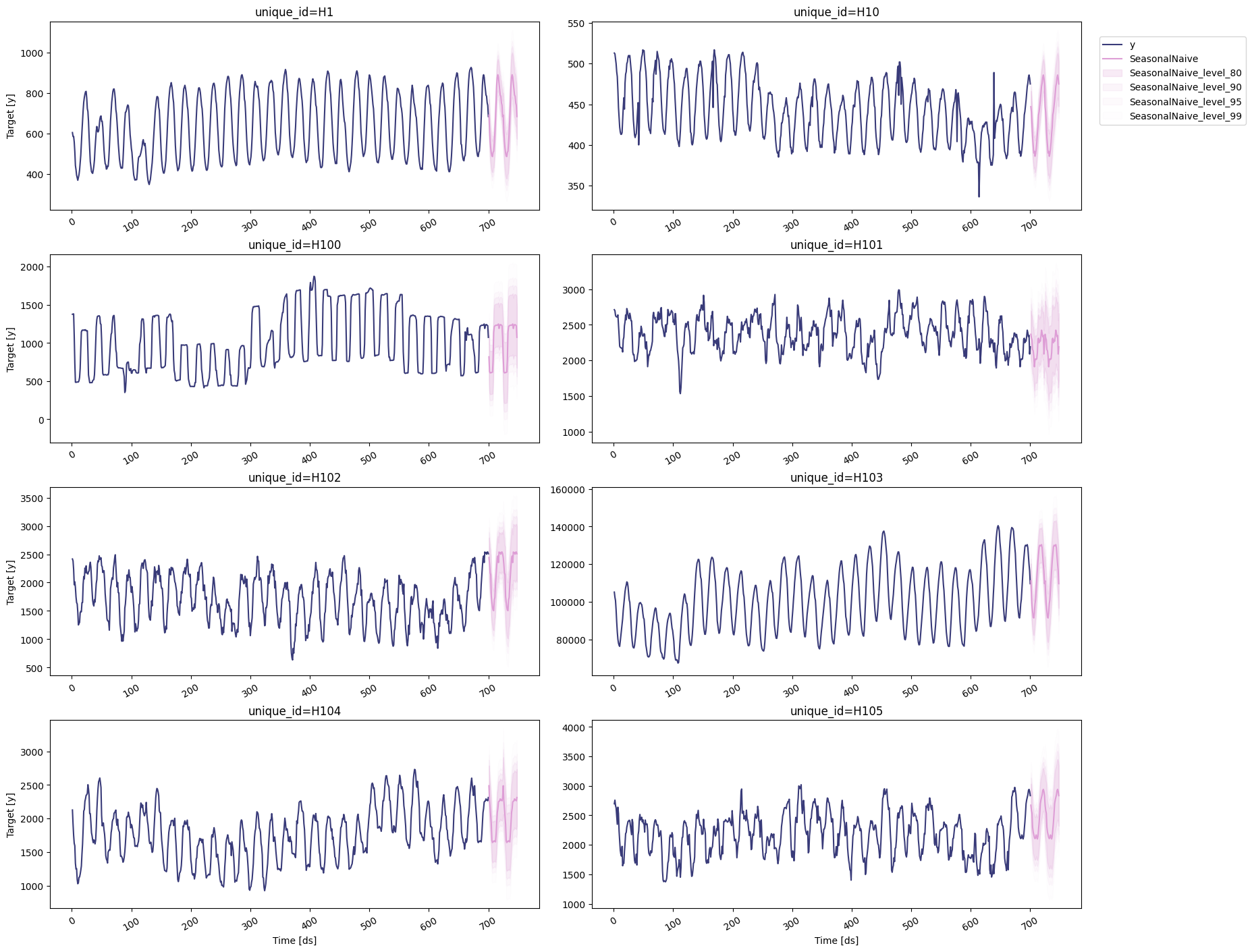
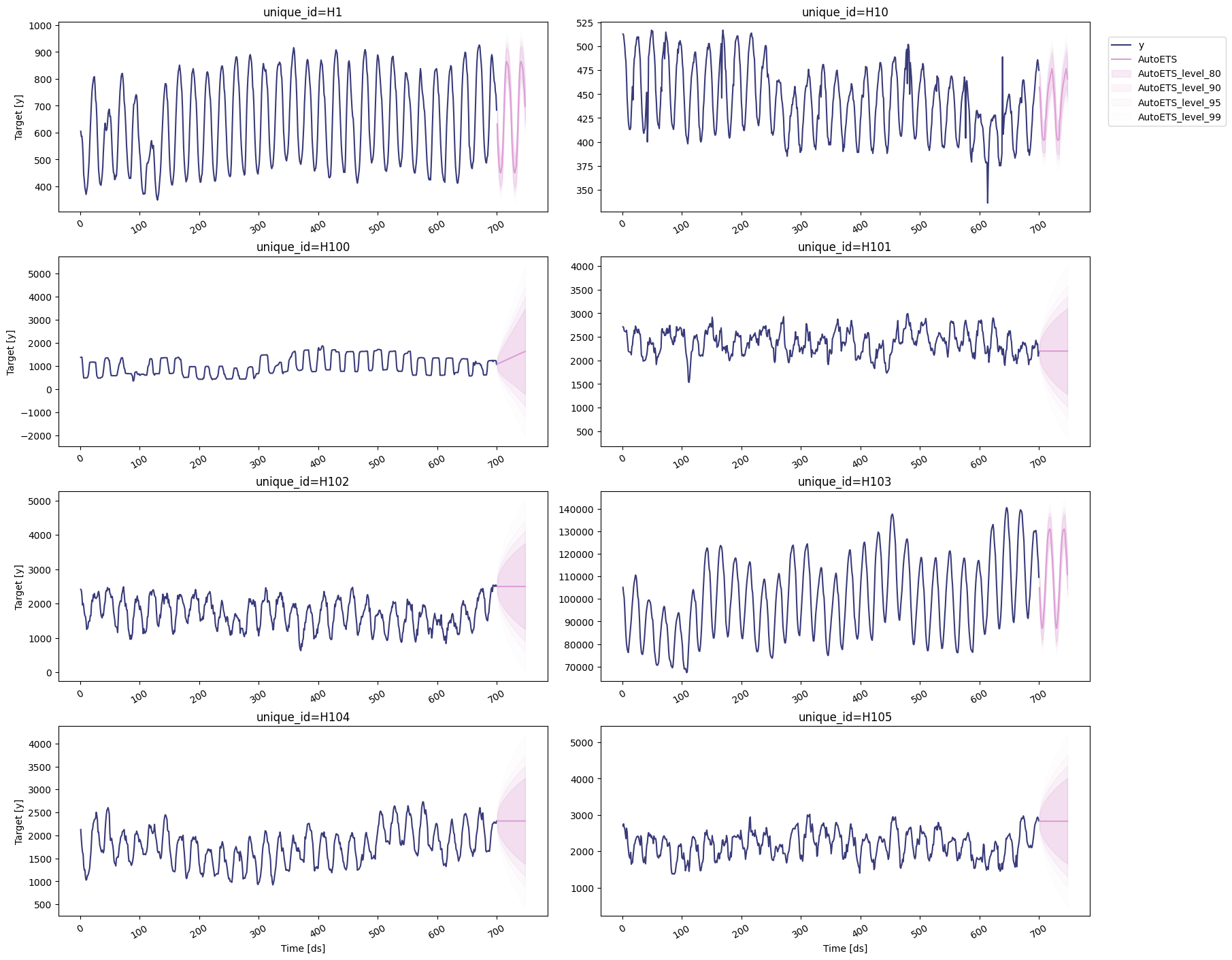
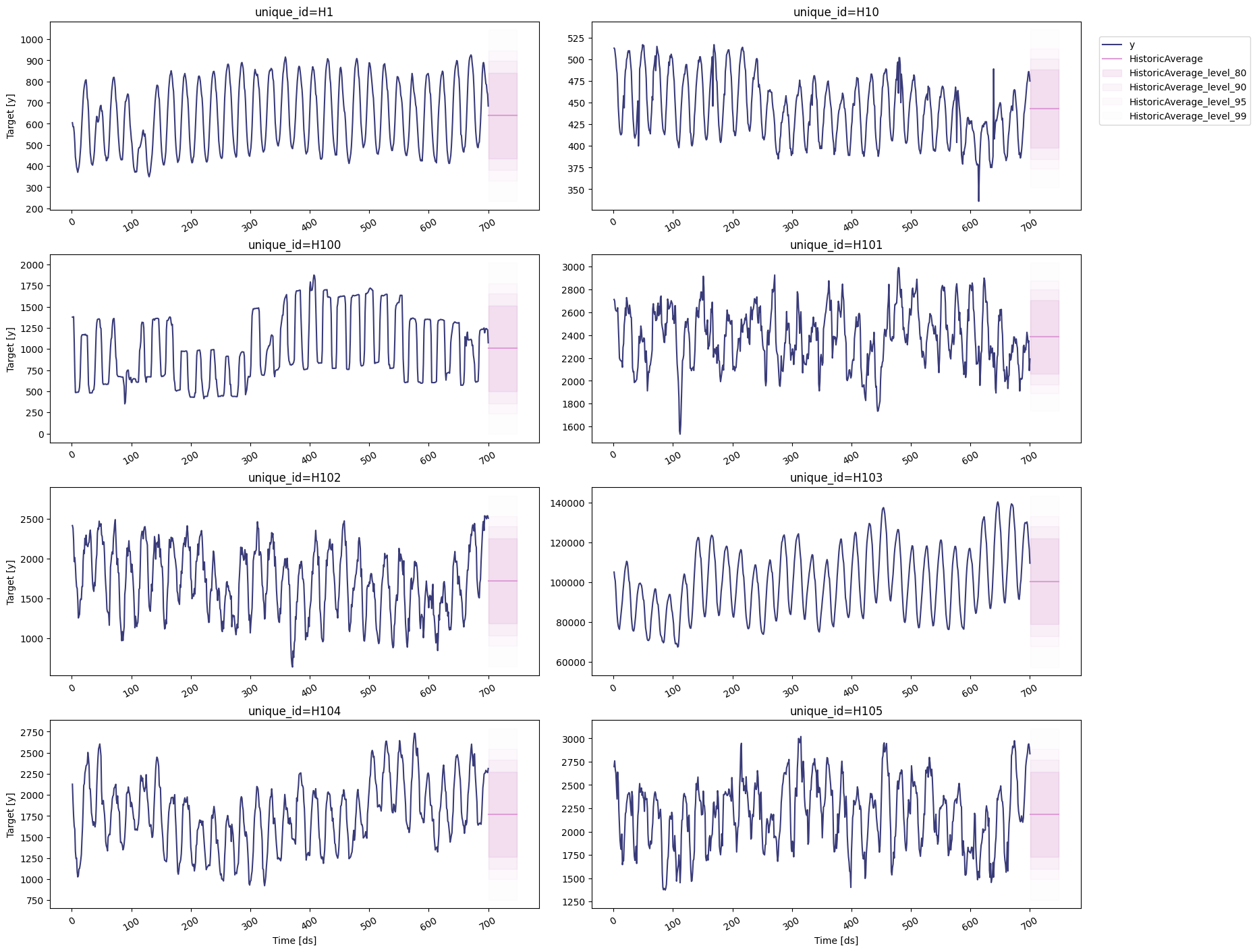
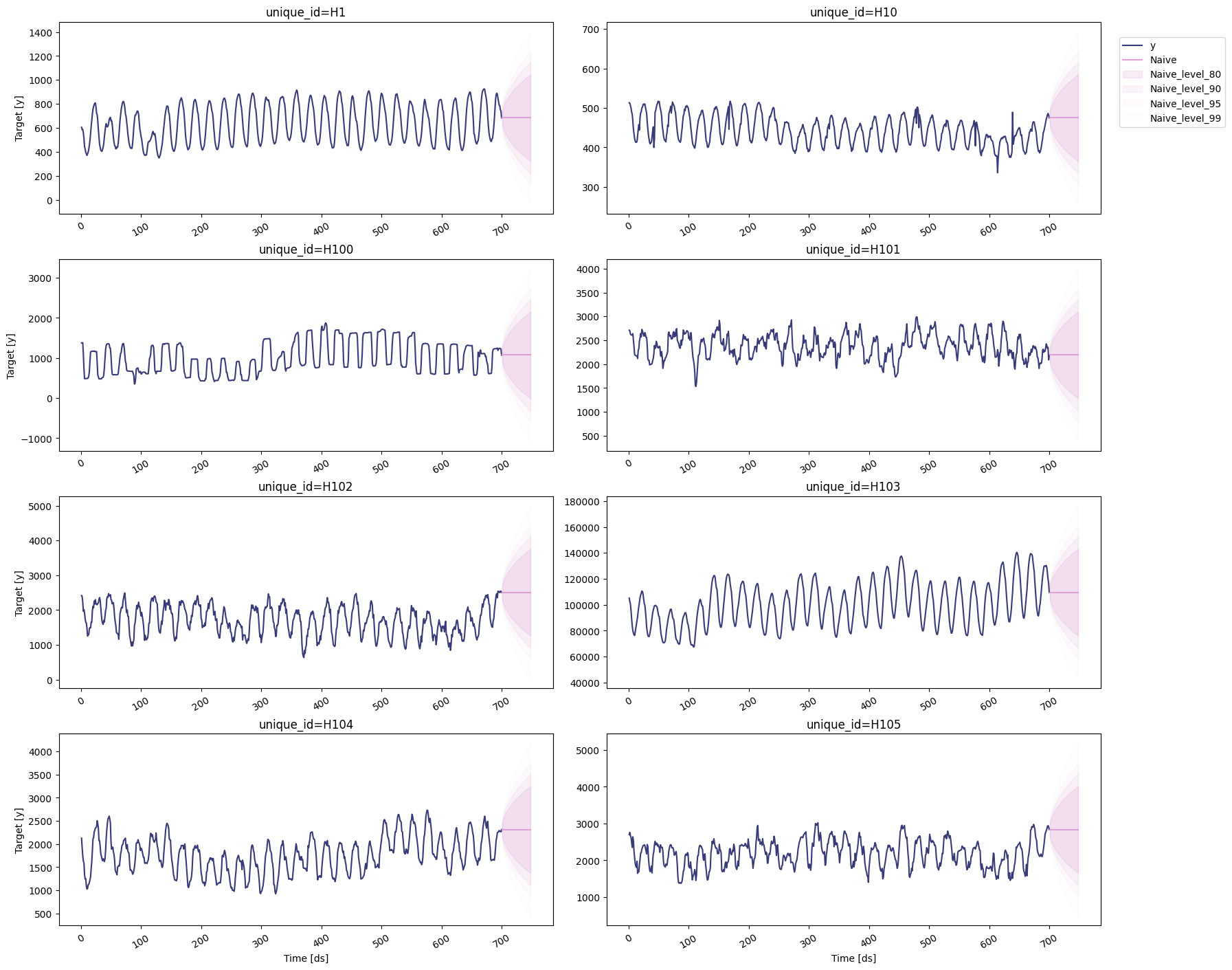
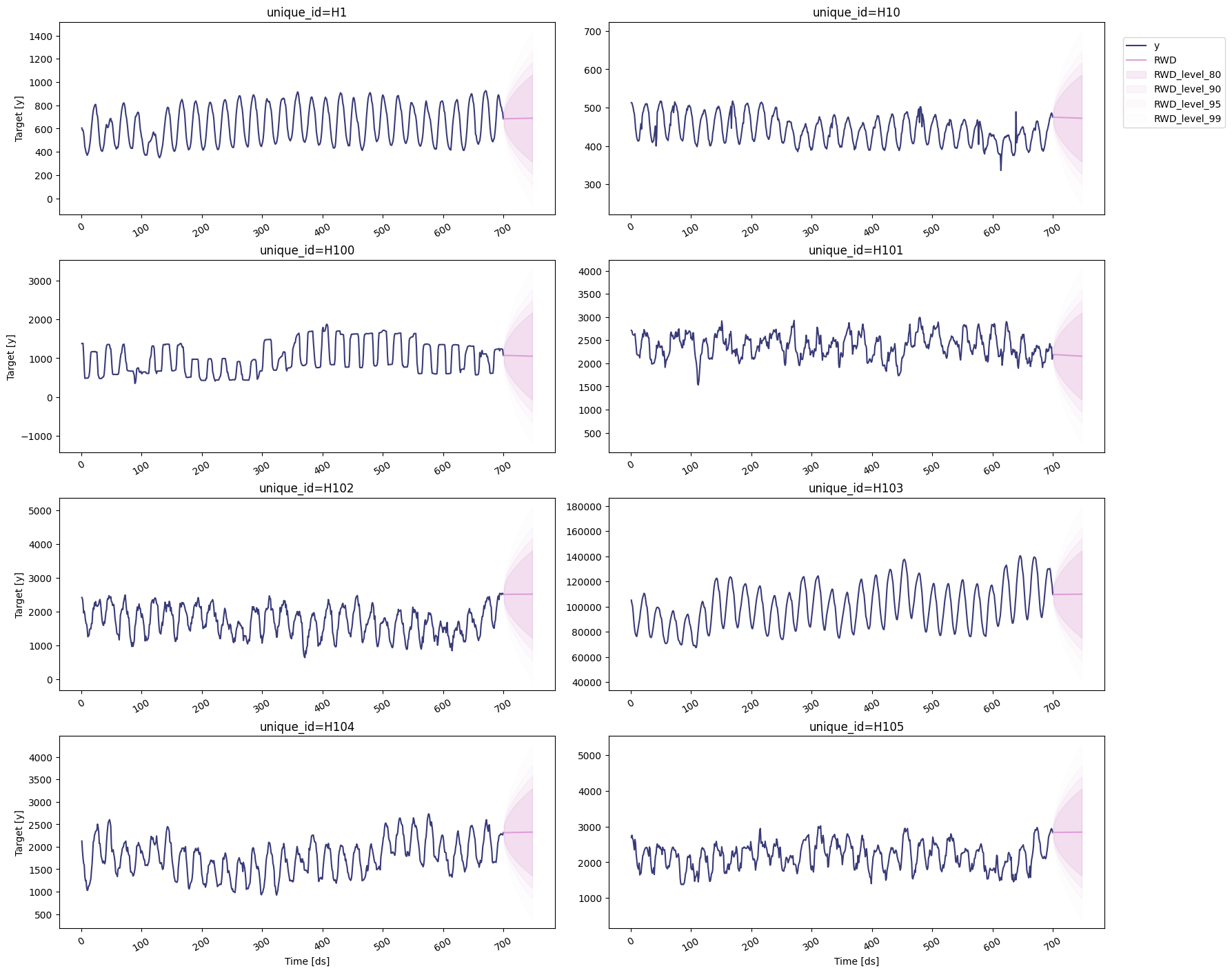
Plot prediction intervals

To plot the point and the prediction intervals, we’ll use the statsforecast.plot method again. Notice that now we also need to specify the model and the levels that we want to plot.

​

AutoETS

sf.plot(train, test, plot_random=False, models=['AutoETS'], level=levels)

​

Historic Average

sf.plot(train, test, plot_random=False, models=['HistoricAverage'], level=levels)

​

Naive

sf.plot(train, test, plot_random=False, models=['Naive'], level=levels)

​

Random Walk with Drift

sf.plot(train, test, plot_random=False, models=['RWD'], level=levels)

​

Seasonal Naive

sf.plot(train, test, plot_random=False, models=['SeasonalNaive'], level=levels)

From these plots, we can conclude that the uncertainty around each forecast varies according to the model that is being used. For the same time series, one model can predict a wider range of possible future values than others.

​

References

Rob J. Hyndman and George Athanasopoulos (2018). “Forecasting principles and practice, The Statistical Forecasting Perspective”.