Model training, evaluation and selection for multiple time series
Prerequisites This Guide assumes basic familiarity with StatsForecast. For a minimal example visit the Quick Start.Follow this article for a step-by-step guide on building a production-ready forecasting pipeline for multiple time series. During this guide you will gain familiarity with the core
StatsForecastclass and some relevant methods like
StatsForecast.plot, StatsForecast.forecast and
StatsForecast.cross_validation.
We will use a classical benchmarking dataset from the M4 competition.
The dataset includes time series from different domains like finance,
economy and sales. In this example, we will use a subset of the Hourly
dataset.
We will model each time series individually. Forecasting at this level
is also known as local forecasting. Therefore, you will train a series
of models for every unique series and then select the best one.
StatsForecast focuses on speed, simplicity, and scalability, which makes
it ideal for this task.
Outline:
- Install packages.
- Read the data.
- Explore the data.
- Train many models for every unique combination of time series.
- Evaluate the model’s performance using cross-validation.
- Select the best model for every unique time series.
Not Covered in this guide
- Forecasting at scale using clusters on the cloud.
- Forecast the M5 Dataset in 5min using Ray clusters.
- Forecast the M5 Dataset in 5min using Spark clusters.
- Learn how to predict 1M series in less than 30min.
- Training models on Multiple Seasonalities.
- Learn to use multiple seasonality in this Electricity Load forecasting tutorial.
- Using external regressors or exogenous variables
- Follow this tutorial to include exogenous variables like weather or holidays or static variables like category or family.
- Comparing StatsForecast with other popular libraries.
- You can reproduce our benchmarks here.
Install libraries
We assume you have StatsForecast already installed. Check this guide for instructions on how to install StatsForecast.Read the data
We will use pandas to read the M4 Hourly data set stored in a parquet file for efficiency. You can use ordinary pandas operations to read your data in other formats likes.csv.
The input to StatsForecast is always a data frame in long
format with
three columns: unique_id, ds and y:
-
The
unique_id(string, int or category) represents an identifier for the series. -
The
ds(datestamp or int) column should be either an integer indexing time or a datestamp ideally like YYYY-MM-DD for a date or YYYY-MM-DD HH:MM:SS for a timestamp. -
The
y(numeric) represents the measurement we wish to forecast. The target column needs to be renamed toyif it has a different column name.
| unique_id | ds | y | |
|---|---|---|---|
| 0 | H1 | 1 | 605.0 |
| 1 | H1 | 2 | 586.0 |
| 2 | H1 | 3 | 586.0 |
| 3 | H1 | 4 | 559.0 |
| 4 | H1 | 5 | 511.0 |
Note Processing time is dependent on the available computing resources. Running this example with the complete dataset takes around 10 minutes in a c5d.24xlarge (96 cores) instance from AWS.
Explore Data with the plot method
Plot some series using theplot method from the StatsForecast class.
This method prints 8 random series from the dataset and is useful for
basic EDA.
Note TheStatsForecast.plotmethod uses Plotly as a default engine. You can change to MatPlotLib by settingengine="matplotlib".

Train multiple models for many series
StatsForecast can train many models on many time series efficiently. Start by importing and instantiating the desired models. StatsForecast offers a wide variety of models grouped in the following categories:- Auto Forecast: Automatic forecasting tools search for the best parameters and select the best possible model for a series of time series. These tools are useful for large collections of univariate time series. Includes automatic versions of: Arima, ETS, Theta, CES.
- Exponential Smoothing: Uses a weighted average of all past observations where the weights decrease exponentially into the past. Suitable for data with no clear trend or seasonality. Examples: SES, Holt’s Winters, SSO.
- Benchmark models: classical models for establishing baselines. Examples: Mean, Naive, Random Walk
- Intermittent or Sparse models: suited for series with very few non-zero observations. Examples: CROSTON, ADIDA, IMAPA
- Multiple Seasonalities: suited for signals with more than one clear seasonality. Useful for low-frequency data like electricity and logs. Examples: MSTL.
- Theta Models: fit two theta lines to a deseasonalized time series, using different techniques to obtain and combine the two theta lines to produce the final forecasts. Examples: Theta, DynamicTheta
-
AutoARIMA: Automatically selects the best ARIMA (AutoRegressive Integrated Moving Average) model using an information criterion. Ref:AutoARIMA. -
HoltWinters: triple exponential smoothing, Holt-Winters’ method is an extension of exponential smoothing for series that contain both trend and seasonality. Ref:HoltWinters -
SeasonalNaive: Memory Efficient Seasonal Naive predictions. Ref:SeasonalNaive -
HistoricAverage: arithmetic mean. Ref:HistoricAverage. -
DynamicOptimizedTheta: The theta family of models has been shown to perform well in various datasets such as M3. Models the deseasonalized time series. Ref:DynamicOptimizedTheta.
season_length argument
is sometimes tricky. This article on Seasonal
periods) by the
master, Rob Hyndmann, can be useful.
StatsForecast object with the
following parameters:
-
models: a list of models. Select the models you want from models and import them. -
freq: a string indicating the frequency of the data. (See pandas available frequencies.) -
n_jobs: int, number of jobs used in the parallel processing, use -1 for all cores. -
fallback_model: a model to be used if a model fails.
Note StatsForecast achieves its blazing speed using JIT compiling through Numba. The first time you call the statsforecast class, the fit method should take around 5 seconds. The second time -once Numba compiled your settings- it should take less than 0.2s.The
forecast method takes two arguments: forecasts next h (horizon)
and level.
-
h(int): represents the forecast h steps into the future. In this case, 12 months ahead. -
level(list of floats): this optional parameter is used for probabilistic forecasting. Set thelevel(or confidence percentile) of your prediction interval. For example,level=[90]means that the model expects the real value to be inside that interval 90% of the times.
Note Theforecastmethod is compatible with distributed clusters, so it does not store any model parameters. If you want to store parameters for every model you can use thefitandpredictmethods. However, those methods are not defined for distributed engines like Spark, Ray or Dask.
| unique_id | ds | HoltWinters | HoltWinters-lo-90 | HoltWinters-hi-90 | CrostonClassic | CrostonClassic-lo-90 | CrostonClassic-hi-90 | SeasonalNaive | SeasonalNaive-lo-90 | SeasonalNaive-hi-90 | HistoricAverage | HistoricAverage-lo-90 | HistoricAverage-hi-90 | DynamicOptimizedTheta | DynamicOptimizedTheta-lo-90 | DynamicOptimizedTheta-hi-90 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | H1 | 749 | 829.0 | 422.549268 | 1235.450732 | 829.0 | 422.549268 | 1235.450732 | 635.0 | 566.036734 | 703.963266 | 660.982143 | 398.037761 | 923.926524 | 592.701851 | 577.677280 | 611.652639 |
| 1 | H1 | 750 | 807.0 | 400.549268 | 1213.450732 | 807.0 | 400.549268 | 1213.450732 | 572.0 | 503.036734 | 640.963266 | 660.982143 | 398.037761 | 923.926524 | 525.589116 | 505.449755 | 546.621805 |
| 2 | H1 | 751 | 785.0 | 378.549268 | 1191.450732 | 785.0 | 378.549268 | 1191.450732 | 532.0 | 463.036734 | 600.963266 | 660.982143 | 398.037761 | 923.926524 | 489.251814 | 462.072871 | 512.424116 |
| 3 | H1 | 752 | 756.0 | 349.549268 | 1162.450732 | 756.0 | 349.549268 | 1162.450732 | 493.0 | 424.036734 | 561.963266 | 660.982143 | 398.037761 | 923.926524 | 456.195032 | 430.554302 | 478.260963 |
| 4 | H1 | 753 | 719.0 | 312.549268 | 1125.450732 | 719.0 | 312.549268 | 1125.450732 | 477.0 | 408.036734 | 545.963266 | 660.982143 | 398.037761 | 923.926524 | 436.290514 | 411.051232 | 461.815932 |
StatsForecast.plot
method.

StatsForecast.plot allows for further customization. For example,
plot the results of the different models and unique ids.


Evaluate the model’s performance
In previous steps, we’ve taken our historical data to predict the future. However, to assess its accuracy we would also like to know how the model would have performed in the past. To assess the accuracy and robustness of your models on your data perform Cross-Validation. With time series data, Cross Validation is done by defining a sliding window across the historical data and predicting the period following it. This form of cross-validation allows us to arrive at a better estimation of our model’s predictive abilities across a wider range of temporal instances while also keeping the data in the training set contiguous as is required by our models. The following graph depicts such a Cross Validation Strategy: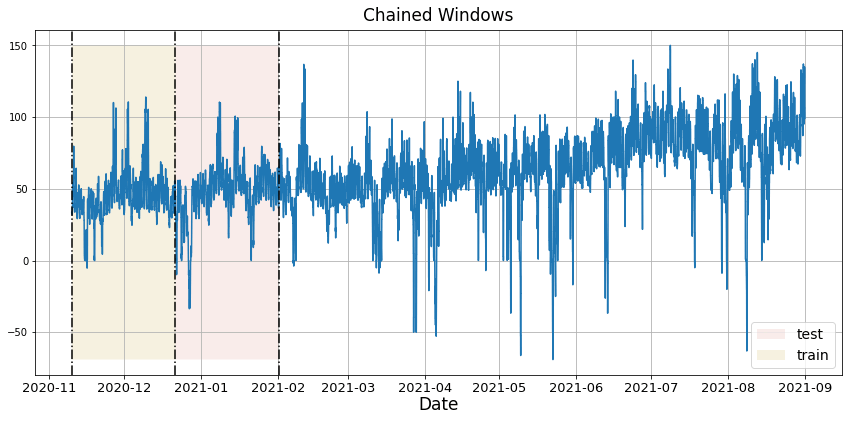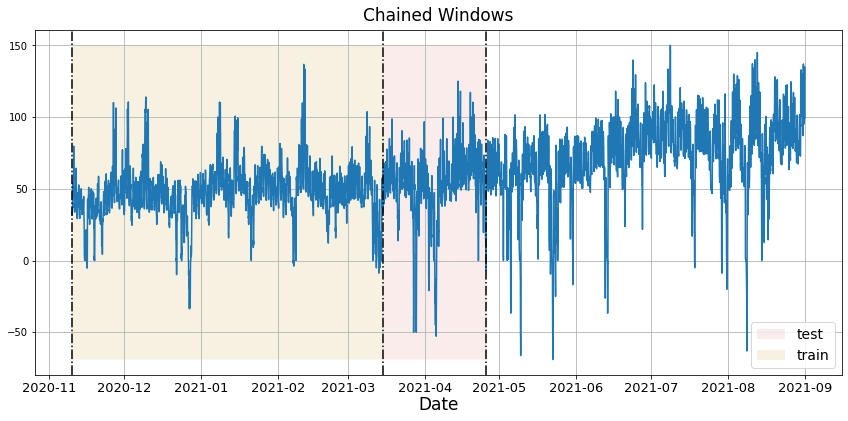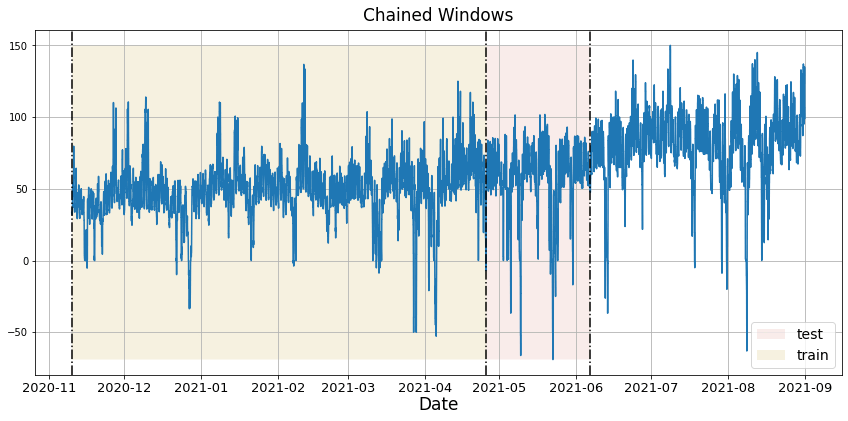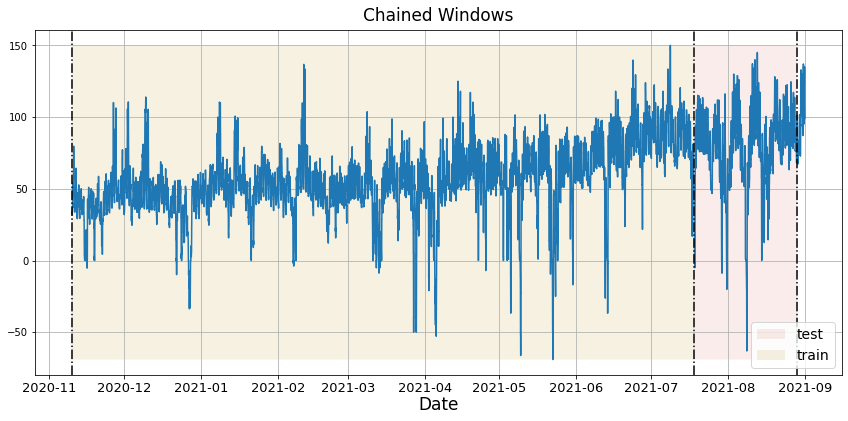 Cross-validation of time series models is considered a best practice but
most implementations are very slow. The statsforecast library implements
cross-validation as a distributed operation, making the process less
time-consuming to perform. If you have big datasets you can also perform
Cross Validation in a distributed cluster using Ray, Dask or Spark.
In this case, we want to evaluate the performance of each model for the
last 2 days (n_windows=2), forecasting every second day (step_size=48).
Depending on your computer, this step should take around 1 min.
Cross-validation of time series models is considered a best practice but
most implementations are very slow. The statsforecast library implements
cross-validation as a distributed operation, making the process less
time-consuming to perform. If you have big datasets you can also perform
Cross Validation in a distributed cluster using Ray, Dask or Spark.
In this case, we want to evaluate the performance of each model for the
last 2 days (n_windows=2), forecasting every second day (step_size=48).
Depending on your computer, this step should take around 1 min.
Tip
Setting n_windows=1 mirrors a traditional train-test split with our
historical data serving as the training set and the last 48 hours
serving as the testing set.
The cross_validation method from the StatsForecast class takes the
following arguments.
-
df: training data frame -
h(int): represents h steps into the future that are being forecasted. In this case, 24 hours ahead. -
step_size(int): step size between each window. In other words: how often do you want to run the forecasting processes. -
n_windows(int): number of windows used for cross validation. In other words: what number of forecasting processes in the past do you want to evaluate.
cv_df object is a new data frame that includes the following
columns:
-
unique_id: series identifier -
ds: datestamp or temporal index -
cutoff: the last datestamp or temporal index for then_windows.Ifn_windows=1, then one unique cutoff value, ifn_windows=2then two unique cutoff values. -
y: true value -
"model": columns with the model’s name and fitted value.
| unique_id | ds | cutoff | y | HoltWinters | CrostonClassic | SeasonalNaive | HistoricAverage | DynamicOptimizedTheta | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | H1 | 701 | 700 | 619.0 | 847.0 | 742.668748 | 691.0 | 661.675 | 612.767504 |
| 1 | H1 | 702 | 700 | 565.0 | 820.0 | 742.668748 | 618.0 | 661.675 | 536.846278 |
| 2 | H1 | 703 | 700 | 532.0 | 790.0 | 742.668748 | 563.0 | 661.675 | 497.824286 |
| 3 | H1 | 704 | 700 | 495.0 | 784.0 | 742.668748 | 529.0 | 661.675 | 464.723219 |
| 4 | H1 | 705 | 700 | 481.0 | 752.0 | 742.668748 | 504.0 | 661.675 | 440.972336 |
utilsforecast.losses. Then
define a utility function that takes a cross-validation data frame as a
metric and returns an evaluation data frame with the average of the
error metric for every unique id and fitted model and all cutoffs.
Warning You can also use Mean Average Percentage Error (MAPE), however for granular forecasts, MAPE values are extremely hard to judge and not useful to assess forecasting quality.Create the data frame with the results of the evaluation of your cross-validation data frame using a Mean Squared Error metric.
| unique_id | HoltWinters | CrostonClassic | SeasonalNaive | HistoricAverage | DynamicOptimizedTheta | best_model | |
|---|---|---|---|---|---|---|---|
| 0 | H1 | 44888.020833 | 28038.733985 | 1422.666667 | 20927.664488 | 1296.333977 | DynamicOptimizedTheta |
| 1 | H10 | 2812.916667 | 1483.483839 | 96.895833 | 1980.367543 | 379.621134 | SeasonalNaive |
| 2 | H100 | 121625.375000 | 91945.139237 | 12019.000000 | 78491.191439 | 21699.649325 | SeasonalNaive |
| 3 | H101 | 28453.395833 | 16183.634340 | 10944.458333 | 18208.409800 | 63698.077266 | SeasonalNaive |
| 4 | H102 | 232924.854167 | 132655.309136 | 12699.895833 | 309110.475212 | 31393.535274 | SeasonalNaive |
| best_model | count | |
|---|---|---|
| 0 | SeasonalNaive | 6 |
| 1 | DynamicOptimizedTheta | 4 |

Select the best model for every unique series
Define a utility function that takes your forecast’s data frame with the predictions and the evaluation data frame and returns a data frame with the best possible forecast for every unique_id.| unique_id | ds | best_model | best_model-lo-90 | best_model-hi-90 | |
|---|---|---|---|---|---|
| 0 | H1 | 749 | 592.701851 | 577.677280 | 611.652639 |
| 1 | H1 | 750 | 525.589116 | 505.449755 | 546.621805 |
| 2 | H1 | 751 | 489.251814 | 462.072871 | 512.424116 |
| 3 | H1 | 752 | 456.195032 | 430.554302 | 478.260963 |
| 4 | H1 | 753 | 436.290514 | 411.051232 | 461.815932 |


