Skip to main content
In this example we will show how to perform electricity load forecasting considering a model capable of handling multiple seasonalities (MSTL).
Open In Colab

​
Introduction

Some time series are generated from very low frequency data. These data generally exhibit multiple seasonalities. For example, hourly data may exhibit repeated patterns every hour (every 24 observations) or every day (every 24 * 7, hours per day, observations). This is the case for electricity load. Electricity load may vary hourly, e.g., during the evenings electricity consumption may be expected to increase. But also, the electricity load varies by week. Perhaps on weekends there is an increase in electrical activity. In this example we will show how to model the two seasonalities of the time series to generate accurate forecasts in a short time. We will use hourly PJM electricity load data. The original data can be found here.

​
Libraries

In this example we will use the following libraries:
  • StatsForecast. Lightning ⚡️ fast forecasting with statistical and econometric models. Includes the MSTL model for multiple seasonalities.
  • Prophet. Benchmark model developed by Facebook.
  • NeuralProphet. Deep Learning version of Prophet. Used as benchark.
# !pip install statsforecast "neuralprophet[live]" prophet

​
Forecast using Multiple Seasonalities

​
Electricity Load Data

According to the dataset’s page,
PJM Interconnection LLC (PJM) is a regional transmission organization (RTO) in the United States. It is part of the Eastern Interconnection grid operating an electric transmission system serving all or parts of Delaware, Illinois, Indiana, Kentucky, Maryland, Michigan, New Jersey, North Carolina, Ohio, Pennsylvania, Tennessee, Virginia, West Virginia, and the District of Columbia. The hourly power consumption data comes from PJM’s website and are in megawatts (MW).
Let’s take a look to the data. 
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from utilsforecast.plotting import plot_series

pd.plotting.register_matplotlib_converters()
plt.rc("figure", figsize=(10, 8))
plt.rc("font", size=10)

df = pd.read_csv('https://raw.githubusercontent.com/panambY/Hourly_Energy_Consumption/master/data/PJM_Load_hourly.csv')
df.columns = ['ds', 'y']
df.insert(0, 'unique_id', 'PJM_Load_hourly')
df['ds'] = pd.to_datetime(df['ds'])
df = df.sort_values(['unique_id', 'ds']).reset_index(drop=True)
df.tail()
unique_iddsy
32891PJM_Load_hourly2001-12-31 20:00:0036392.0
32892PJM_Load_hourly2001-12-31 21:00:0035082.0
32893PJM_Load_hourly2001-12-31 22:00:0033890.0
32894PJM_Load_hourly2001-12-31 23:00:0032590.0
32895PJM_Load_hourly2002-01-01 00:00:0031569.0
plot_series(df)
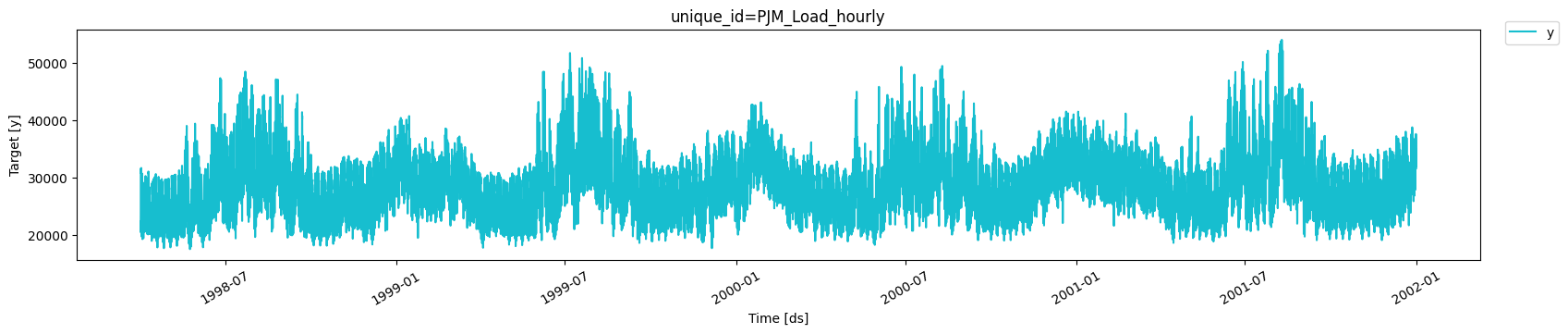
We clearly observe that the time series exhibits seasonal patterns. Moreover, the time series contains 32,896 observations, so it is necessary to use very computationally efficient methods to display them in production.

​
MSTL model

The MSTL (Multiple Seasonal-Trend decomposition using LOESS) model, originally developed by Kasun Bandara, Rob J Hyndman and Christoph Bergmeir, decomposes the time series in multiple seasonalities using a Local Polynomial Regression (LOESS). Then it forecasts the trend using a custom non-seasonal model and each seasonality using a SeasonalNaive model. StatsForecast contains a fast implementation of the MSTL model. Also, the decomposition of the time series can be calculated. 
from statsforecast import StatsForecast
from statsforecast.models import MSTL, AutoARIMA, SeasonalNaive
from statsforecast.utils import AirPassengers as ap
First we must define the model parameters. As mentioned before, the electricity load presents seasonalities every 24 hours (Hourly) and every 24 * 7 (Daily) hours. Therefore, we will use [24, 24 * 7] as the seasonalities that the MSTL model receives. We must also specify the manner in which the trend will be forecasted. In this case we will use the AutoARIMA model. 
mstl = MSTL(
    season_length=[24, 24 * 7], # seasonalities of the time series 
    trend_forecaster=AutoARIMA() # model used to forecast trend
)
Once the model is instantiated, we have to instantiate the StatsForecast class to create forecasts. 
sf = StatsForecast(
    models=[mstl], # model used to fit each time series 
    freq='h', # frequency of the data
)

​
Fit the model

Afer that, we just have to use the fit method to fit each model to each time series. 
sf = sf.fit(df=df)

​
Decompose the time series in multiple seasonalities

Once the model is fitted, we can access the decomposition using the fitted_ attribute of StatsForecast. This attribute stores all relevant information of the fitted models for each of the time series. In this case we are fitting a single model for a single time series, so by accessing the fitted_ location [0, 0] we will find the relevant information of our model. The MSTL class generates a model_ attribute that contains the way the series was decomposed. 
sf.fitted_[0, 0].model_
datatrendseasonal24seasonal168remainder
022259.025899.808157-4720.213546581.308595498.096794
121244.025900.349395-5433.168901571.780657205.038849
220651.025900.875973-5829.135728557.14264322.117112
320421.025901.387631-5704.092794597.696957-373.991794
420713.025901.884103-5023.324375922.564854-1088.124582
………………
3289136392.033329.0315774254.112720917.258336-2108.402633
3289235082.033355.0835763625.077164721.689136-2619.849876
3289333890.033381.1084092571.794472549.661529-2612.564409
3289432590.033407.105839796.356548361.956280-1975.418667
3289531569.033433.075723-1260.860917279.777069-882.991876
Let’s look graphically at the different components of the time series. 
sf.fitted_[0, 0].model_.tail(24 * 28).plot(subplots=True, grid=True)
plt.tight_layout()
plt.show()
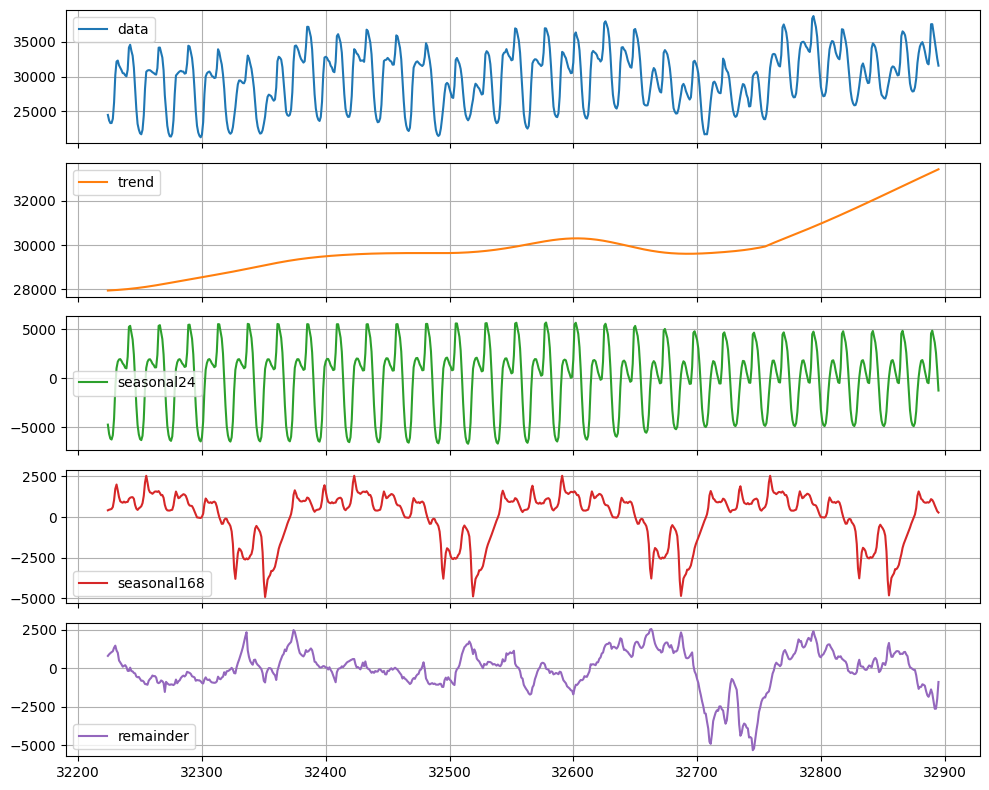
We observe that there is a clear trend towards the high (orange line). This component would be predicted with the AutoARIMA model. We can also observe that every 24 hours and every 24 * 7 hours there is a very well defined pattern. These two components will be forecast separately using a SeasonalNaive model.

​
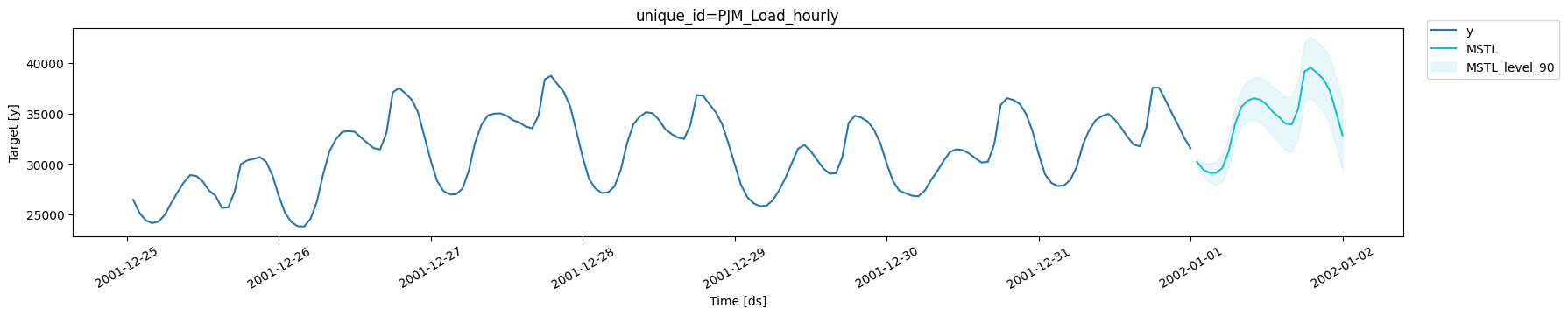
Produce forecasts

To generate forecasts we only have to use the predict method specifying the forecast horizon (h). In addition, to calculate prediction intervals associated to the forecasts, we can include the parameter level that receives a list of levels of the prediction intervals we want to build. In this case we will only calculate the 90% forecast interval (level=[90]). 
forecasts = sf.predict(h=24, level=[90])
forecasts.head()
unique_iddsMSTLMSTL-lo-90MSTL-hi-90
0PJM_Load_hourly2002-01-01 01:00:0030215.60816329842.18562230589.030705
1PJM_Load_hourly2002-01-01 02:00:0029447.20902828787.12336930107.294687
2PJM_Load_hourly2002-01-01 03:00:0029132.78760328221.35445430044.220751
3PJM_Load_hourly2002-01-01 04:00:0029126.25459127992.82142030259.687762
4PJM_Load_hourly2002-01-01 05:00:0029604.60867428273.42866330935.788686
Let’s look at our forecasts graphically. 
plot_series(df, forecasts, level=[90], max_insample_length=24*7)
In the next section we will plot different models so it is convenient to reuse the previous code with the following function. 
def plot_forecasts(y_hist, y_true, y_pred, models):
    _, ax = plt.subplots(1, 1, figsize = (20, 7))
    y_true = y_true.merge(y_pred, how='left', on=['unique_id', 'ds'])
    df_plot = pd.concat([y_hist, y_true]).set_index('ds').tail(24 * 7)
    df_plot[['y'] + models].plot(ax=ax, linewidth=2)
    colors = ['orange', 'green', 'red']
    for model, color in zip(models, colors):
        ax.fill_between(df_plot.index, 
                        df_plot[f'{model}-lo-90'], 
                        df_plot[f'{model}-hi-90'],
                        alpha=.35,
                        color=color,
                        label=f'{model}-level-90')
    ax.set_title('PJM Load Hourly', fontsize=22)
    ax.set_ylabel('Electricity Load', fontsize=20)
    ax.set_xlabel('Timestamp [t]', fontsize=20)
    ax.legend(prop={'size': 15})
    ax.grid()

​
Performance of the MSTL model

​
Split Train/Test sets

To validate the accuracy of the MSTL model, we will show its performance on unseen data. We will use a classical time series technique that consists of dividing the data into a training set and a test set. We will leave the last 24 observations (the last day) as the test set. So the model will train on 32,872 observations. 
df_test = df.tail(24)
df_train = df.drop(df_test.index)

​
MSTL model

In addition to the MSTL model, we will include the SeasonalNaive model as a benchmark to validate the added value of the MSTL model. Including StatsForecast models is as simple as adding them to the list of models to be fitted. 
sf = StatsForecast(
    models=[mstl, SeasonalNaive(season_length=24)], # add SeasonalNaive model to the list
    freq='h'
)
To measure the fitting time we will use the time module. 
from time import time
To retrieve the forecasts of the test set we only have to do fit and predict as before. 
init = time()
sf = sf.fit(df=df_train)
forecasts_test = sf.predict(h=len(df_test), level=[90])
end = time()
forecasts_test.head()
unique_iddsMSTLMSTL-lo-90MSTL-hi-90SeasonalNaiveSeasonalNaive-lo-90SeasonalNaive-hi-90
0PJM_Load_hourly2001-12-31 01:00:0029158.87218028785.56787529532.17648628326.023468.55587233183.444128
1PJM_Load_hourly2001-12-31 02:00:0028233.45226327573.78908928893.11543827362.022504.55587232219.444128
2PJM_Load_hourly2001-12-31 03:00:0027915.25136827004.45900028826.04373627108.022250.55587231965.444128
3PJM_Load_hourly2001-12-31 04:00:0027969.39656026836.67416429102.11895626865.022007.55587231722.444128
4PJM_Load_hourly2001-12-31 05:00:0028469.80558827139.30640129800.30477526808.021950.55587231665.444128
time_mstl = (end - init) / 60
print(f'MSTL Time: {time_mstl:.2f} minutes')

MSTL Time: 0.46 minutes
Then we were able to generate forecasts for the next 24 hours. Now let’s look at the graphical comparison of the forecasts with the actual values. 
plot_series(df_train, df_test.merge(forecasts_test), level=[90], max_insample_length=24*7)
Let’s look at those produced only by MSTL. 
plot_series(df_train, df_test.merge(forecasts_test), level=[90], max_insample_length=24*7, models=['MSTL'])
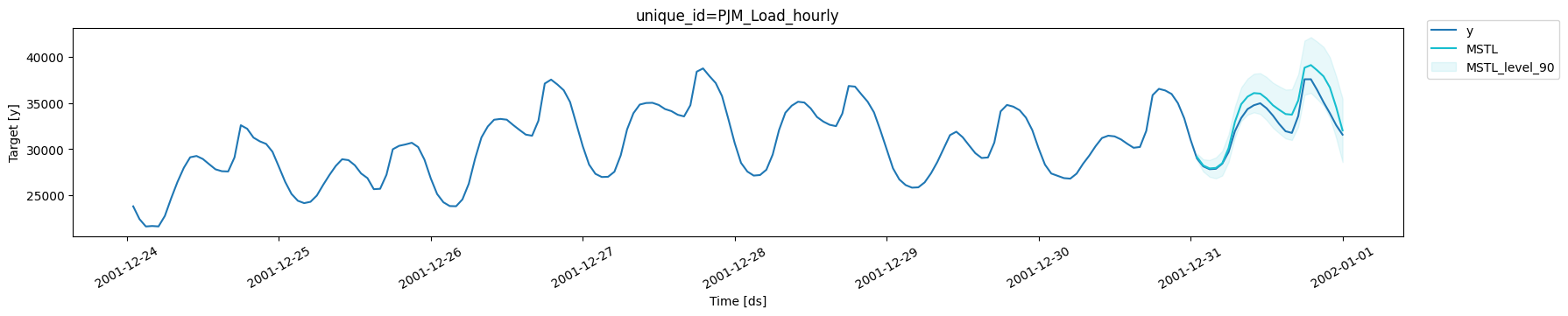
We note that MSTL produces very accurate forecasts that follow the behavior of the time series. Now let us calculate numerically the accuracy of the model. We will use the following metrics: MAE, MAPE, MASE, RMSE, SMAPE. 
from functools import partial

from utilsforecast.evaluation import evaluate
from utilsforecast.losses import mae, mape, mase, rmse, smape

eval_df = evaluate(
    df=df_test.merge(forecasts_test),
    train_df=df_train,
    metrics=[partial(mase, seasonality=24), mae, mape, rmse, smape],
    agg_fn='mean',
).set_index('metric').T
eval_df
metricmasemaemapermsesmape
MSTL0.5872651219.3217950.0360521460.2232790.017577
SeasonalNaive0.8946531857.5416670.0564822201.3841010.029343
1 - eval_df.loc['MSTL', 'mase'] / eval_df.loc['SeasonalNaive', 'mase']

0.3435830717111049
We observe that MSTL has an improvement of about 35% over the SeasonalNaive method in the test set measured in MASE.

​
Comparison with Prophet

One of the most widely used models for time series forecasting is Prophet. This model is known for its ability to model different seasonalities (weekly, daily yearly). We will use this model as a benchmark to see if the MSTL adds value for this time series. 
from prophet import Prophet

# create prophet model
prophet = Prophet(interval_width=0.9)
init = time()
prophet.fit(df_train)
# produce forecasts
future = prophet.make_future_dataframe(periods=len(df_test), freq='H', include_history=False)
forecast_prophet = prophet.predict(future)
end = time()
# data wrangling
forecast_prophet = forecast_prophet[['ds', 'yhat', 'yhat_lower', 'yhat_upper']]
forecast_prophet.columns = ['ds', 'Prophet', 'Prophet-lo-90', 'Prophet-hi-90']
forecast_prophet.insert(0, 'unique_id', 'PJM_Load_hourly')
forecast_prophet.head()

16:56:47 - cmdstanpy - INFO - Chain [1] start processing
16:57:09 - cmdstanpy - INFO - Chain [1] done processing
unique_iddsProphetProphet-lo-90Prophet-hi-90
0PJM_Load_hourly2001-12-31 01:00:0025294.24696020299.10576630100.467618
1PJM_Load_hourly2001-12-31 02:00:0024000.72542319285.39514428777.495372
2PJM_Load_hourly2001-12-31 03:00:0023324.77196618536.73630628057.063589
3PJM_Load_hourly2001-12-31 04:00:0023332.51987118591.87919028720.461289
4PJM_Load_hourly2001-12-31 05:00:0024107.12682718934.47125429116.352931
time_prophet = (end - init) / 60
print(f'Prophet Time: {time_prophet:.2f} minutes')

Prophet Time: 0.41 minutes

times = pd.DataFrame({'model': ['MSTL', 'Prophet'], 'time (mins)': [time_mstl, time_prophet]})
times
modeltime (mins)
0MSTL0.455999
1Prophet0.408726
We observe that the time required for Prophet to perform the fit and predict pipeline is greater than MSTL. Let’s look at the forecasts produced by Prophet. 
forecasts_test = forecasts_test.merge(forecast_prophet, how='left', on=['unique_id', 'ds'])

plot_series(df_train, forecasts_test, max_insample_length=24*7, level=[90])
We note that Prophet is able to capture the overall behavior of the time series. However, in some cases it produces forecasts well below the actual value. It also does not correctly adjust the valleys. 
eval_df = evaluate(
    df=df_test.merge(forecasts_test),
    train_df=df_train,
    metrics=[partial(mase, seasonality=24), mae, mape, rmse, smape],
    agg_fn='mean',
).set_index('metric').T
eval_df
metricmasemaemapermsesmape
MSTL0.5872651219.3217950.0360521460.2232790.017577
SeasonalNaive0.8946531857.5416670.0564822201.3841010.029343
Prophet1.0995512282.9669770.0737502721.8172030.038633
1 - eval_df.loc['MSTL', 'mase'] / eval_df.loc['Prophet', 'mase']

0.4659047602697266
In terms of accuracy, Prophet is not able to produce better forecasts than the SeasonalNaive model, however, the MSTL model improves Prophet’s forecasts by 45% (MASE).

​
Comparison with NeuralProphet

NeuralProphet is the version of Prophet using deep learning. This model is also capable of handling different seasonalities so we will also use it as a benchmark. 
from neuralprophet import NeuralProphet

neuralprophet = NeuralProphet(quantiles=[0.05, 0.95])
init = time()
neuralprophet.fit(df_train.drop(columns='unique_id'))
future = neuralprophet.make_future_dataframe(df=df_train.drop(columns='unique_id'), periods=len(df_test))
forecast_np = neuralprophet.predict(future)
end = time()
forecast_np = forecast_np[['ds', 'yhat1', 'yhat1 5.0%', 'yhat1 95.0%']]
forecast_np.columns = ['ds', 'NeuralProphet', 'NeuralProphet-lo-90', 'NeuralProphet-hi-90']
forecast_np.insert(0, 'unique_id', 'PJM_Load_hourly')
forecast_np.head()

WARNING - (NP.forecaster.fit) - When Global modeling with local normalization, metrics are displayed in normalized scale.
INFO - (NP.df_utils._infer_frequency) - Major frequency h corresponds to 99.973% of the data.
INFO - (NP.df_utils._infer_frequency) - Dataframe freq automatically defined as h
INFO - (NP.config.init_data_params) - Setting normalization to global as only one dataframe provided for training.
INFO - (NP.config.set_auto_batch_epoch) - Auto-set batch_size to 128
INFO - (NP.config.set_auto_batch_epoch) - Auto-set epochs to 40
WARNING - (NP.config.set_lr_finder_args) - Learning rate finder: The number of batches (257) is too small than the required number                     for the learning rate finder (262). The results might not be optimal.
INFO - (NP.df_utils._infer_frequency) - Major frequency h corresponds to 99.973% of the data.
INFO - (NP.df_utils._infer_frequency) - Defined frequency is equal to major frequency - h
INFO - (NP.df_utils.return_df_in_original_format) - Returning df with no ID column
INFO - (NP.df_utils._infer_frequency) - Major frequency h corresponds to 95.833% of the data.
INFO - (NP.df_utils._infer_frequency) - Defined frequency is equal to major frequency - h
INFO - (NP.df_utils._infer_frequency) - Major frequency h corresponds to 95.833% of the data.
INFO - (NP.df_utils._infer_frequency) - Defined frequency is equal to major frequency - h
INFO - (NP.df_utils.return_df_in_original_format) - Returning df with no ID column

Training: |                                                                                                   …

Finding best initial lr:   0%|          | 0/262 [00:00<?, ?it/s]

Training: |                                                                                                   …

Predicting: |                                                                                                 …
unique_iddsNeuralProphetNeuralProphet-lo-90NeuralProphet-hi-90
0PJM_Load_hourly2001-12-31 01:00:0025292.38671922520.23828127889.425781
1PJM_Load_hourly2001-12-31 02:00:0024378.79687521640.46093827056.906250
2PJM_Load_hourly2001-12-31 03:00:0023852.91992220978.29101626583.130859
3PJM_Load_hourly2001-12-31 04:00:0023540.55468820700.03515626247.121094
4PJM_Load_hourly2001-12-31 05:00:0024016.58984421298.31640626748.933594
time_np = (end - init) / 60
print(f'Prophet Time: {time_np:.2f} minutes')

Prophet Time: 1.98 minutes

times = pd.concat([times, pd.DataFrame({'model': ['NeuralProphet'], 'time (mins)': [time_np]})])
times
modeltime (mins)
0MSTL0.455999
1Prophet0.408726
0NeuralProphet1.981253
We observe that NeuralProphet requires a longer processing time than Prophet and MSTL. 
forecasts_test = forecasts_test.merge(forecast_np, how='left', on=['unique_id', 'ds'])

plot_series(df_train, forecasts_test, max_insample_length=24*7, level=[90])
The forecasts graph shows that NeuralProphet generates very similar results to Prophet, as expected. 
eval_df = evaluate(
    df=df_test.merge(forecasts_test),
    train_df=df_train,
    metrics=[partial(mase, seasonality=24), mae, mape, rmse, smape],
    agg_fn='mean',
).set_index('metric').T
eval_df
metricmasemaemapermsesmape
MSTL0.5872651219.3217950.0360521460.2232790.017577
SeasonalNaive0.8946531857.5416670.0564822201.3841010.029343
Prophet1.0995512282.9669770.0737502721.8172030.038633
NeuralProphet1.0611602203.2559410.0710602593.7084960.037108
1 - eval_df.loc['MSTL', 'mase'] / eval_df.loc['NeuralProphet', 'mase']

0.4465818643911057
With respect to numerical evaluation, NeuralProphet improves the results of Prophet, as expected, however, MSTL improves over NeuralProphet’s foreacasts by 44% (MASE).
Important The performance of NeuralProphet can be improved using hyperparameter optimization, which can increase the fitting time significantly. In this example we show its performance with the default version.

​
Conclusion

In this post we introduced MSTL, a model originally developed by Kasun Bandara, Rob Hyndman and Christoph Bergmeir capable of handling time series with multiple seasonalities. We also showed that for the PJM electricity load time series offers better performance in time and accuracy than the Prophet and NeuralProphet models.

​
References