A logistic regression analyzes the relationship between a binary target variable and its predictor variables to estimate the probability of the dependent variable taking the value 1. In the presence of temporal data where observations along time aren’t independent, the errors of the model will be correlated through time and incorporating autoregressive features or lags can capture temporal dependencies and enhance the predictive power of logistic regression.
NHITS’s inputs are static exogenous x(s)\mathbf{x}^{(s)}, historic exogenous x[:t](h)\mathbf{x}^{(h)}_{[:t]}, exogenous available at the time of the prediction x[:t+H](f)\mathbf{x}^{(f)}_{[:t+H]} and autorregresive features y[:t]\mathbf{y}_{[:t]}, each of these inputs is further decomposed into categorical and continuous. The network uses a multi-quantile regression to model the following conditional probability:P(y[t+1:t+H]∣  y[:t],  x[:t](h),  x[:t+H](f),  x(s))\mathbb{P}(\mathbf{y}_{[t+1:t+H]}|\;\mathbf{y}_{[:t]},\; \mathbf{x}^{(h)}_{[:t]},\; \mathbf{x}^{(f)}_{[:t+H]},\; \mathbf{x}^{(s)}) In this notebook we show how to fit NeuralForecast methods for binary sequences regression. We will: - Installing NeuralForecast. - Loading binary sequence data. - Fit and predict temporal classifiers. - Plot and evaluate predictions. You can run these experiments using GPU with Google Colab. Open In Colab

​
1. Installing NeuralForecast

!pip install neuralforecast

import numpy as np
import pandas as pd
from sklearn import datasets

import matplotlib.pyplot as plt
from neuralforecast import NeuralForecast
from neuralforecast.models import MLP, NHITS, LSTM
from neuralforecast.losses.pytorch import DistributionLoss, Accuracy

​
2. Loading Binary Sequence Data

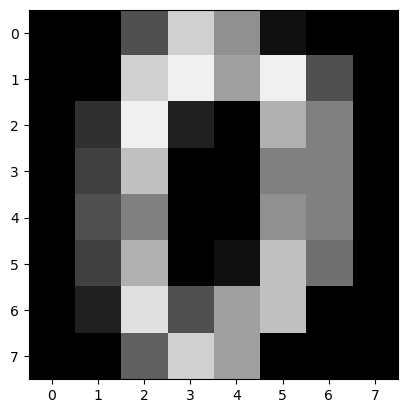
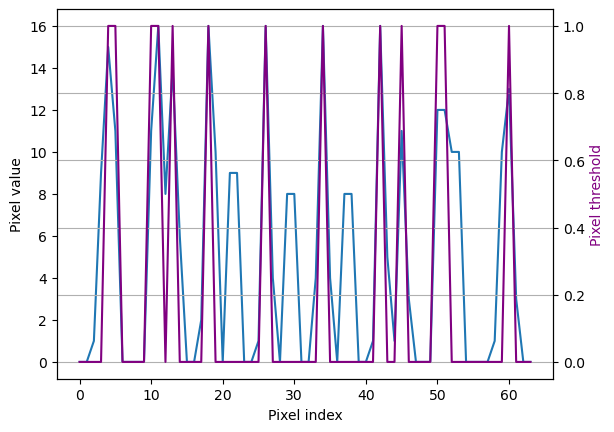
The core.NeuralForecast class contains shared, fit, predict and other methods that take as inputs pandas DataFrames with columns ['unique_id', 'ds', 'y'], where unique_id identifies individual time series from the dataset, ds is the date, and y is the target binary variable. In this motivation example we convert 8x8 digits images into 64-length sequences and define a classification problem, to identify when the pixels surpass certain threshold. We declare a pandas dataframe in long format, to match NeuralForecast’s inputs. 
digits = datasets.load_digits()
images = digits.images[:100]

plt.imshow(images[0,:,:], cmap=plt.cm.gray, 
           vmax=16, interpolation="nearest")

pixels = np.reshape(images, (len(images), 64))
ytarget = (pixels > 10) * 1

fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.plot(pixels[10])
ax2.plot(ytarget[10], color='purple')
ax1.set_xlabel('Pixel index')
ax1.set_ylabel('Pixel value')
ax2.set_ylabel('Pixel threshold', color='purple')
plt.grid()
plt.show()

# We flat the images and create an input dataframe
# with 'unique_id' series identifier and 'ds' time stamp identifier.
Y_df = pd.DataFrame.from_dict({
            'unique_id': np.repeat(np.arange(100), 64),
            'ds': np.tile(np.arange(64)+1910, 100),
            'y': ytarget.flatten(), 'pixels': pixels.flatten()})
Y_df
unique_iddsypixels
00191000.0
10191100.0
20191205.0
301913113.0
40191409.0
……………
6395991969114.0
6396991970116.0
639799197103.0
639899197200.0
639999197300.0

​
3. Fit and predict temporal classifiers

​
Fit the models

Using the NeuralForecast.fit method you can train a set of models to your dataset. You can define the forecasting horizon (12 in this example), and modify the hyperparameters of the model. For example, for the NHITS we changed the default hidden size for both encoder and decoders. See the NHITS and MLP model documentation.
Warning For the moment Recurrent-based model family is not available to operate with Bernoulli distribution output. This affects the following methods LSTM, GRU, DilatedRNN, and TCN. This feature is work in progress. 
# %%capture
horizon = 12

# Try different hyperparmeters to improve accuracy.
models = [MLP(h=horizon,                           # Forecast horizon
              input_size=2 * horizon,              # Length of input sequence
              loss=DistributionLoss('Bernoulli'),  # Binary classification loss
              valid_loss=Accuracy(),               # Accuracy validation signal
              max_steps=500,                       # Number of steps to train
              scaler_type='standard',              # Type of scaler to normalize data
              hidden_size=64,                      # Defines the size of the hidden state of the LSTM
              #early_stop_patience_steps=2,         # Early stopping regularization patience
              val_check_steps=10,                  # Frequency of validation signal (affects early stopping)
              ),
          NHITS(h=horizon,                          # Forecast horizon
                input_size=2 * horizon,             # Length of input sequence
                loss=DistributionLoss('Bernoulli'), # Binary classification loss
                valid_loss=Accuracy(),              # Accuracy validation signal                
                max_steps=500,                      # Number of steps to train
                n_freq_downsample=[2, 1, 1],        # Downsampling factors for each stack output
                #early_stop_patience_steps=2,        # Early stopping regularization patience
                val_check_steps=10,                 # Frequency of validation signal (affects early stopping)
                interpolation_mode="nearest",
                )             
          ]
nf = NeuralForecast(models=models, freq=1)
Y_hat_df = nf.cross_validation(df=Y_df, n_windows=1)

# By default NeuralForecast produces forecast intervals
# In this case the lo-x and high-x levels represent the 
# low and high bounds of the prediction accumulating x% probability
Y_hat_df
unique_iddscutoffMLPMLP-medianMLP-lo-90MLP-lo-80MLP-hi-80MLP-hi-90NHITSNHITS-medianNHITS-lo-90NHITS-lo-80NHITS-hi-80NHITS-hi-90y
00196219610.1730.00.00.01.01.00.7611.00.00.01.01.00
10196319610.7841.00.00.01.01.00.5711.00.00.01.01.01
20196419610.0420.00.00.00.00.00.0090.00.00.00.00.00
30196519610.0720.00.00.00.01.00.0540.00.00.00.01.00
40196619610.0590.00.00.00.01.00.0000.00.00.00.00.00
……………………………………………
119599196919610.5511.00.00.01.01.00.6971.00.00.01.01.01
119699197019610.6621.00.00.01.01.00.4650.00.00.01.01.01
119799197119610.3690.00.00.01.01.00.3820.00.00.01.01.00
119899197219610.0560.00.00.00.01.00.0000.00.00.00.00.00
119999197319610.0000.00.00.00.00.00.0000.00.00.00.00.00
# Define classification threshold for final predictions
# If (prob > threshold) -> 1
Y_hat_df['NHITS'] = (Y_hat_df['NHITS'] > 0.5) * 1
Y_hat_df['MLP'] = (Y_hat_df['MLP'] > 0.5) * 1
Y_hat_df
unique_iddscutoffMLPMLP-medianMLP-lo-90MLP-lo-80MLP-hi-80MLP-hi-90NHITSNHITS-medianNHITS-lo-90NHITS-lo-80NHITS-hi-80NHITS-hi-90y
001962196100.00.00.01.01.011.00.00.01.01.00
101963196111.00.00.01.01.011.00.00.01.01.01
201964196100.00.00.00.00.000.00.00.00.00.00
301965196100.00.00.00.01.000.00.00.00.01.00
401966196100.00.00.00.01.000.00.00.00.00.00
……………………………………………
1195991969196111.00.00.01.01.011.00.00.01.01.01
1196991970196111.00.00.01.01.000.00.00.01.01.01
1197991971196100.00.00.01.01.000.00.00.01.01.00
1198991972196100.00.00.00.01.000.00.00.00.00.00
1199991973196100.00.00.00.00.000.00.00.00.00.00

​
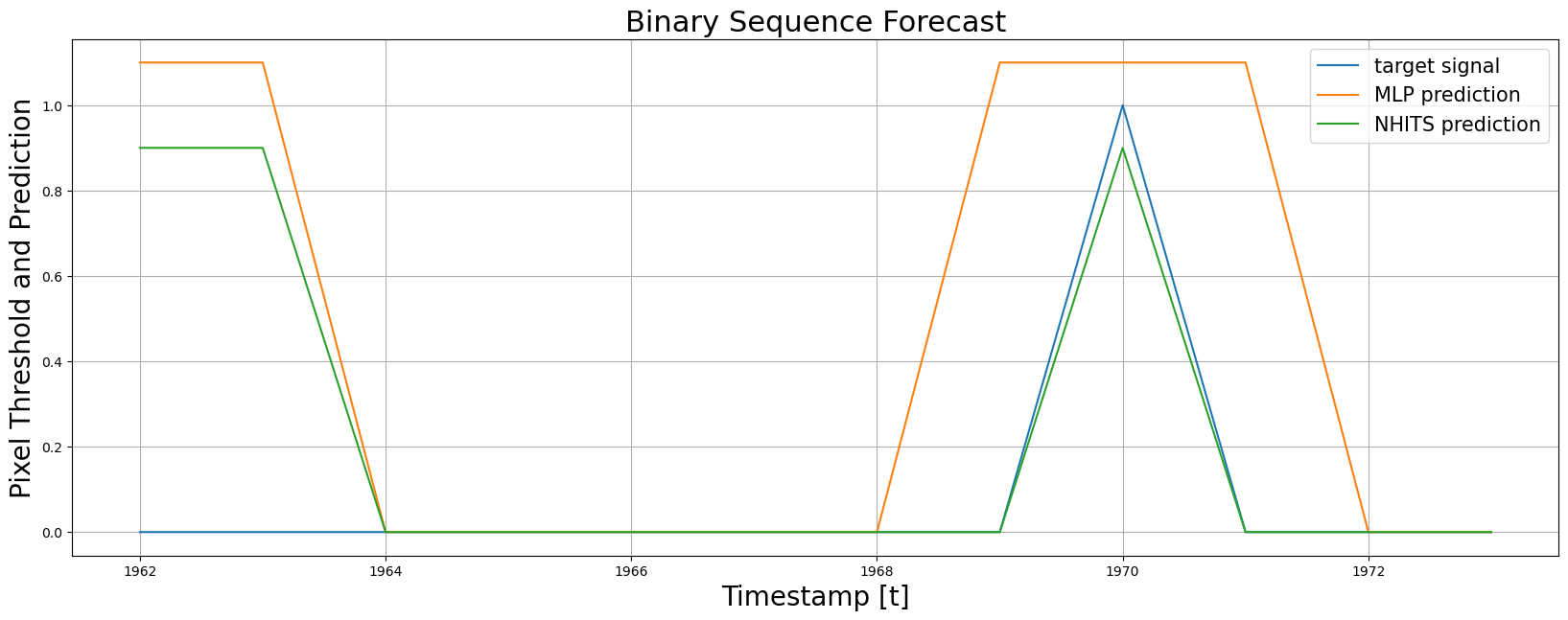
4. Plot and Evaluate Predictions

Finally, we plot the forecasts of both models againts the real values. And evaluate the accuracy of the MLP and NHITS temporal classifiers. 
plot_df = Y_hat_df[Y_hat_df.unique_id==10]

fig, ax = plt.subplots(1, 1, figsize = (20, 7))
plt.plot(plot_df.ds, plot_df.y, label='target signal')
plt.plot(plot_df.ds, plot_df['MLP'] * 1.1, label='MLP prediction')
plt.plot(plot_df.ds, plot_df['NHITS'] * .9, label='NHITS prediction')
ax.set_title('Binary Sequence Forecast', fontsize=22)
ax.set_ylabel('Pixel Threshold and Prediction', fontsize=20)
ax.set_xlabel('Timestamp [t]', fontsize=20)
ax.legend(prop={'size': 15})
ax.grid()

def accuracy(y, y_hat):
    return np.mean(y==y_hat)

mlp_acc = accuracy(y=Y_hat_df['y'], y_hat=Y_hat_df['MLP'])
nhits_acc = accuracy(y=Y_hat_df['y'], y_hat=Y_hat_df['NHITS'])

print(f'MLP Accuracy: {mlp_acc:.1%}')
print(f'NHITS Accuracy: {nhits_acc:.1%}')

MLP Accuracy: 77.8%
NHITS Accuracy: 74.5%

​
References