Time series signal decomposition involves breaking down an original time series into its constituent components. By decomposing the time series, we can gain insights into underlying patterns, trends-cycles, and seasonal effects, enabling improved understanding and forecasting accuracy.

This notebook will show how to use the NHITS/NBEATSx to extract these series’ components. We will:
- Installing NeuralForecast.
- Simulate a Harmonic Signal.
- NHITS’ forecast decomposition.
- NBEATSx’ forecast decomposition.

You can run these experiments using GPU with Google Colab.

​
1. Installing NeuralForecast

!pip install neuralforecast

​
2. Simulate a Harmonic Signal

In this example, we will consider a Harmonic signal comprising two frequencies: one low-frequency and one high-frequency.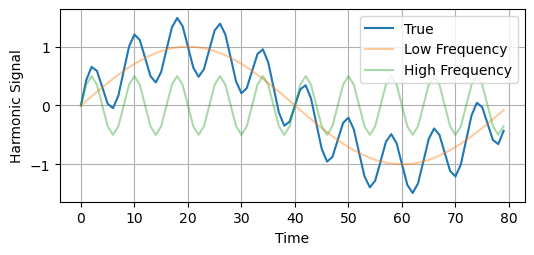

import numpy as np
import pandas as pd

N = 10_000
T = 1.0 / 800.0 # sample spacing
x = np.linspace(0.0, N*T, N, endpoint=False)

y1 = np.sin(10.0 * 2.0*np.pi*x) 
y2 = 0.5 * np.sin(100 * 2.0*np.pi*x)
y = y1 + y2

import matplotlib.pyplot as plt
plt.rcParams["axes.grid"]=True

fig, ax = plt.subplots(figsize=(6, 2.5))
plt.plot(y[-80:], label='True')
plt.plot(y1[-80:], label='Low Frequency', alpha=0.4)
plt.plot(y2[-80:], label='High Frequency', alpha=0.4)
plt.ylabel('Harmonic Signal')
plt.xlabel('Time')
plt.legend()
plt.show()
plt.close()


# Split dataset into train/test
# Last horizon observations for test
horizon = 96
Y_df = pd.DataFrame(dict(unique_id=1, ds=np.arange(len(x)), y=y))
Y_train_df = Y_df.groupby('unique_id').head(len(Y_df)-horizon).reset_index()
Y_test_df = Y_df.groupby('unique_id').tail(horizon).reset_index()
Y_test_df
indexunique_iddsy
0990419904-0.951057
1990519905-0.570326
2990619906-0.391007
3990719907-0.499087
4990819908-0.809017
……………
91999519995-0.029130
92999619996-0.309017
93999719997-0.586999
94999819998-0.656434
95999919999-0.432012

​
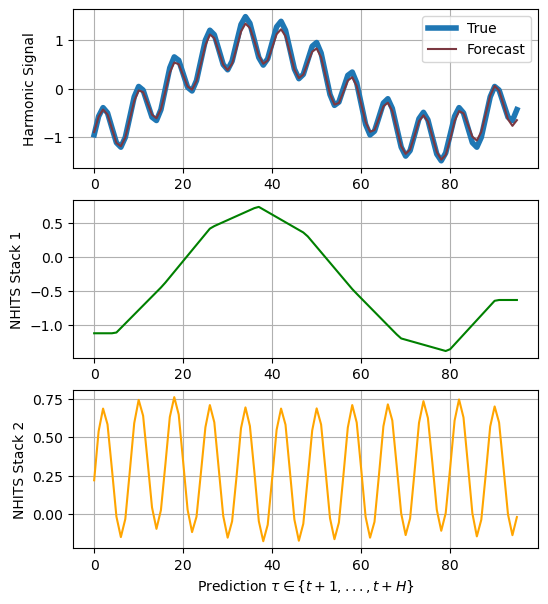
3. NHITS decomposition

We will employ NHITS stack-specialization to recover the latent harmonic functions.

NHITS, a Wavelet-inspired algorithm, allows for breaking down a time series into various scales or resolutions, aiding in the identification of localized patterns or features. The expressivity ratios for each layer enable control over the model’s stack specialization.

from neuralforecast.models import NHITS, NBEATSx
from neuralforecast import NeuralForecast
from neuralforecast.losses.pytorch import HuberLoss, MQLoss

models = [NHITS(h=horizon,                           # Forecast horizon
                input_size=2 * horizon,              # Length of input sequence
                loss=HuberLoss(),                    # Robust Huber Loss
                max_steps=1000,                      # Number of steps to train
                dropout_prob_theta=0.5,
                interpolation_mode='linear',
                stack_types=['identity']*2,
                n_blocks=[1, 1],
                mlp_units=[[64, 64],[64, 64]],
                n_freq_downsample=[10, 1],           # Inverse expressivity ratios for NHITS' stacks specialization
                val_check_steps=10,                  # Frequency of validation signal (affects early stopping)
              )
          ]
nf = NeuralForecast(models=models, freq='M')
nf.fit(df=Y_train_df)

Global seed set to 1

from neuralforecast.tsdataset import TimeSeriesDataset

# NHITS decomposition plot
model = nf.models[0]
dataset, *_ = TimeSeriesDataset.from_df(df = Y_train_df)
y_hat = model.decompose(dataset=dataset)

Predicting DataLoader 0: 100%|██████████| 1/1 [00:00<00:00, 20.68it/s]

fig, ax = plt.subplots(3, 1, figsize=(6, 7))

ax[0].plot(Y_test_df['y'].values, label='True', linewidth=4)
ax[0].plot(y_hat.sum(axis=1).flatten(), label='Forecast', color="#7B3841")
ax[0].legend()
ax[0].set_ylabel('Harmonic Signal')

ax[1].plot(y_hat[0,1]+y_hat[0,0], label='stack1', color="green")
ax[1].set_ylabel('NHITS Stack 1')

ax[2].plot(y_hat[0,2], label='stack2', color="orange")
ax[2].set_ylabel('NHITS Stack 2')
ax[2].set_xlabel(r'Prediction $\tau \in \{t+1,..., t+H\}$')
plt.show()

​
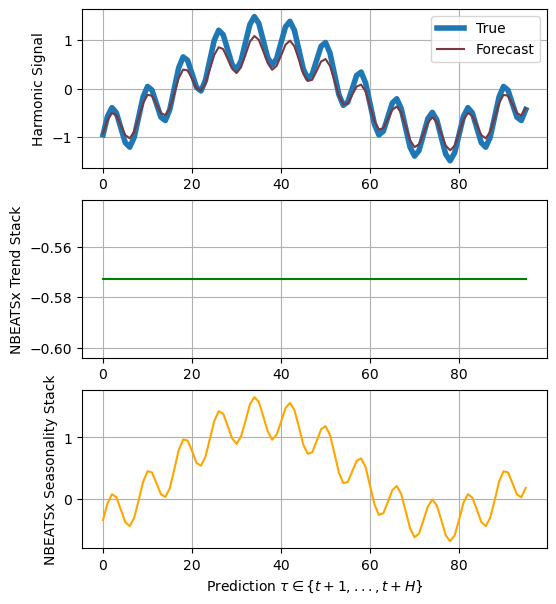
4. NBEATSx decomposition

Here we will employ NBEATSx interpretable basis projection to recover the latent harmonic functions.

NBEATSx, this network in its interpretable variant sequentially projects the signal into polynomials and harmonic basis to learn trend TT and seasonality SS components: y^[t+1:t+H]=θ1T+θ2S\hat{y}_{[t+1:t+H]} = \theta_{1} T + \theta_{2} S

In contrast to NHITS’ wavelet-like projections the basis heavily determine the behavior of the projections. And the Fourier projections are not capable of being immediately decomposed into individual frequencies.

models = [NBEATSx(h=horizon,                           # Forecast horizon
                  input_size=2 * horizon,              # Length of input sequence
                  loss=HuberLoss(),                    # Robust Huber Loss
                  max_steps=1000,                      # Number of steps to train
                  dropout_prob_theta=0.5,
                  stack_types=['trend', 'seasonality'], # Harmonic/Trend projection basis
                  n_polynomials=0,                      # Lower frequencies can be captured by polynomials
                  n_blocks=[1, 1],
                  mlp_units=[[64, 64],[64, 64]],
                  val_check_steps=10,                  # Frequency of validation signal (affects early stopping)
              )
          ]
nf = NeuralForecast(models=models, freq='M')
nf.fit(df=Y_train_df)

Global seed set to 1

# NBEATSx decomposition plot
model = nf.models[0]
dataset, *_ = TimeSeriesDataset.from_df(df = Y_train_df)
y_hat = model.decompose(dataset=dataset)

Predicting DataLoader 0: 100%|██████████| 1/1 [00:00<00:00, 112.51it/s]

fig, ax = plt.subplots(3, 1, figsize=(6, 7))

ax[0].plot(Y_test_df['y'].values, label='True', linewidth=4)
ax[0].plot(y_hat.sum(axis=1).flatten(), label='Forecast', color="#7B3841")
ax[0].legend()
ax[0].set_ylabel('Harmonic Signal')

ax[1].plot(y_hat[0,1]+y_hat[0,0], label='stack1', color="green")
ax[1].set_ylabel('NBEATSx Trend Stack')

ax[2].plot(y_hat[0,2], label='stack2', color="orange")
ax[2].set_ylabel('NBEATSx Seasonality Stack')
ax[2].set_xlabel(r'Prediction $\tau \in \{t+1,..., t+H\}$')
plt.show()

​
References

Robust ForecastingStatistical, Machine Learning and Neural Forecasting methods