In multivariate forecasting, we use the information from every time series to produce all forecasts for all time series jointly. In contrast, in univariate forecasting we only consider the information from every individual time series and produce forecasts for every time series separately. Multivariate forecasting methods thus use more information to produce every forecast, and thus should be able to provide better forecasting results. However, multivariate forecasting methods also scale with the number of time series, which means these methods are commonly less well suited for large-scale problems (i.e. forecasting many, many time series).

In this notebook, we will demonstrate the performance of a state-of-the-art multivariate forecasting architecture TSMixer / TSMixerx when compared to a univariate forecasting method (NHITS) and a simple MLP-based multivariate method (MLPMultivariate).

We will show how to: * Load the ETTm2 benchmark dataset, used in the academic literature. * Train a TSMixer, TSMixerx and MLPMultivariate model * Forecast the test set * Optimize the hyperparameters

You can run these experiments using GPU with Google Colab.

​
1. Installing libraries

!pip install neuralforecast datasetsforecast

​
2. Load ETTm2 Data

The LongHorizon class will automatically download the complete ETTm2 dataset and process it.

It return three Dataframes: Y_df contains the values for the target variables, X_df contains exogenous calendar features and S_df contains static features for each time-series (none for ETTm2). For this example we will use Y_df and X_df.

In TSMixerx, we can make use of the additional exogenous features contained in X_df. In TSMixer, there is no support for exogenous features. Hence, if you want to use exogenous features, you should use TSMixerx.

If you want to use your own data just replace Y_df and X_df. Be sure to use a long format and make sure to have a similar structure as our data set.

import pandas as pd

from datasetsforecast.long_horizon import LongHorizon

# Change this to your own data to try the model
Y_df, X_df, _ = LongHorizon.load(directory='./', group='ETTm2')
Y_df['ds'] = pd.to_datetime(Y_df['ds'])

# X_df contains the exogenous features, which we add to Y_df
X_df['ds'] = pd.to_datetime(X_df['ds'])
Y_df = Y_df.merge(X_df, on=['unique_id', 'ds'], how='left')

# We make validation and test splits
n_time = len(Y_df.ds.unique())
val_size = int(.2 * n_time)
test_size = int(.2 * n_time)

Y_df
unique_iddsyex_1ex_2ex_3ex_4
0HUFL2016-07-01 00:00:00-0.041413-0.5000000.166667-0.500000-0.001370
1HUFL2016-07-01 00:15:00-0.185467-0.5000000.166667-0.500000-0.001370
2HUFL2016-07-01 00:30:00-0.257495-0.5000000.166667-0.500000-0.001370
3HUFL2016-07-01 00:45:00-0.577510-0.5000000.166667-0.500000-0.001370
4HUFL2016-07-01 01:00:00-0.385501-0.4565220.166667-0.500000-0.001370
……………………
403195OT2018-02-20 22:45:00-1.5813250.456522-0.3333330.133333-0.363014
403196OT2018-02-20 23:00:00-1.5813250.500000-0.3333330.133333-0.363014
403197OT2018-02-20 23:15:00-1.5813250.500000-0.3333330.133333-0.363014
403198OT2018-02-20 23:30:00-1.5623280.500000-0.3333330.133333-0.363014
403199OT2018-02-20 23:45:00-1.5623280.500000-0.3333330.133333-0.363014

​
3. Train models

We will train models using the cross_validation method, which allows users to automatically simulate multiple historic forecasts (in the test set).

The cross_validation method will use the validation set for hyperparameter selection and early stopping, and will then produce the forecasts for the test set.

First, instantiate each model in the models list, specifying the horizon, input_size, and training iterations. In this notebook, we compare against the univariate NHITS and multivariate MLPMultivariate models.

# %%capture
from neuralforecast.core import NeuralForecast
from neuralforecast.models import TSMixer, TSMixerx, NHITS, MLPMultivariate
from neuralforecast.losses.pytorch import MSE, MAE

horizon = 96
input_size = 512
models = [
          TSMixer(h=horizon,
                input_size=input_size,
                n_series=7,
                max_steps=1000,
                val_check_steps=100,
                early_stop_patience_steps=5,
                scaler_type='identity',
                valid_loss=MAE(),
                random_seed=12345678,
                ),  
          TSMixerx(h=horizon,
                input_size=input_size,
                n_series=7,
                max_steps=1000,
                val_check_steps=100,
                early_stop_patience_steps=5,
                scaler_type='identity',
                dropout=0.7,
                valid_loss=MAE(),
                random_seed=12345678,
                futr_exog_list=['ex_1', 'ex_2', 'ex_3', 'ex_4'],
                ),
          MLPMultivariate(h=horizon,
                input_size=input_size,
                n_series=7,
                max_steps=1000,
                val_check_steps=100,
                early_stop_patience_steps=5,
                scaler_type='standard',
                hidden_size=256,
                valid_loss=MAE(),
                random_seed=12345678,
                ),                                             
           NHITS(h=horizon,
                input_size=horizon,
                max_steps=1000,
                val_check_steps=100,
                early_stop_patience_steps=5,
                scaler_type='robust',
                valid_loss=MAE(),
                random_seed=12345678,
                ),                                                                       
         ]

INFO:lightning_fabric.utilities.seed:Seed set to 12345678
INFO:lightning_fabric.utilities.seed:Seed set to 12345678
INFO:lightning_fabric.utilities.seed:Seed set to 12345678
INFO:lightning_fabric.utilities.seed:Seed set to 12345678

Tip

Check our auto models for automatic hyperparameter optimization, and see the end of this tutorial for an example of hyperparameter tuning.

Instantiate a NeuralForecast object with the following required parameters:

Second, use the cross_validation method, specifying the dataset (Y_df), validation size and test size.

nf = NeuralForecast(
    models=models,
    freq='15min')

Y_hat_df = nf.cross_validation(df=Y_df,
                               val_size=val_size,
                               test_size=test_size,
                               n_windows=None
                               )                                 
Y_hat_df = Y_hat_df.reset_index()

The cross_validation method will return the forecasts for each model on the test set.

​
4. Evaluate Results

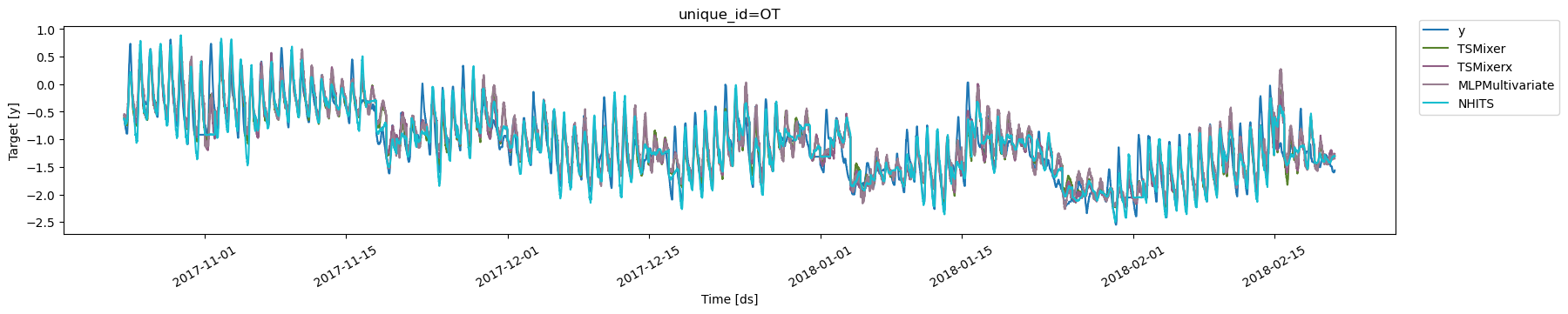
Next, we plot the forecasts on the test set for the OT variable for all models.

import matplotlib.pyplot as plt
Y_plot = Y_hat_df[Y_hat_df['unique_id']=='OT'] # OT dataset
cutoffs = Y_hat_df['cutoff'].unique()[::horizon]
Y_plot = Y_plot[Y_hat_df['cutoff'].isin(cutoffs)]

plt.figure(figsize=(20,5))
plt.plot(Y_plot['ds'], Y_plot['y'], label='True')
for model in models:
    plt.plot(Y_plot['ds'], Y_plot[f'{model}'], label=f'{model}')
plt.xlabel('Datestamp')
plt.ylabel('OT')
plt.grid()
plt.legend()

Finally, we compute the test errors using the Mean Absolute Error (MAE) and Mean Squared Error (MSE):

MAE=1Windows∗Horizon∑τ∣yτ−y^τ∣\qquad MAE = \frac{1}{Windows * Horizon} \sum_{\tau} |y_{\tau} - \hat{y}_{\tau}| \qquad and MSE=1Windows∗Horizon∑τ(yτ−y^τ)2\qquad MSE = \frac{1}{Windows * Horizon} \sum_{\tau} (y_{\tau} - \hat{y}_{\tau})^{2} \qquad

from neuralforecast.losses.numpy import mse, mae

for model in models:
    mae_model = mae(Y_hat_df['y'], Y_hat_df[f'{model}'])
    mse_model = mse(Y_hat_df['y'], Y_hat_df[f'{model}'])
    print(f'{model} horizon {horizon} - MAE: {mae_model:.3f}')
    print(f'{model} horizon {horizon} - MSE: {mse_model:.3f}')

TSMixer horizon 96 - MAE: 0.250
TSMixer horizon 96 - MSE: 0.163
TSMixerx horizon 96 - MAE: 0.257
TSMixerx horizon 96 - MSE: 0.170
MLPMultivariate horizon 96 - MAE: 0.322
MLPMultivariate horizon 96 - MSE: 0.257
NHITS horizon 96 - MAE: 0.251
NHITS horizon 96 - MSE: 0.179

For reference, we can check the performance when compared to self-reported performance in the paper. We find that TSMixer provides better results than the univariate method NHITS. Also, our implementation of TSMixer very closely tracks the results of the original paper. Finally, it seems that there is little benefit of using the additional exogenous variables contained in the dataframe X_df as TSMixerx performs worse than TSMixer, especially on longer horizons. Note also that MLPMultivariate clearly underperforms as compared to the other methods, which can be somewhat expected given its relative simplicity.

Mean Absolute Error (MAE)

HorizonTSMixer
(this notebook)		TSMixer
(paper)		TSMixerx
(this notebook)		NHITS
(this notebook)		NHITS
(paper)		MLPMultivariate
(this notebook)
960.2500.2520.2570.2510.2550.322
1920.2880.2900.3000.2910.3050.361
3360.3230.3240.3800.3440.3460.390
7200.3770.4220.4640.4170.4130.608

Mean Squared Error (MSE)

HorizonTSMixer
(this notebook)		TSMixer
(paper)		TSMixerx
(this notebook)		NHITS
(this notebook)		NHITS
(paper)		MLPMultivariate
(this notebook)
960.1630.1630.1700.1790.1760.255
1920.2200.2160.2310.2390.2450.330
3360.2720.2680.3610.3110.2950.376
7200.3560.4200.4930.4510.4013.421

Note that for the table above, we use the same hyperparameters for all methods for all horizons, whereas the original papers tune the hyperparameters for each horizon.

​
5. Tuning the hyperparameters

The AutoTSMixer / AutoTSMixerx class will automatically perform hyperparamter tunning using the Tune library, exploring a user-defined or default search space. Models are selected based on the error on a validation set and the best model is then stored and used during inference.

The AutoTSMixer.default_config / AutoTSMixerx.default_config attribute contains a suggested hyperparameter space. Here, we specify a different search space following the paper’s hyperparameters. Feel free to play around with this space.

For this example, we will optimize the hyperparameters for horizon = 96.

from ray import tune
from ray.tune.search.hyperopt import HyperOptSearch
from neuralforecast.auto import AutoTSMixer, AutoTSMixerx

horizon = 96 # 24hrs = 4 * 15 min.

tsmixer_config = {
       "input_size": input_size,                                                 # Size of input window
       "max_steps": tune.choice([500, 1000, 2000]),                              # Number of training iterations
       "val_check_steps": 100,                                                   # Compute validation every x steps
       "early_stop_patience_steps": 5,                                           # Early stopping steps
       "learning_rate": tune.loguniform(1e-4, 1e-2),                             # Initial Learning rate
       "n_block": tune.choice([1, 2, 4, 6, 8]),                                  # Number of mixing layers
       "dropout": tune.uniform(0.0, 0.99),                                       # Dropout
       "ff_dim": tune.choice([32, 64, 128]),                                     # Dimension of the feature linear layer
       "scaler_type": 'identity',       
    }

tsmixerx_config = tsmixer_config.copy()
tsmixerx_config['futr_exog_list'] = ['ex_1', 'ex_2', 'ex_3', 'ex_4']

To instantiate AutoTSMixer and AutoTSMixerx you need to define:

  • h: forecasting horizon
  • n_series: number of time series in the multivariate time series problem.

In addition, we define the following parameters (if these are not given, the AutoTSMixer/AutoTSMixerx class will use a pre-defined value): * loss: training loss. Use the DistributionLoss to produce probabilistic forecasts. * config: hyperparameter search space. If None, the AutoTSMixer class will use a pre-defined suggested hyperparameter space. * num_samples: number of configurations explored. For this example, we only use a limited amount of 10. * search_alg: type of search algorithm used for selecting parameter values within the hyperparameter space. * backend: the backend used for the hyperparameter optimization search, either ray or optuna. * valid_loss: the loss used for the validation sets in the optimization procedure.

model = AutoTSMixer(h=horizon,
                    n_series=7,
                    loss=MAE(),
                    config=tsmixer_config,
                    num_samples=10,
                    search_alg=HyperOptSearch(),
                    backend='ray',
                    valid_loss=MAE())

modelx = AutoTSMixerx(h=horizon,
                    n_series=7,
                    loss=MAE(),
                    config=tsmixerx_config,
                    num_samples=10,
                    search_alg=HyperOptSearch(),
                    backend='ray',
                    valid_loss=MAE())

Now, we fit the model by instantiating a NeuralForecast object with the following required parameters:

The cross_validation method allows you to simulate multiple historic forecasts, greatly simplifying pipelines by replacing for loops with fit and predict methods.

With time series data, cross validation is done by defining a sliding window across the historical data and predicting the period following it. This form of cross validation allows us to arrive at a better estimation of our model’s predictive abilities across a wider range of temporal instances while also keeping the data in the training set contiguous as is required by our models.

The cross_validation method will use the validation set for hyperparameter selection, and will then produce the forecasts for the test set.

nf = NeuralForecast(models=[model, modelx], freq='15min')
Y_hat_df = nf.cross_validation(df=Y_df, val_size=val_size,
                               test_size=test_size, n_windows=None)

2024-03-22 09:08:28,183 INFO worker.py:1724 -- Started a local Ray instance.
2024-03-22 09:08:29,427 INFO tune.py:220 -- Initializing Ray automatically. For cluster usage or custom Ray initialization, call `ray.init(...)` before `Tuner(...)`.
2024-03-22 09:08:29,429 INFO tune.py:583 -- [output] This uses the legacy output and progress reporter, as Jupyter notebooks are not supported by the new engine, yet. For more information, please see https://github.com/ray-project/ray/issues/36949
2024-03-22 09:08:45,570 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:09:03,688 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:09:17,107 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:09:28,650 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:09:47,489 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:10:19,949 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:11:20,191 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:11:30,224 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:12:06,451 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:12:28,275 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
INFO:lightning_fabric.utilities.seed:Seed set to 1
2024-03-22 09:13:12,831 INFO tune.py:583 -- [output] This uses the legacy output and progress reporter, as Jupyter notebooks are not supported by the new engine, yet. For more information, please see https://github.com/ray-project/ray/issues/36949
2024-03-22 09:13:42,119 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:14:08,067 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:14:34,340 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:14:59,946 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:16:44,930 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:17:02,576 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:17:22,409 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:17:41,035 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:18:02,149 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
2024-03-22 09:19:45,156 INFO tensorboardx.py:275 -- Removed the following hyperparameter values when logging to tensorboard: {'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'), 'loss': ('__ref_ph', 'de895953'), 'valid_loss': ('__ref_ph', '004b9a7a')}
INFO:lightning_fabric.utilities.seed:Seed set to 1

​
6. Evaluate Results

The AutoTSMixer/AutoTSMixerx class contains a results attribute that stores information of each configuration explored. It contains the validation loss and best validation hyperparameter. The result dataframe Y_hat_df that we obtained in the previous step is based on the best config of the hyperparameter search. For AutoTSMixer, the best config is:

nf.models[0].results.get_best_result().config

{'input_size': 512,
 'max_steps': 2000,
 'val_check_steps': 100,
 'early_stop_patience_steps': 5,
 'learning_rate': 0.0008831625975972278,
 'n_block': 1,
 'dropout': 0.531963627534685,
 'ff_dim': 128,
 'scaler_type': 'identity',
 'n_series': 7,
 'h': 96,
 'loss': MAE(),
 'valid_loss': MAE()}

and for AutoTSMixerx:

nf.models[1].results.get_best_result().config

{'input_size': 512,
 'max_steps': 500,
 'val_check_steps': 100,
 'early_stop_patience_steps': 5,
 'learning_rate': 0.006813015000503828,
 'n_block': 1,
 'dropout': 0.6915259307542235,
 'ff_dim': 32,
 'scaler_type': 'identity',
 'futr_exog_list': ('ex_1', 'ex_2', 'ex_3', 'ex_4'),
 'n_series': 7,
 'h': 96,
 'loss': MAE(),
 'valid_loss': MAE()}

We compute the test errors of the best config for the two metrics of interest:

MAE=1Windows∗Horizon∑τ∣yτ−y^τ∣\qquad MAE = \frac{1}{Windows * Horizon} \sum_{\tau} |y_{\tau} - \hat{y}_{\tau}| \qquad and MSE=1Windows∗Horizon∑τ(yτ−y^τ)2\qquad MSE = \frac{1}{Windows * Horizon} \sum_{\tau} (y_{\tau} - \hat{y}_{\tau})^{2} \qquad

y_true = Y_hat_df.y.values
y_hat_tsmixer = Y_hat_df['AutoTSMixer'].values
y_hat_tsmixerx = Y_hat_df['AutoTSMixerx'].values

print(f'MAE TSMixer: {mae(y_hat_tsmixer, y_true):.3f}')
print(f'MSE TSMixer: {mse(y_hat_tsmixer, y_true):.3f}')
print(f'MAE TSMixerx: {mae(y_hat_tsmixerx, y_true):.3f}')
print(f'MSE TSMixerx: {mse(y_hat_tsmixerx, y_true):.3f}')

MAE TSMixer: 0.250
MSE TSMixer: 0.163
MAE TSMixerx: 0.264
MSE TSMixerx: 0.178

We can compare the error metrics for our optimized setting to the earlier setting in which we used the default hyperparameters. In this case, for a horizon of 96, we got slightly improved results for TSMixer on MAE. Interestingly, we did not improve for TSMixerx as compared to the default settings. For this dataset, it seems there is limited value in using exogenous features with the TSMixerx architecture for a horizon of 96.

MetricTSMixer
(optimized)		TSMixer
(default)		TSMixer
(paper)		TSMixerx
(optimized)		TSMixerx
(default)
MAE0.2470.2500.2520.2580.257
MSE0.1620.1630.1630.1740.170

Note that we only evaluated 10 hyperparameter configurations (num_samples=10), which may suggest that it is possible to further improve forecasting performance by exploring more hyperparameter configurations.

​
References

Chen, Si-An, Chun-Liang Li, Nate Yoder, Sercan O. Arik, and Tomas Pfister (2023). “TSMixer: An All-MLP Architecture for Time Series Forecasting.”
Cristian Challu, Kin G. Olivares, Boris N. Oreshkin, Federico Garza, Max Mergenthaler-Canseco, Artur Dubrawski (2021). NHITS: Neural Hierarchical Interpolation for Time Series Forecasting. Accepted at AAAI 2023.

Forecasting with TFT: Temporal Fusion TransformerProbabilistic Forecasting