Time series cross-validation is a method for evaluating how a model would have performed on historical data. It works by defining a sliding window across past observations and predicting the period following it. It differs from standard cross-validation by maintaining the chronological order of the data instead of randomly splitting it. This method allows for a better estimation of our model’s predictive capabilities by considering multiple periods. When only one window is used, it resembles a standard train-test split, where the test data is the last set of observations, and the training set consists of the earlier data. The following graph showcases how time series cross-validation works. 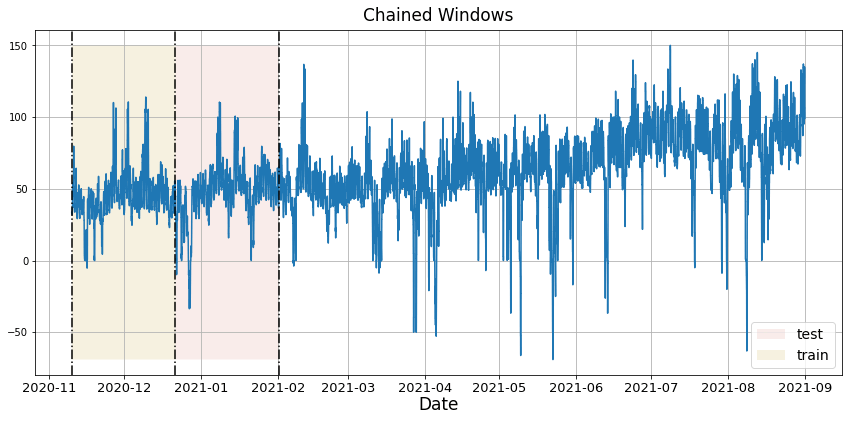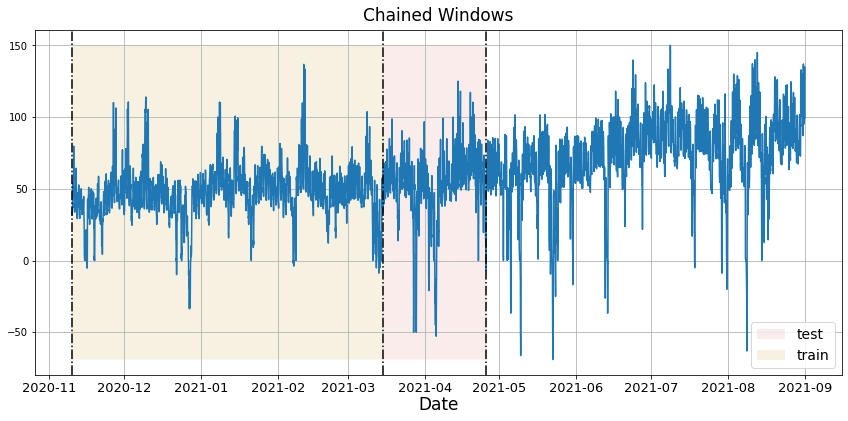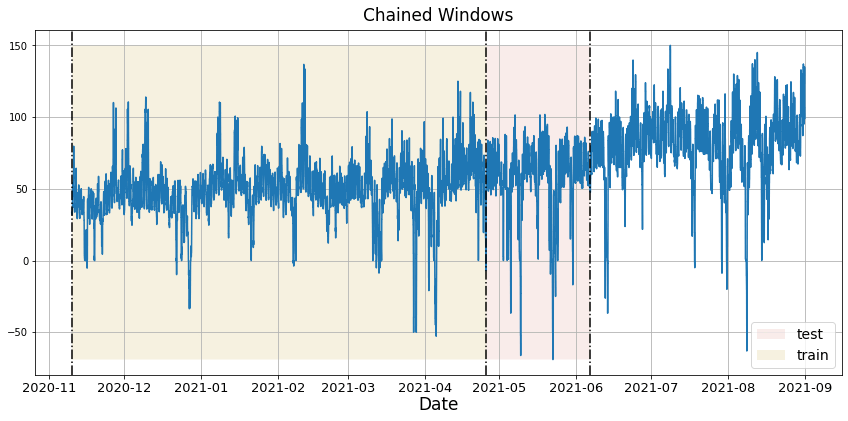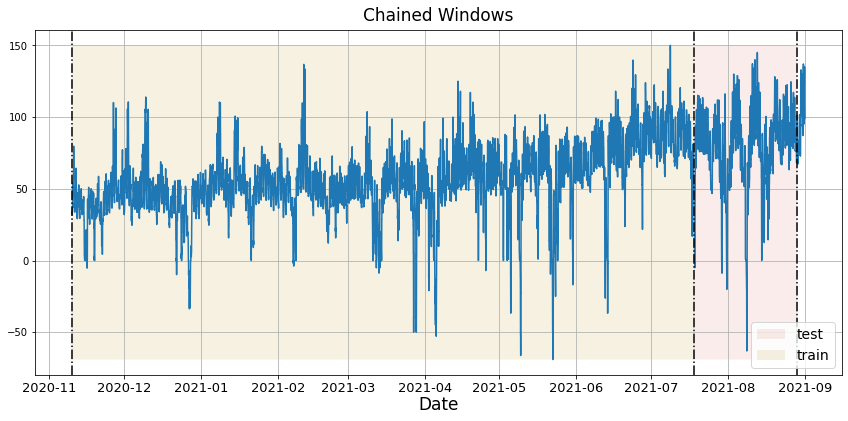In this tutorial we’ll explain how to perform cross-validation in NeuralForecast. Outline: 1. Install NeuralForecast
  1. Load and plot the data
  2. Train multiple models using cross-validation
  3. Evaluate models and select the best for each series
  4. Plot cross-validation results
Prerequesites This guide assumes basic familiarity with neuralforecast. For a minimal example visit the Quick Start

​
1. Install NeuralForecast

!pip install neuralforecast

​
2. Load and plot the data

We’ll use pandas to load the hourly dataset from the M4 Forecasting Competition, which has been stored in a parquet file for efficiency. 
import os
import logging

import pandas as pd
from IPython.display import display

os.environ['PL_TRAINER_ENABLE_PROGRESS_BAR'] = '0'
logging.getLogger('pytorch_lightning').setLevel(logging.ERROR)

Y_df = pd.read_parquet('https://datasets-nixtla.s3.amazonaws.com/m4-hourly.parquet')
Y_df.head()
unique_iddsy
0H11605.0
1H12586.0
2H13586.0
3H14559.0
4H15511.0
The input to neuralforecast should be a data frame in long format with three columns: unique_id, ds, and y.
  • unique_id (string, int, or category): A unique identifier for each time series.
  • ds (int or timestamp): An integer indexing time or a timestamp in format YYYY-MM-DD or YYYY-MM-DD HH:MM:SS.
  • y (numeric): The target variable to forecast.
This dataset contains 414 unique time series. To reduce the total execution time, we’ll use only the first 10. 
uids = Y_df['unique_id'].unique()[:10] # Select 10 ids to make the example run faster
Y_df = Y_df.query('unique_id in @uids').reset_index(drop=True)
To plot the series, we’ll use the plot_series method from utilsforecast.plotting. utilsforecast is a dependency of neuralforecast so it should be already installed. 
from utilsforecast.plotting import plot_series

plot_series(Y_df)

​
3. Train multiple models using cross-validation

We’ll train different models from neuralforecast using the cross-validation method to decide which one perfoms best on the historical data. To do this, we need to import the NeuralForecast class and the models that we want to compare. 
from neuralforecast import NeuralForecast 
from neuralforecast.auto import MLP, NBEATS, NHITS
from neuralforecast.losses.pytorch import MQLoss
In this tutorial, we will use neuralforecast's MPL, NBEATS, and NHITS models. First, we need to create a list of models and then instantiate the NeuralForecast class. For each model, we’ll define the following hyperparameters:
  • h: The forecast horizon. Here, we will use the same horizon as in the M4 competition, which was 48 steps ahead.
  • input_size: The number of historical observations (lags) that the model uses to make predictions. In this case, it will be twice the forecast horizon.
  • loss: The loss function to optimize. Here, we’ll use the Multi Quantile Loss (MQLoss) from neuralforecast.losses.pytorch.
Warning The Multi Quantile Loss (MQLoss) is the sum of the quantile losses for each target quantile. The quantile loss for a single quantile measures how well a model has predicted a specific quantile of the actual distribution, penalizing overestimations and underestimations asymmetrically based on the quantile’s value. For more details see here.
While there are other hyperparameters that can be defined for each model, we’ll use the default values for the purposes of this tutorial. To learn more about the hyperparameters of each model, please check out the corresponding documentation. 
horizon = 48 
models = [MLP(h=horizon, input_size=2*horizon, loss=MQLoss()), 
          NBEATS(h=horizon, input_size=2*horizon, loss=MQLoss()), 
          NHITS(h=horizon, input_size=2*horizon, loss=MQLoss()),]
nf = NeuralForecast(models=models, freq=1)
The cross_validation method takes the following arguments:
  • df: The data frame in the format described in section 2.
  • n_windows (int): The number of windows to evaluate. Default is 1 and here we’ll use 3.
  • step_size (int): The number of steps between consecutive windows to produce the forecasts. In this example, we’ll set step_size=horizon to produce non-overlapping forecasts. The following diagram shows how the forecasts are produced based on the step_size parameter and forecast horizon h of a model. In this diagram step_size=2 and h=4.
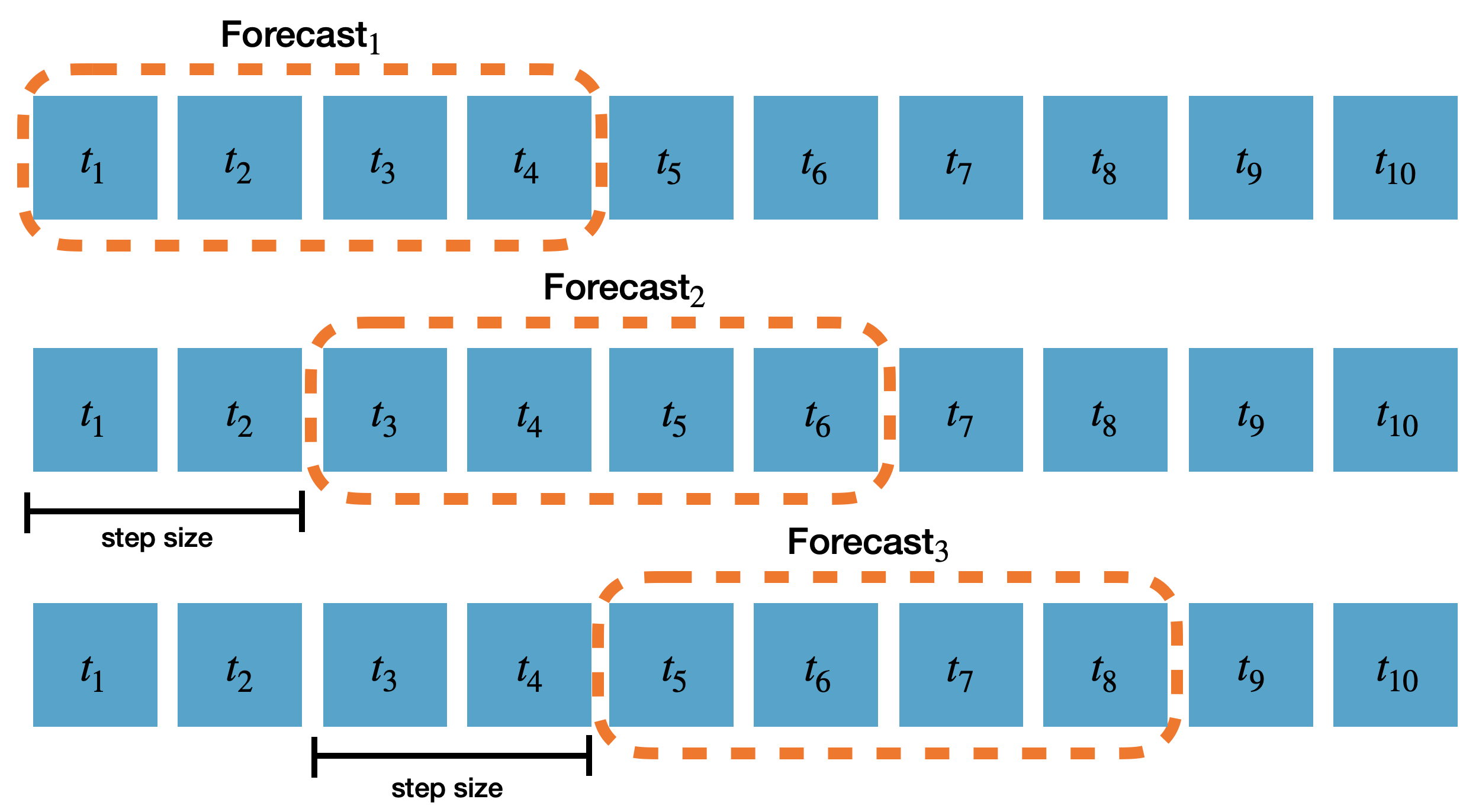
  • refit (bool or int): Whether to retrain models for each cross-validation window. If False, the models are trained at the beginning and then used to predict each window. If a positive integer, the models are retrained every refit windows. Default is False, but here we’ll use refit=1 so that the models are retrained after each window using the data with timestamps up to and including the cutoff.
cv_df = nf.cross_validation(Y_df, n_windows=3, step_size=horizon, refit=1)
It’s worth mentioning that the default version of the cross_validation method in neuralforecast diverges from other libraries, where models are typically retrained at the start of each window. By default, it trains the models once and then uses them to generate predictions over all the windows, thus reducing the total execution time. For scenarios where the models need to be retrained, you can use the refit parameter to specify the number of windows after which the models should be retrained. 
cv_df.head()
unique_iddscutoffMLP-medianMLP-lo-90MLP-lo-80MLP-hi-80MLP-hi-90NBEATS-medianNBEATS-lo-90NBEATS-lo-80NBEATS-hi-80NBEATS-hi-90NHITS-medianNHITS-lo-90NHITS-lo-80NHITS-hi-80NHITS-hi-90y
0H1605604638.964111528.127747546.731812714.415466750.265259623.230896580.549744587.317688647.942505654.148682625.377930556.786926577.746765657.901611670.458069622.0
1H1606604588.216370445.395081483.736542684.394592670.042358552.829407501.618988529.007507593.528564603.152527555.956177511.696350526.399597604.318970622.839722558.0
2H1607604542.242737419.206757439.244476617.775269638.583923495.155548451.871613467.183533550.048950574.697021502.860077462.284668460.950287555.336731571.852722513.0
3H1608604494.055573414.775085427.531647583.965759602.303772465.182556403.593140410.033203500.744019518.277954460.588684406.762390418.040710501.833740515.022095476.0
4H1609604469.330688361.437927378.501373557.875244569.767273441.072388371.541504401.923584483.667877485.047729441.463043393.917725394.483337475.985229499.001373449.0
The output of the cross-validation method is a data frame that includes the following columns:
  • unique_id: The unique identifier for each time series.
  • ds: The timestamp or temporal index.
  • cutoff: The last timestamp or temporal index used in that cross-validation window.
  • "model": Columns with the model’s point forecasts (median) and prediction intervals. By default, the 80 and 90% prediction intervals are included when using the MQLoss.
  • y: The actual value.

​
4. Evaluate models and select the best for each series

To evaluate the point forecasts of the models, we’ll use the Root Mean Squared Error (RMSE), defined as the square root of the mean of the squared differences between the actual and the predicted values. For convenience, we’ll use the evaluate and the rmse functions from utilsforecast. 
from utilsforecast.evaluation import evaluate
from utilsforecast.losses import rmse
The evaluate function takes the following arguments:
  • df: The data frame with the forecasts to evaluate.
  • metrics (list): The metrics to compute.
  • models (list): Names of the models to evaluate. Default is None, which uses all columns after removing id_col, time_col, and target_col.
  • id_col (str): Column that identifies unique ids of the series. Default is unique_id.
  • time_col (str): Column with the timestamps or the temporal index. Default is ds.
  • target_col (str): Column with the target variable. Default is y.
Notice that if we use the default value of models, then we need to exclude the cutoff column from the cross-validation data frame. 
evaluation_df = evaluate(cv_df.drop(columns='cutoff'), metrics=[rmse])
For each unique id, we’ll select the model with the lowest RMSE. 
evaluation_df['best_model'] = evaluation_df.drop(columns=['metric', 'unique_id']).idxmin(axis=1)
evaluation_df
unique_idmetricMLP-medianNBEATS-medianNHITS-medianbest_model
0H1rmse46.65439049.59530447.651201MLP-median
1H10rmse24.19208121.58014216.887989NHITS-median
2H100rmse171.958998178.820952170.452623NHITS-median
3H101rmse331.270162260.021871169.453119NHITS-median
4H102rmse440.470939362.602167326.571391NHITS-median
5H103rmse9069.9376039267.9252578578.535681NHITS-median
6H104rmse189.534415169.017976226.442403NBEATS-median
7H105rmse341.029706284.038751262.140145NHITS-median
8H106rmse203.723728328.128422298.377068MLP-median
9H107rmse212.384943161.445838231.303421NBEATS-median
We can summarize the results to see how many times each model won. 
summary_df = evaluation_df.groupby(['metric', 'best_model']).size().sort_values().to_frame()
summary_df = summary_df.reset_index()
summary_df.columns = ['metric', 'model', 'num. of unique_ids']
summary_df
metricmodelnum. of unique_ids
0rmseMLP-median2
1rmseNBEATS-median2
2rmseNHITS-median6
With this information, we now know which model performs best for each series in the historical data.

​
5. Plot cross-validation results

To visualize the cross-validation results, we will use the plot_series method again. We’ll need to rename the y column in the cross-validation output to avoid duplicates with the original data frame. We’ll also exclude the cutoff column and use the max_insample_length argument to plot only the last 300 observations for better visualization. 
cv_df.rename(columns = {'y': 'actual'}, inplace=True) # rename actual values 
plot_series(Y_df, cv_df.drop(columns='cutoff'), max_insample_length=300)
To clarify the concept of cross-validation further, we’ll plot the forecasts generated at each cutoff for the series with unique_id='H1'. There are three cutoffs because we set n_windows=3. In this example, we used refit=1, so each model is retrained for each window using data with timestamps up to and including the respective cutoff. Additionally, since step_size is equal to the forecast horizon, the resulting forecasts are non-overlapping 
cutoff1, cutoff2, cutoff3 = cv_df['cutoff'].unique()
for cutoff in cv_df['cutoff'].unique():
    display(
        plot_series(
            Y_df,
            cv_df[cv_df['cutoff'] == cutoff].drop(columns='cutoff'),
            ids=['H1'], # use ids parameter to select specific series
        )
    )