The most important train signal is the forecast error, which is the difference between the observed value

y_{\tau}

and the prediction

\hat{y}_{\tau}

, at time

y_{\tau}

e_{\tau} = y_{\tau}-\hat{y}_{\tau} \qquad \qquad \tau \in \{t+1,\dots,t+H \}

The train loss summarizes the forecast errors in different train optimization objectives. All the losses are torch.nn.modules which helps to automatically moved them across CPU/GPU/TPU devices with Pytorch Lightning.

`BasePointLoss`

BasePointLoss(
    horizon_weight=None, outputsize_multiplier=None, output_names=None
)

Bases: Module Base class for point loss functions. Parameters:

Name	Type	Description	Default
`horizon_weight`	`Optional[Tensor]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`
`outputsize_multiplier`	`Optional[int]`	Multiplier for the output size. Defaults to None.	`None`
`output_names`	`Optional[List[str]]`	Names of the outputs. Defaults to None.	`None`

1. Scale-dependent Errors

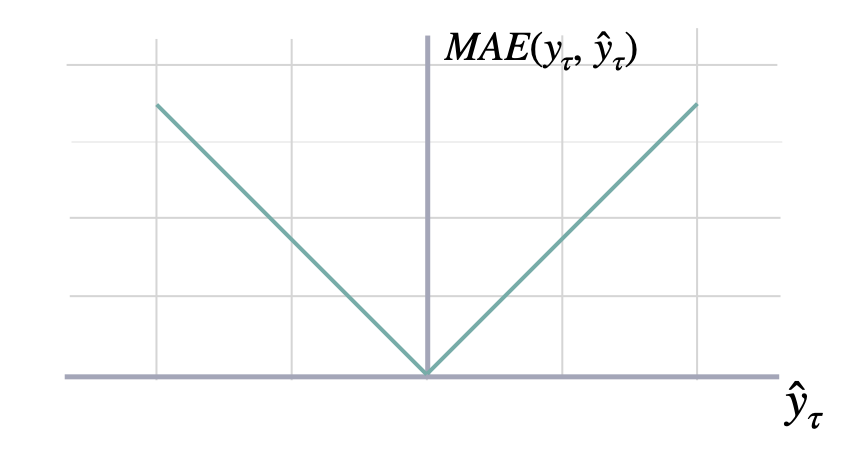
These metrics are on the same scale as the data.

Mean Absolute Error (MAE)

`MAE`

MAE(horizon_weight=None)

Bases: BasePointLoss Mean Absolute Error. Calculates Mean Absolute Error between y and y_hat. MAE measures the relative prediction accuracy of a forecasting method by calculating the deviation of the prediction and the true value at a given time and averages these devations over the length of the series.

\mathrm{MAE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} |y_{\tau} - \hat{y}_{\tau}|

Parameters:

Name	Type	Description	Default
`horizon_weight`	`Optional[Tensor]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`MAE.call`

__call__(y, y_hat, mask=None, y_insample=None)

Calculate Mean Absolute Error between actual and predicted values. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies datapoints to consider in loss. Defaults to None.	`None`
`y_insample`	`Union[Tensor, None]`	Actual insample values. Defaults to None.	`None`

Returns:

Type	Description
`Tensor`	torch.Tensor: MAE (single value).

Mean Squared Error (MSE)

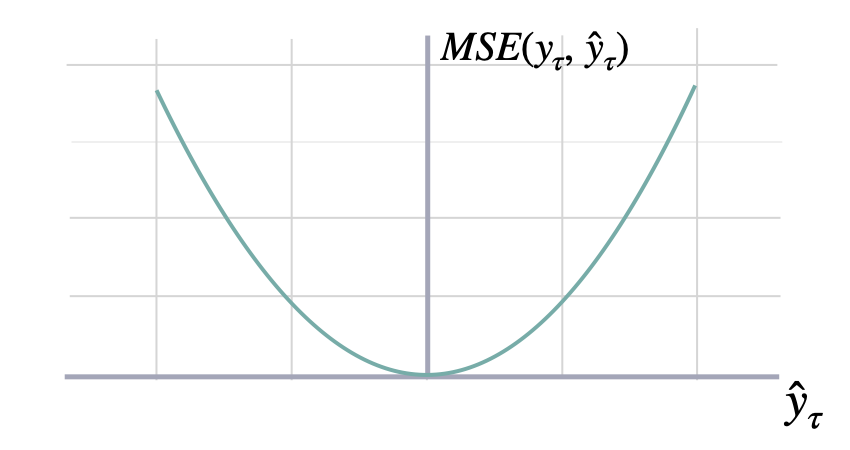
`MSE`

MSE(horizon_weight=None)

Bases: BasePointLoss Mean Squared Error. Calculates Mean Squared Error between y and y_hat. MSE measures the relative prediction accuracy of a forecasting method by calculating the squared deviation of the prediction and the true value at a given time, and averages these devations over the length of the series.

\mathrm{MSE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} (y_{\tau} - \hat{y}_{\tau})^{2}

Parameters:

Name	Type	Description	Default
`horizon_weight`	`Optional[Tensor]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`MSE.call`

__call__(y, y_hat, y_insample=None, mask=None)

Calculate Mean Squared Error between actual and predicted values. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`y_insample`	`Union[Tensor, None]`	Actual insample values. Defaults to None.	`None`
`mask`	`Union[Tensor, None]`	Specifies datapoints to consider in loss. Defaults to None.	`None`

Returns:

Type	Description
`Tensor`	torch.Tensor: MSE (single value).

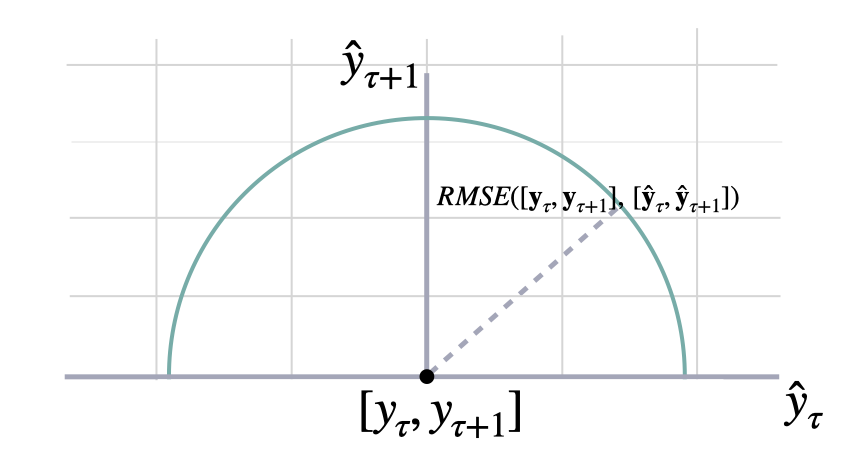
Root Mean Squared Error (RMSE)

`RMSE`

RMSE(horizon_weight=None)

Bases: BasePointLoss Root Mean Squared Error. Calculates Root Mean Squared Error between y and y_hat. RMSE measures the relative prediction accuracy of a forecasting method by calculating the squared deviation of the prediction and the observed value at a given time and averages these devations over the length of the series. Finally the RMSE will be in the same scale as the original time series so its comparison with other series is possible only if they share a common scale. RMSE has a direct connection to the L2 norm.

\mathrm{RMSE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \sqrt{\frac{1}{H} \sum^{t+H}_{\tau=t+1} (y_{\tau} - \hat{y}_{\tau})^{2}}

Parameters:

Name	Type	Description	Default
`horizon_weight`	`Optional[Tensor]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`RMSE.call`

__call__(y, y_hat, mask=None, y_insample=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Tensor, Actual values.	required
`y_hat`	`Tensor`	Tensor, Predicted values.	required
`mask`	`Union[Tensor, None]`	Tensor, Specifies datapoints to consider in loss.	`None`

Returns:

Name	Type	Description
`rmse`	`Tensor`	Tensor (single value).

2. Percentage errors

These metrics are unit-free, suitable for comparisons across series.

Mean Absolute Percentage Error (MAPE)

`MAPE`

MAPE(horizon_weight=None)

Bases: BasePointLoss Mean Absolute Percentage Error Calculates Mean Absolute Percentage Error between y and y_hat. MAPE measures the relative prediction accuracy of a forecasting method by calculating the percentual deviation of the prediction and the observed value at a given time and averages these devations over the length of the series. The closer to zero an observed value is, the higher penalty MAPE loss assigns to the corresponding error.

\mathrm{MAPE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \frac{|y_{\tau}-\hat{y}_{\tau}|}{|y_{\tau}|}

Parameters:

Name	Type	Description	Default
`horizon_weight`		Tensor of size h, weight for each timestamp of the forecasting window.	`None`

`MAPE.call`

__call__(y, y_hat, y_insample=None, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Tensor, Actual values.	required
`y_hat`	`Tensor`	Tensor, Predicted values.	required
`mask`	`Union[Tensor, None]`	Tensor, Specifies date stamps per serie to consider in loss.	`None`

Returns:

Name	Type	Description
`mape`	`Tensor`	Tensor (single value).

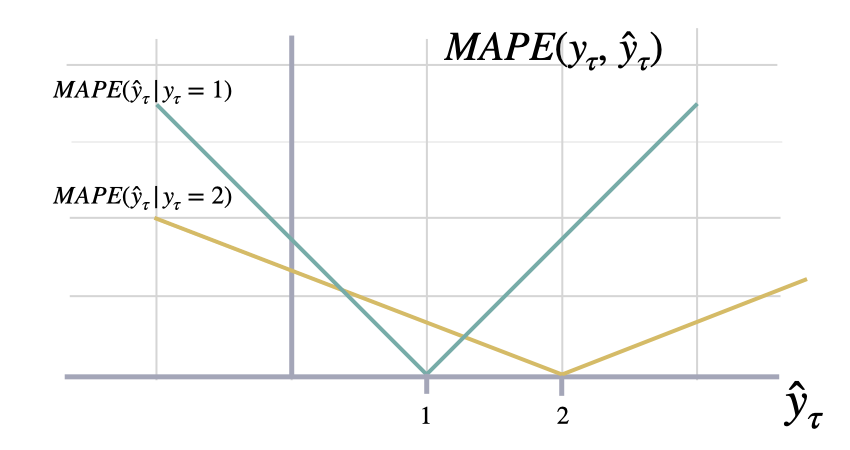
Symmetric MAPE (sMAPE)

`SMAPE`

SMAPE(horizon_weight=None)

Bases: BasePointLoss Symmetric Mean Absolute Percentage Error Calculates Symmetric Mean Absolute Percentage Error between y and y_hat. SMAPE measures the relative prediction accuracy of a forecasting method by calculating the relative deviation of the prediction and the observed value scaled by the sum of the absolute values for the prediction and observed value at a given time, then averages these devations over the length of the series. This allows the SMAPE to have bounds between 0% and 200% which is desireble compared to normal MAPE that may be undetermined when the target is zero.

\mathrm{sMAPE}_{2}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \frac{|y_{\tau}-\hat{y}_{\tau}|}{|y_{\tau}|+|\hat{y}_{\tau}|}

Parameters:

Name	Type	Description	Default
`horizon_weight`		Tensor of size h, weight for each timestamp of the forecasting window.	`None`

`SMAPE.call`

__call__(y, y_hat, mask=None, y_insample=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Tensor, Actual values.	required
`y_hat`	`Tensor`	Tensor, Predicted values.	required
`mask`	`Union[Tensor, None]`	Tensor, Specifies date stamps per serie to consider in loss.	`None`

Returns:

Name	Type	Description
`smape`	`Tensor`	Tensor (single value).

3. Scale-independent Errors

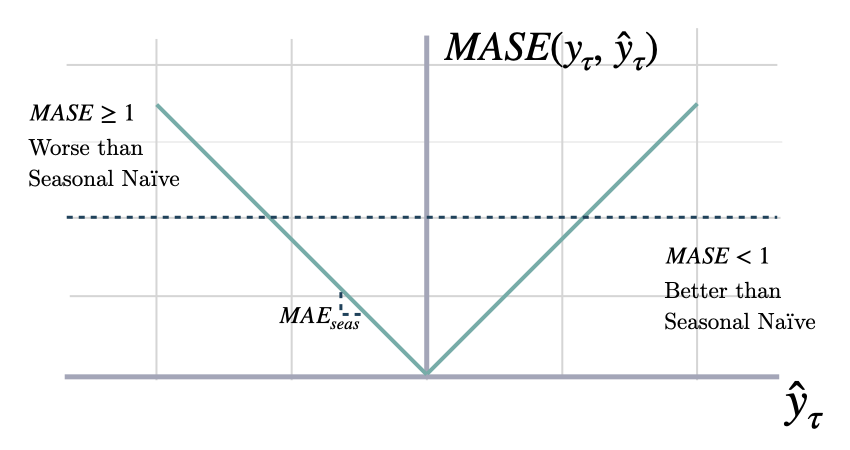
These metrics measure the relative improvements versus baselines.

Mean Absolute Scaled Error (MASE)

`MASE`

MASE(seasonality, horizon_weight=None)

Bases: BasePointLoss Mean Absolute Scaled Error Calculates the Mean Absolute Scaled Error between y and y_hat. MASE measures the relative prediction accuracy of a forecasting method by comparinng the mean absolute errors of the prediction and the observed value against the mean absolute errors of the seasonal naive model. The MASE partially composed the Overall Weighted Average (OWA), used in the M4 Competition.

\mathrm{MASE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}, \mathbf{\hat{y}}^{season}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \frac{|y_{\tau}-\hat{y}_{\tau}|}{\mathrm{MAE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{season}_{\tau})}

Parameters:

Name	Type	Description	Default
`seasonality`	`int`	Int. Main frequency of the time series; Hourly 24, Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1.	required
`horizon_weight`		Tensor of size h, weight for each timestamp of the forecasting window.	`None`

`MASE.call`

__call__(y, y_hat, y_insample, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Tensor (batch_size, output_size), Actual values.	required
`y_hat`	`Tensor`	Tensor (batch_size, output_size)), Predicted values.	required
`y_insample`	`Tensor`	Tensor (batch_size, input_size), Actual insample values.	required
`mask`	`Union[Tensor, None]`	Tensor, Specifies date stamps per serie to consider in loss.	`None`

Returns:

Name	Type	Description
`mase`	`Tensor`	Tensor (single value).

Relative Mean Squared Error (relMSE)

`relMSE`

relMSE(y_train=None, horizon_weight=None)

Bases: BasePointLoss Relative Mean Squared Error Computes Relative Mean Squared Error (relMSE), as proposed by Hyndman & Koehler (2006) as an alternative to percentage errors, to avoid measure unstability.

\mathrm{relMSE}(\mathbf{y}, \mathbf{\hat{y}}, \mathbf{\hat{y}}^{benchmark}) = \frac{\mathrm{MSE}(\mathbf{y}, \mathbf{\hat{y}})}{\mathrm{MSE}(\mathbf{y}, \mathbf{\hat{y}}^{benchmark})}

Parameters:

Name	Type	Description	Default
`y_train`		Numpy array, deprecated.	`None`
`horizon_weight`		Tensor of size h, weight for each timestamp of the forecasting window.	`None`

`relMSE.call`

__call__(y, y_hat, y_benchmark, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Tensor (batch_size, output_size), Actual values.	required
`y_hat`	`Tensor`	Tensor (batch_size, output_size)), Predicted values.	required
`y_benchmark`	`Tensor`	Tensor (batch_size, output_size), Benchmark predicted values.	required
`mask`	`Union[Tensor, None]`	Tensor, Specifies date stamps per serie to consider in loss.	`None`

Returns:

Name	Type	Description
`relMSE`	`Tensor`	Tensor (single value).

4. Probabilistic Errors

These methods use statistical approaches for estimating unknown probability distributions using observed data. Maximum likelihood estimation involves finding the parameter values that maximize the likelihood function, which measures the probability of obtaining the observed data given the parameter values. MLE has good theoretical properties and efficiency under certain satisfied assumptions. On the non-parametric approach, quantile regression measures non-symmetrically deviation, producing under/over estimation.

Quantile Loss

`QuantileLoss`

QuantileLoss(q, horizon_weight=None)

Bases: BasePointLoss Quantile Loss. Computes the quantile loss between y and y_hat. QL measures the deviation of a quantile forecast. By weighting the absolute deviation in a non symmetric way, the loss pays more attention to under or over estimation. A common value for q is 0.5 for the deviation from the median (Pinball loss).

\mathrm{QL}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q)}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \Big( (1-q)\,( \hat{y}^{(q)}_{\tau} - y_{\tau} )_{+} + q\,( y_{\tau} - \hat{y}^{(q)}_{\tau} )_{+} \Big)

Parameters:

Name	Type	Description	Default
`q`	`float`	Between 0 and 1. The slope of the quantile loss, in the context of quantile regression, the q determines the conditional quantile level.	required
`horizon_weight`	`Optional[Tensor]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`QuantileLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Calculate quantile loss between actual and predicted values. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`y_insample`	`Union[Tensor, None]`	Actual insample values. Defaults to None.	`None`
`mask`	`Union[Tensor, None]`	Specifies datapoints to consider in loss. Defaults to None.	`None`

Returns:

Type	Description
`Tensor`	torch.Tensor: Quantile loss (single value).

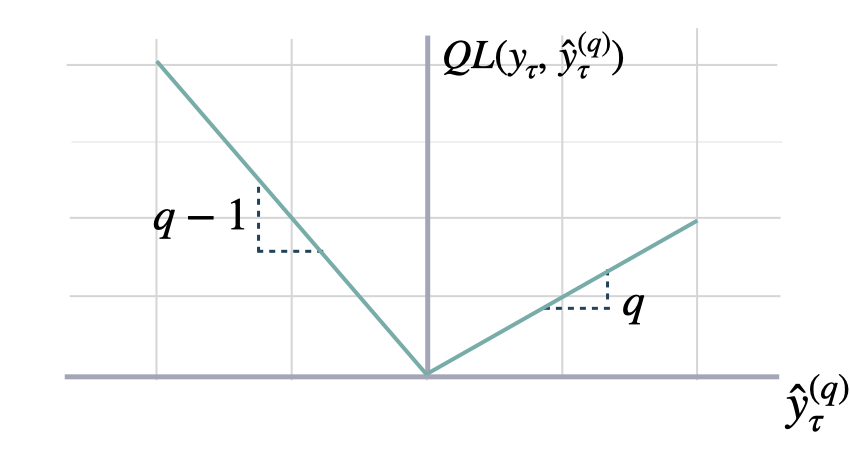
Multi Quantile Loss (MQLoss)

`MQLoss`

MQLoss(level=[80, 90], quantiles=None, horizon_weight=None)

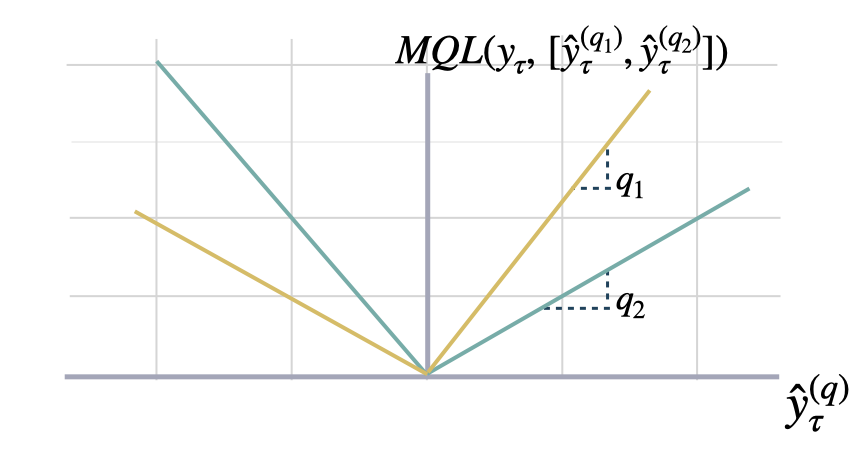
Bases: BasePointLoss Multi-Quantile loss Calculates the Multi-Quantile loss (MQL) between y and y_hat. MQL calculates the average multi-quantile Loss for a given set of quantiles, based on the absolute difference between predicted quantiles and observed values.

\mathrm{MQL}(\mathbf{y}_{\tau},[\mathbf{\hat{y}}^{(q_{1})}_{\tau}, ... ,\hat{y}^{(q_{n})}_{\tau}]) = \frac{1}{n} \sum_{q_{i}} \mathrm{QL}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q_{i})}_{\tau})

The limit behavior of MQL allows to measure the accuracy of a full predictive distribution

\\mathbf{\\hat{F}}\_{\\tau}

with the continuous ranked probability score (CRPS). This can be achieved through a numerical integration technique, that discretizes the quantiles and treats the CRPS integral with a left Riemann approximation, averaging over uniformly distanced quantiles.

\mathrm{CRPS}(y_{\tau}, \mathbf{\hat{F}}_{\tau}) = \int^{1}_{0} \mathrm{QL}(y_{\tau}, \hat{y}^{(q)}_{\tau}) dq

Parameters:

Name	Type	Description	Default
`level`	`List[int]`	Probability levels for prediction intervals. Defaults to [80, 90].	`[80, 90]`
`quantiles`	`Optional[List[float]]`	Alternative to level, quantiles to estimate from y distribution. Defaults to None.	`None`
`horizon_weight`	`Optional[Tensor]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`MQLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Computes the multi-quantile loss. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`y_insample`	`Union[Tensor, None]`	In-sample values. Defaults to None.	`None`
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Type	Description
`Tensor`	torch.Tensor: Multi-quantile loss (single value).

Implicit Quantile Loss (IQLoss)

`QuantileLayer`

QuantileLayer(num_output, cos_embedding_dim=128)

Bases: Module Implicit Quantile Layer from the paper IQN for Distributional Reinforcement Learning. Code from GluonTS: https://github.com/awslabs/gluonts/blob/61133ef6e2d88177b32ace4afc6843ab9a7bc8cd/src/gluonts/torch/distributions/implicit_quantile_network.py

`IQLoss`

IQLoss(
    cos_embedding_dim=64,
    concentration0=1.0,
    concentration1=1.0,
    horizon_weight=None,
)

Bases: QuantileLoss Implicit Quantile Loss. Computes the quantile loss between y and y_hat, with the quantile q provided as an input to the network. IQL measures the deviation of a quantile forecast. By weighting the absolute deviation in a non symmetric way, the loss pays more attention to under or over estimation.

\mathrm{QL}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q)}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \Big( (1-q)\,( \hat{y}^{(q)}_{\tau} - y_{\tau} )_{+} + q\,( y_{\tau} - \hat{y}^{(q)}_{\tau} )_{+} \Big)

Parameters:

Name	Type	Description	Default
`cos_embedding_dim`	`int`	Cosine embedding dimension. Defaults to 64.	`64`
`concentration0`	`float`	Beta distribution concentration parameter. Defaults to 1.0.	`1.0`
`concentration1`	`float`	Beta distribution concentration parameter. Defaults to 1.0.	`1.0`
`horizon_weight`	`Optional[Tensor]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`IQLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Calculate quantile loss between actual and predicted values. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`y_insample`	`Union[Tensor, None]`	Actual insample values. Defaults to None.	`None`
`mask`	`Union[Tensor, None]`	Specifies datapoints to consider in loss. Defaults to None.	`None`

Returns:

Type	Description
`Tensor`	torch.Tensor: Quantile loss (single value).

DistributionLoss

`DistributionLoss`

DistributionLoss(
    distribution,
    level=[80, 90],
    quantiles=None,
    num_samples=1000,
    return_params=False,
    horizon_weight=None,
    **distribution_kwargs
)

Bases: Module DistributionLoss This PyTorch module wraps the torch.distribution classes allowing it to interact with NeuralForecast models modularly. It shares the negative log-likelihood as the optimization objective and a sample method to generate empirically the quantiles defined by the level list. Additionally, it implements a distribution transformation that factorizes the scale-dependent likelihood parameters into a base scale and a multiplier efficiently learnable within the network’s non-linearities operating ranges. Available distributions:

Poisson
Normal
StudentT
NegativeBinomial
Tweedie
Bernoulli (Temporal Classifiers)
ISQF (Incremental Spline Quantile Function)

Parameters:

Name	Type	Description	Default
`distribution`	`str`	Identifier of a torch.distributions.Distribution class.	required
`level`	`float list`	Confidence levels for prediction intervals.	`[80, 90]`
`quantiles`	`float list`	Alternative to level list, target quantiles.	`None`
`num_samples`	`int`	Number of samples for the empirical quantiles.	`1000`
`return_params`	`bool`	Whether or not return the Distribution parameters.	`False`
`horizon_weight`	`Tensor`	Tensor of size h, weight for each timestamp of the forecasting window.	`None`

Returns:

Name	Type	Description
`tuple`		Tuple with tensors of ISQF distribution arguments.

`DistributionLoss.call`

__call__(y, distr_args, mask=None)

Computes the negative log-likelihood objective function. To estimate the following predictive distribution:

\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta) \quad \mathrm{and} \quad -\log(\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta))

where

\\theta

represents the distributions parameters. It aditionally summarizes the objective signal using a weighted average using the mask tensor. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`distr_args`	`Tensor`	Constructor arguments for the underlying Distribution type.	required
`loc`	`Optional[Tensor]`	Optional tensor, of the same shape as the batch_shape + event_shape. Defaults to None. of the resulting distribution.	required
`scale`	`Optional[Tensor]`	Optional tensor, of the same shape as the batch_shape+event_shape of the resulting distribution. Defaults to None.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`		Weighted loss function against which backpropagation will be performed.

Poisson Mixture Mesh (PMM)

`PMM`

PMM(
    n_components=10,
    level=[80, 90],
    quantiles=None,
    num_samples=1000,
    return_params=False,
    batch_correlation=False,
    horizon_correlation=False,
    weighted=False,
)

Bases: Module Poisson Mixture Mesh This Poisson Mixture statistical model assumes independence across groups of data

\\mathcal{G}={[g\_{i}]}

, and estimates relationships within the group.

\mathrm{P}\left(\mathbf{y}_{[b][t+1:t+H]}\right) = \prod_{ [g_{i}] \in \mathcal{G}} \mathrm{P} \left(\mathbf{y}_{[g_{i}][\tau]} \right) = \prod_{\beta\in[g_{i}]} \left(\sum_{k=1}^{K} w_k \prod_{(\beta,\tau) \in [g_i][t+1:t+H]} \mathrm{Poisson}(y_{\beta,\tau}, \hat{\lambda}_{\beta,\tau,k}) \right)

Parameters:

Name	Type	Description	Default
`n_components`	`int`	The number of mixture components. Defaults to 10.	`10`
`level`	`float list`	Confidence levels for prediction intervals. Defaults to [80, 90].	`[80, 90]`
`quantiles`	`float list`	Alternative to level list, target quantiles. Defaults to None.	`None`
`return_params`	`bool`	Whether or not return the Distribution parameters. Defaults to False.	`False`
`batch_correlation`	`bool`	Whether or not model batch correlations. Defaults to False.	`False`
`horizon_correlation`	`bool`	Whether or not model horizon correlations. Defaults to False.	`False`

`PMM.call`

__call__(y, distr_args, mask=None)

Computes the negative log-likelihood objective function. To estimate the following predictive distribution:

\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta) \quad \mathrm{and} \quad -\log(\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta))

where

\\theta

represents the distributions parameters. It aditionally summarizes the objective signal using a weighted average using the mask tensor. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`distr_args`	`Tensor`	Constructor arguments for the underlying Distribution type.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`		Weighted loss function against which backpropagation will be performed.

Gaussian Mixture Mesh (GMM)

`GMM`

GMM(
    n_components=1,
    level=[80, 90],
    quantiles=None,
    num_samples=1000,
    return_params=False,
    batch_correlation=False,
    horizon_correlation=False,
    weighted=False,
)

Bases: Module Gaussian Mixture Mesh This Gaussian Mixture statistical model assumes independence across groups of data

\\mathcal{G}={[g\_{i}]}

, and estimates relationships within the group.

\mathrm{P}\left(\mathbf{y}_{[b][t+1:t+H]}\right) = \prod_{ [g_{i}] \in \mathcal{G}} \mathrm{P}\left(\mathbf{y}_{[g_{i}][\tau]}\right)= \prod_{\beta\in[g_{i}]} \left(\sum_{k=1}^{K} w_k \prod_{(\beta,\tau) \in [g_i][t+1:t+H]} \mathrm{Gaussian}(y_{\beta,\tau}, \hat{\mu}_{\beta,\tau,k}, \sigma_{\beta,\tau,k})\right)

Parameters:

Name	Type	Description	Default
`n_components`	`int`	The number of mixture components. Defaults to 10.	`1`
`level`	`float list`	Confidence levels for prediction intervals. Defaults to [80, 90].	`[80, 90]`
`quantiles`	`float list`	Alternative to level list, target quantiles. Defaults to None.	`None`
`return_params`	`bool`	Whether or not return the Distribution parameters. Defaults to False.	`False`
`batch_correlation`	`bool`	Whether or not model batch correlations. Defaults to False.	`False`
`horizon_correlation`	`bool`	Whether or not model horizon correlations. Defaults to False.	`False`
`weighted`	`bool`	Whether or not model weighted components. Defaults to False.	`False`
`num_samples`	`int`	Number of samples for the empirical quantiles. Defaults to 1000.	`1000`

`GMM.call`

__call__(y, distr_args, mask=None)

Computes the negative log-likelihood objective function. To estimate the following predictive distribution:

\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta) \quad \mathrm{and} \quad -\log(\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta))

where

\\theta

represents the distributions parameters. It aditionally summarizes the objective signal using a weighted average using the mask tensor. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`distr_args`	`Tensor`	Constructor arguments for the underlying Distribution type.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`		Weighted loss function against which backpropagation will be performed.

Negative Binomial Mixture Mesh (NBMM)

`NBMM`

NBMM(
    n_components=1,
    level=[80, 90],
    quantiles=None,
    num_samples=1000,
    return_params=False,
    weighted=False,
)

Bases: Module Negative Binomial Mixture Mesh This N. Binomial Mixture statistical model assumes independence across groups of data

\\mathcal{G}={[g\_{i}]}

, and estimates relationships within the group.

\mathrm{P}\left(\mathbf{y}_{[b][t+1:t+H]}\right) = \prod_{ [g_{i}] \in \mathcal{G}} \mathrm{P}\left(\mathbf{y}_{[g_{i}][\tau]}\right)= \prod_{\beta\in[g_{i}]} \left(\sum_{k=1}^{K} w_k \prod_{(\beta,\tau) \in [g_i][t+1:t+H]} \mathrm{NBinomial}(y_{\beta,\tau}, \hat{r}_{\beta,\tau,k}, \hat{p}_{\beta,\tau,k})\right)

Parameters:

Name	Type	Description	Default
`n_components`	`int`	The number of mixture components. Defaults to 10.	`1`
`level`	`float list`	Confidence levels for prediction intervals. Defaults to [80, 90].	`[80, 90]`
`quantiles`	`float list`	Alternative to level list, target quantiles. Defaults to None.	`None`
`return_params`	`bool`	Whether or not return the Distribution parameters. Defaults to False.	`False`
`weighted`	`bool`	Whether or not model weighted components. Defaults to False.	`False`
`num_samples`	`int`	Number of samples for the empirical quantiles. Defaults to 1000.	`1000`

`NBMM.call`

__call__(y, distr_args, mask=None)

Computes the negative log-likelihood objective function. To estimate the following predictive distribution:

\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta) \quad \mathrm{and} \quad -\log(\mathrm{P}(\mathbf{y}_{\tau}\,|\,\theta))

where

\\theta

represents the distributions parameters. It aditionally summarizes the objective signal using a weighted average using the mask tensor. Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`distr_args`	`Tensor`	Constructor arguments for the underlying Distribution type.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`		Weighted loss function against which backpropagation will be performed.

5. Robustified Errors

Huber Loss

`HuberLoss`

HuberLoss(delta=1.0, horizon_weight=None)

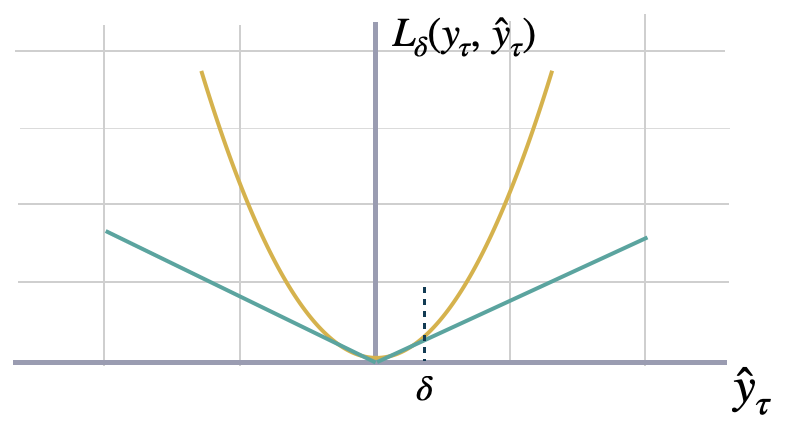
Bases: BasePointLoss Huber Loss The Huber loss, employed in robust regression, is a loss function that exhibits reduced sensitivity to outliers in data when compared to the squared error loss. This function is also refered as SmoothL1. The Huber loss function is quadratic for small errors and linear for large errors, with equal values and slopes of the different sections at the two points where

(y\_{\\tau}-\\hat{y}_{\\tau})^{2}

|y_{\\tau}-\\hat{y}\_{\\tau}|

L_{\delta}(y_{\tau},\; \hat{y}_{\tau}) =\begin{cases}{\frac{1}{2}}(y_{\tau}-\hat{y}_{\tau})^{2}\;{\text{for }}|y_{\tau}-\hat{y}_{\tau}|\leq \delta \\ \delta \ \cdot \left(|y_{\tau}-\hat{y}_{\tau}|-{\frac {1}{2}}\delta \right),\;{\text{otherwise.}}\end{cases}

where

\\delta

is a threshold parameter that determines the point at which the loss transitions from quadratic to linear, and can be tuned to control the trade-off between robustness and accuracy in the predictions. Parameters:

Name	Type	Description	Default
`delta`	`float`	Specifies the threshold at which to change between delta-scaled L1 and L2 loss. Defaults to 1.0.	`1.0`
`horizon_weight`	`Union[Tensor, None]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`HuberLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`	`Tensor`	Huber loss.

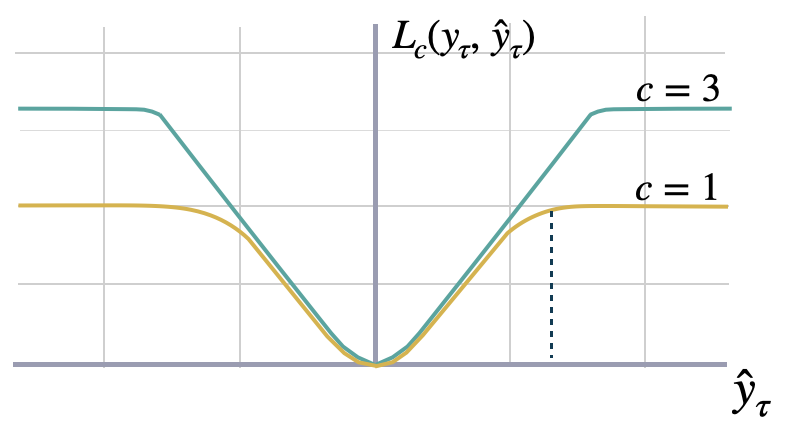
Tukey Loss

`TukeyLoss`

TukeyLoss(c=4.685, normalize=True)

Bases: BasePointLoss Tukey Loss The Tukey loss function, also known as Tukey’s biweight function, is a robust statistical loss function used in robust statistics. Tukey’s loss exhibits quadratic behavior near the origin, like the Huber loss; however, it is even more robust to outliers as the loss for large residuals remains constant instead of scaling linearly. The parameter

c

in Tukey’s loss determines the ”saturation” point of the function: Higher values of

c

enhance sensitivity, while lower values increase resistance to outliers.

L_{c}(y_{\tau},\; \hat{y}_{\tau}) =\begin{cases}{ \frac{c^{2}}{6}} \left[1-(\frac{y_{\tau}-\hat{y}_{\tau}}{c})^{2} \right]^{3} \;\text{for } |y_{\tau}-\hat{y}_{\tau}|\leq c \\ \frac{c^{2}}{6} \qquad \text{otherwise.} \end{cases}

Please note that the Tukey loss function assumes the data to be stationary or normalized beforehand. If the error values are excessively large, the algorithm may need help to converge during optimization. It is advisable to employ small learning rates. Parameters:

Name	Type	Description	Default
`c`	`float`	Specifies the Tukey loss’ threshold on which residuals are no longer considered. Defaults to 4.685.	`4.685`
`normalize`	`bool`	Wether normalization is performed within Tukey loss’ computation. Defaults to True.	`True`

`TukeyLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`	`Tensor`	Tukey loss.

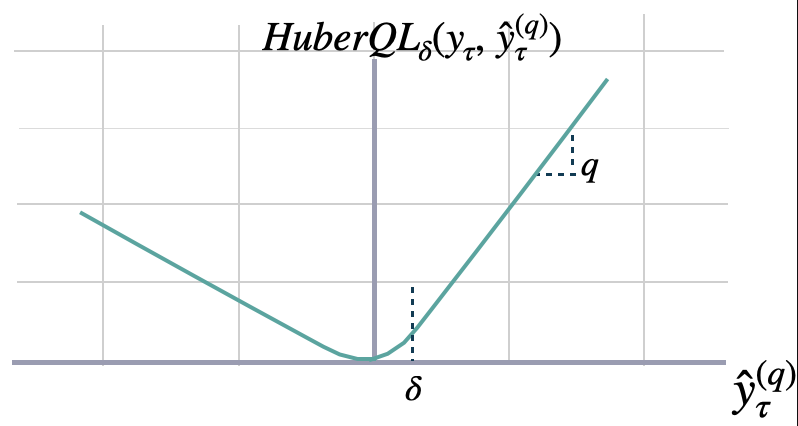
Huberized Quantile Loss

`HuberQLoss`

HuberQLoss(q, delta=1.0, horizon_weight=None)

Bases: BasePointLoss Huberized Quantile Loss The Huberized quantile loss is a modified version of the quantile loss function that combines the advantages of the quantile loss and the Huber loss. It is commonly used in regression tasks, especially when dealing with data that contains outliers or heavy tails. The Huberized quantile loss between y and y_hat measure the Huber Loss in a non-symmetric way. The loss pays more attention to under/over-estimation depending on the quantile parameter

q

; and controls the trade-off between robustness and accuracy in the predictions with the parameter

delta

\mathrm{HuberQL}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q)}_{\tau}) = (1-q)\, L_{\delta}(y_{\tau},\; \hat{y}^{(q)}_{\tau}) \mathbb{1}\{ \hat{y}^{(q)}_{\tau} \geq y_{\tau} \} + q\, L_{\delta}(y_{\tau},\; \hat{y}^{(q)}_{\tau}) \mathbb{1}\{ \hat{y}^{(q)}_{\tau} < y_{\tau} \}

Parameters:

Name	Type	Description	Default
`delta`	`float`	Specifies the threshold at which to change between delta-scaled L1 and L2 loss. Defaults to 1.0.	`1.0`
`q`	`float`	The slope of the quantile loss, in the context of quantile regression, the q determines the conditional quantile level. Defaults to 0.5.	required
`horizon_weight`	`Union[Tensor, None]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`HuberQLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`	`Tensor`	HuberQLoss.

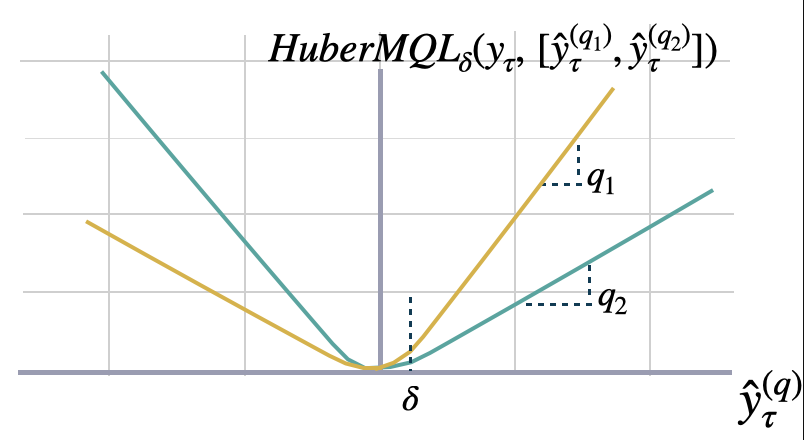
Huberized MQLoss

`HuberMQLoss`

HuberMQLoss(level=[80, 90], quantiles=None, delta=1.0, horizon_weight=None)

Bases: BasePointLoss Huberized Multi-Quantile loss The Huberized Multi-Quantile loss (HuberMQL) is a modified version of the multi-quantile loss function that combines the advantages of the quantile loss and the Huber loss. HuberMQL is commonly used in regression tasks, especially when dealing with data that contains outliers or heavy tails. The loss function pays more attention to under/over-estimation depending on the quantile list

[q\_{1},q\_{2},\\dots]

parameter. It controls the trade-off between robustness and prediction accuracy with the parameter

\\delta

\mathrm{HuberMQL}_{\delta}(\mathbf{y}_{\tau},[\mathbf{\hat{y}}^{(q_{1})}_{\tau}, ... ,\hat{y}^{(q_{n})}_{\tau}]) = \frac{1}{n} \sum_{q_{i}} \mathrm{HuberQL}_{\delta}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q_{i})}_{\tau})

Parameters:

Name	Type	Description	Default
`level`	`int list`	Probability levels for prediction intervals (Defaults median). Defaults to [80, 90].	`[80, 90]`
`quantiles`	`float list`	Alternative to level, quantiles to estimate from y distribution. Defaults to None.	`None`
`delta`	`float`	Specifies the threshold at which to change between delta-scaled L1 and L2 loss. Defaults to 1.0.	`1.0`
`horizon_weight`	`Union[Tensor, None]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`

`HuberMQLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`	`Tensor`	HuberMQLoss.

Huberized IQLoss

`HuberIQLoss`

HuberIQLoss(
    cos_embedding_dim=64,
    concentration0=1.0,
    concentration1=1.0,
    delta=1.0,
    horizon_weight=None,
)

Bases: HuberQLoss Implicit Huber Quantile Loss Computes the huberized quantile loss between y and y_hat, with the quantile q provided as an input to the network. HuberIQLoss measures the deviation of a huberized quantile forecast. By weighting the absolute deviation in a non symmetric way, the loss pays more attention to under or over estimation.

\mathrm{HuberIQL}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q)}_{\tau}) = (1-q)\, L_{\delta}(y_{\tau},\; \hat{y}^{(q)}_{\tau}) \mathbb{1}\{ \hat{y}^{(q)}_{\tau} \geq y_{\tau} \} + q\, L_{\delta}(y_{\tau},\; \hat{y}^{(q)}_{\tau}) \mathbb{1}\{ \hat{y}^{(q)}_{\tau} < y_{\tau} \}

Parameters:

Name	Type	Description	Default
`quantile_sampling`	`str`	Sampling distribution used to sample the quantiles during training. Choose from [‘uniform’, ‘beta’]. Defaults to ‘uniform’.	required
`horizon_weight`	`Union[Tensor, None]`	Tensor of size h, weight for each timestamp of the forecasting window. Defaults to None.	`None`
`delta`	`float`	Specifies the threshold at which to change between delta-scaled L1 and L2 loss. Defaults to 1.0.	`1.0`

`HuberIQLoss.call`

__call__(y, y_hat, y_insample=None, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`	`Tensor`	HuberQLoss.

6. Others

Accuracy

`Accuracy`

Accuracy()

Bases: BasePointLoss Accuracy Computes the accuracy between categorical y and y_hat. This evaluation metric is only meant for evalution, as it is not differentiable.

\mathrm{Accuracy}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \mathrm{1}\{\mathbf{y}_{\tau}==\mathbf{\hat{y}}_{\tau}\}

`Accuracy.call`

__call__(y, y_hat, y_insample, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per serie to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`	`Tensor`	Accuracy.

Scaled Continuous Ranked Probability Score (sCRPS)

`sCRPS`

sCRPS(level=[80, 90], quantiles=None)

Bases: BasePointLoss Scaled Continues Ranked Probability Score Calculates a scaled variation of the CRPS, as proposed by Rangapuram (2021), to measure the accuracy of predicted quantiles y_hat compared to the observation y. This metric averages percentual weighted absolute deviations as defined by the quantile losses.

\mathrm{sCRPS}(\mathbf{\hat{y}}^{(q)}_{\tau}, \mathbf{y}_{\tau}) = \frac{2}{N} \sum_{i} \int^{1}_{0} \frac{\mathrm{QL}(\mathbf{\hat{y}}^{(q}_{\tau} y_{i,\tau})_{q}}{\sum_{i} | y_{i,\tau} |} dq

where

\\mathbf{\\hat{y}}^{(q}_{\\tau}

is the estimated quantile, and

y_{i,\\tau}

are the target variable realizations. Parameters:

Name	Type	Description	Default
`level`	`int list`	Probability levels for prediction intervals (Defaults median). Defaults to [80, 90].	`[80, 90]`
`quantiles`	`float list`	Alternative to level, quantiles to estimate from y distribution. Defaults to None.	`None`

`sCRPS.call`

__call__(y, y_hat, y_insample, mask=None)

Parameters:

Name	Type	Description	Default
`y`	`Tensor`	Actual values.	required
`y_hat`	`Tensor`	Predicted values.	required
`mask`	`Union[Tensor, None]`	Specifies date stamps per series to consider in loss. Defaults to None.	`None`

Returns:

Name	Type	Description
`float`	`Tensor`	sCRPS.

Getting Started

Capabilities

Tutorials

Use cases

API Reference

​BasePointLoss

​1. Scale-dependent Errors

​Mean Absolute Error (MAE)

​MAE

​MAE.__call__

​Mean Squared Error (MSE)

​MSE

​MSE.__call__

​Root Mean Squared Error (RMSE)

​RMSE

​RMSE.__call__

​2. Percentage errors

​Mean Absolute Percentage Error (MAPE)

​MAPE

​MAPE.__call__

​Symmetric MAPE (sMAPE)

​SMAPE

​SMAPE.__call__

​3. Scale-independent Errors

​Mean Absolute Scaled Error (MASE)

​MASE

​MASE.__call__

​Relative Mean Squared Error (relMSE)

​relMSE

​relMSE.__call__

​4. Probabilistic Errors

​Quantile Loss

​QuantileLoss

​QuantileLoss.__call__

​Multi Quantile Loss (MQLoss)

​MQLoss

​MQLoss.__call__

​Implicit Quantile Loss (IQLoss)

​QuantileLayer

​IQLoss

​IQLoss.__call__

​DistributionLoss

​DistributionLoss

​DistributionLoss.__call__

​Poisson Mixture Mesh (PMM)

​PMM

​PMM.__call__

​Gaussian Mixture Mesh (GMM)

​GMM

​GMM.__call__

​Negative Binomial Mixture Mesh (NBMM)

​NBMM

​NBMM.__call__

​5. Robustified Errors

​Huber Loss

​HuberLoss

​HuberLoss.__call__

​Tukey Loss

​TukeyLoss

​TukeyLoss.__call__

​Huberized Quantile Loss

​HuberQLoss

​HuberQLoss.__call__

​Huberized MQLoss

​HuberMQLoss

​HuberMQLoss.__call__

​Huberized IQLoss

​HuberIQLoss

​HuberIQLoss.__call__

​6. Others

​Accuracy

​Accuracy

​Accuracy.__call__

​Scaled Continuous Ranked Probability Score (sCRPS)

​sCRPS

​sCRPS.__call__

`BasePointLoss`

1. Scale-dependent Errors

Mean Absolute Error (MAE)

`MAE`

`MAE.call`

Mean Squared Error (MSE)

`MSE`

`MSE.call`

Root Mean Squared Error (RMSE)

`RMSE`

`RMSE.call`

2. Percentage errors

Mean Absolute Percentage Error (MAPE)

`MAPE`

`MAPE.call`

Symmetric MAPE (sMAPE)

`SMAPE`

`SMAPE.call`

3. Scale-independent Errors

Mean Absolute Scaled Error (MASE)

`MASE`

`MASE.call`

Relative Mean Squared Error (relMSE)

`relMSE`

`relMSE.call`

4. Probabilistic Errors

Quantile Loss

`QuantileLoss`

`QuantileLoss.call`

Multi Quantile Loss (MQLoss)

`MQLoss`

`MQLoss.call`

Implicit Quantile Loss (IQLoss)

`QuantileLayer`

`IQLoss`

`IQLoss.call`

DistributionLoss

`DistributionLoss`

`DistributionLoss.call`

Poisson Mixture Mesh (PMM)

`PMM`

`PMM.call`

Gaussian Mixture Mesh (GMM)

`GMM`

`GMM.call`

Negative Binomial Mixture Mesh (NBMM)

`NBMM`

`NBMM.call`

5. Robustified Errors

Huber Loss

`HuberLoss`

`HuberLoss.call`

Tukey Loss

`TukeyLoss`

`TukeyLoss.call`

Huberized Quantile Loss

`HuberQLoss`

`HuberQLoss.call`

Huberized MQLoss

`HuberMQLoss`

`HuberMQLoss.call`

Huberized IQLoss

`HuberIQLoss`

`HuberIQLoss.call`

6. Others

Accuracy

`Accuracy`

`Accuracy.call`

Scaled Continuous Ranked Probability Score (sCRPS)

`sCRPS`

`sCRPS.call`