Probabilistic forecasting is a natural answer to quantify the uncertainty of target variable’s future. The task requires to model the following conditional predictive distribution: P(yt+1:t+H  ∣  y:t)\mathbb{P}(\mathbf{y}_{t+1:t+H} \;|\; \mathbf{y}_{:t}) We will show you how to tackle the task with NeuralForecast by combining a classic Long Short Term Memory Network (LSTM) and the Neural Hierarchical Interpolation (NHITS) with the multi quantile loss function (MQLoss). MQLoss(yτ,[y^τ(q1),y^τ(q2),…,y^τ(Q)])=1H∑qQL(yτ,y^τ(q))\mathrm{MQLoss}(y_{\tau}, [\hat{y}^{(q1)}_{\tau},\hat{y}^{(q2)}_{\tau},\dots,\hat{y}^{(Q)}_{\tau}]) = \frac{1}{H} \sum_{q} \mathrm{QL}(y_{\tau}, \hat{y}^{(q)}_{\tau}) In this notebook we will:
1. Install NeuralForecast Library
2. Explore the M4-Hourly data.
3. Train the LSTM and NHITS
4. Visualize the LSTM/NHITS prediction intervals. You can run these experiments using GPU with Google Colab. Open In Colab

​
1. Installing NeuralForecast

!pip install neuralforecast

​
Useful functions

The plot_grid auxiliary function defined below will be useful to plot different time series, and different models’ forecasts. 
import logging
import warnings

import torch
from utilsforecast.plotting import plot_series

warnings.filterwarnings("ignore")

​
2. Loading M4 Data

For testing purposes, we will use the Hourly dataset from the M4 competition.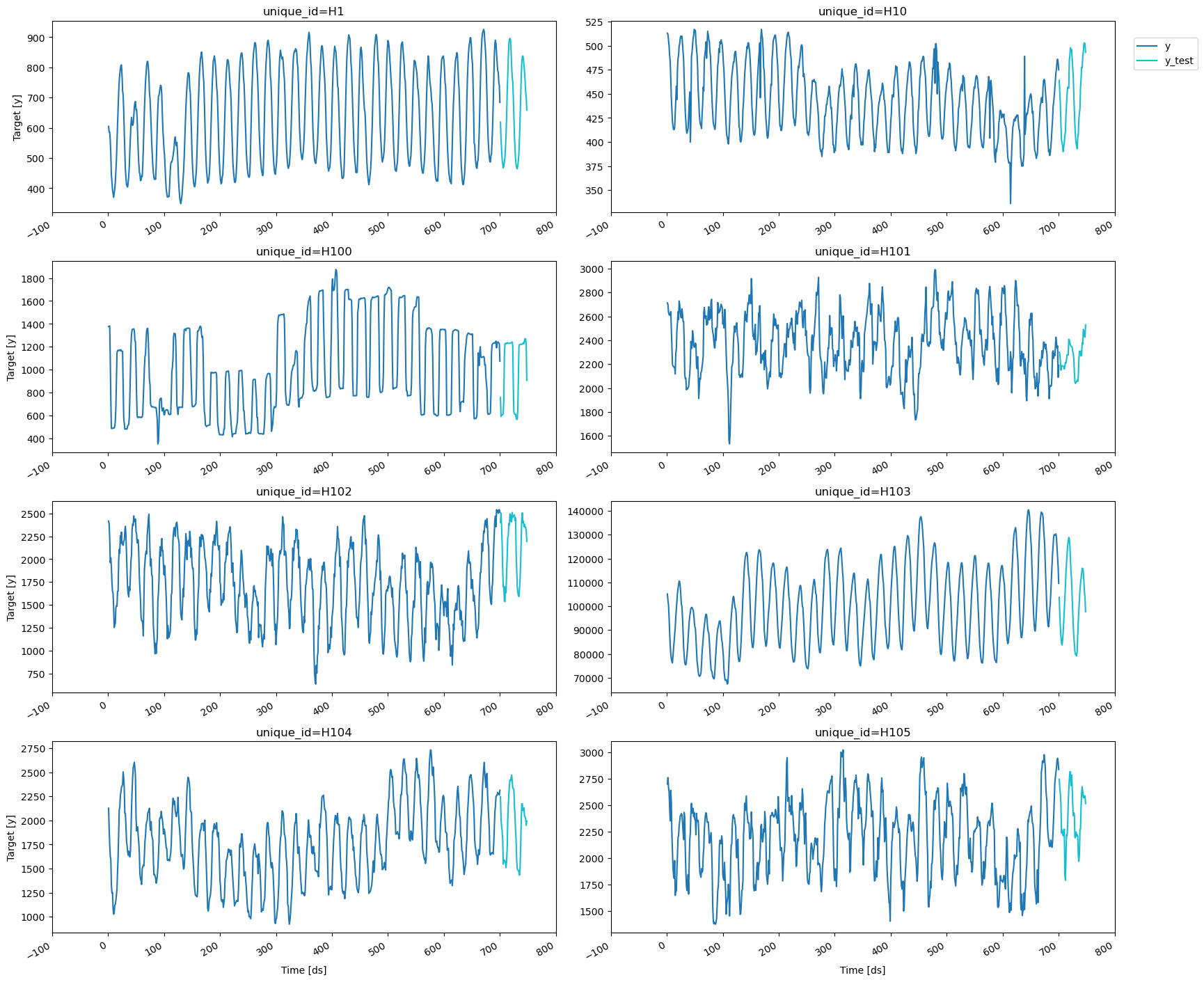 
import pandas as pd

Y_train_df = pd.read_csv('https://auto-arima-results.s3.amazonaws.com/M4-Hourly.csv')
Y_test_df = pd.read_csv(
    'https://auto-arima-results.s3.amazonaws.com/M4-Hourly-test.csv'
).rename(columns={'y': 'y_test'})
In this example we will use a subset of the data to avoid waiting too long. You can modify the number of series if you want. 
n_series = 8
uids = Y_train_df['unique_id'].unique()[:n_series]
Y_train_df = Y_train_df.query('unique_id in @uids')
Y_test_df = Y_test_df.query('unique_id in @uids')

plot_series(Y_train_df, Y_test_df)

​
3. Model Training

The core.NeuralForecast provides a high-level interface with our collection of PyTorch models. NeuralForecast is instantiated with a list of models=[LSTM(...), NHITS(...)], configured for the forecasting task.
  • The horizon parameter controls the number of steps ahead of the predictions, in this example 48 hours ahead (2 days).
  • The MQLoss with levels=[80,90] specializes the network’s output into the 80% and 90% prediction intervals.
  • The max_steps=2000, controls the duration of the network’s training.
For more network’s instantiation details check their documentation. 
from neuralforecast import NeuralForecast
from neuralforecast.losses.pytorch import MQLoss
from neuralforecast.models import LSTM, NHITS

logging.getLogger('pytorch_lightning').setLevel(logging.ERROR)
torch.set_float32_matmul_precision('high')

horizon = 48
levels = [80, 90]
models = [LSTM(input_size=3*horizon, h=horizon,
               loss=MQLoss(level=levels), max_steps=1000),
          NHITS(input_size=7*horizon, h=horizon,
                n_freq_downsample=[24, 12, 1],
                loss=MQLoss(level=levels), max_steps=2000),]
nf = NeuralForecast(models=models, freq=1)

Seed set to 1
Seed set to 1
All the models of the library are global, meaning that all time series in Y_train_df is used during a shared optimization to train a single model with shared parameters. This is the most common practice in the forecasting literature for deep learning models, and it is known as “cross-learning”. 
nf.fit(df=Y_train_df)

Y_hat_df = nf.predict()
Y_hat_df.head()

Predicting: |          | 0/? [00:00<?, ?it/s]

Predicting: |          | 0/? [00:00<?, ?it/s]
unique_iddsLSTM-medianLSTM-lo-90LSTM-lo-80LSTM-hi-80LSTM-hi-90NHITS-medianNHITS-lo-90NHITS-lo-80NHITS-hi-80NHITS-hi-90
0H1701650.919861526.705933551.696289748.392456777.889526615.786743582.732117584.717468640.011841647.147034
1H1702547.724487439.353394463.725464638.429626663.398987569.632324524.486023522.324402578.411560594.515076
2H1703514.851074421.289917443.166443589.451782608.560425518.858887503.183411501.016968536.081543549.701050
3H1704485.141418403.336914421.090546547.966492567.057800495.627869476.579742468.514069498.171600527.931091
4H1705462.695831383.011108399.126282522.579224543.981750481.584534468.134857472.723450496.198975513.859985
Y_test_df = Y_test_df.merge(Y_hat_df, how='left', on=['unique_id', 'ds']).rename(columns=lambda x: x.replace('-median', ''))

​
4. Plotting Predictions

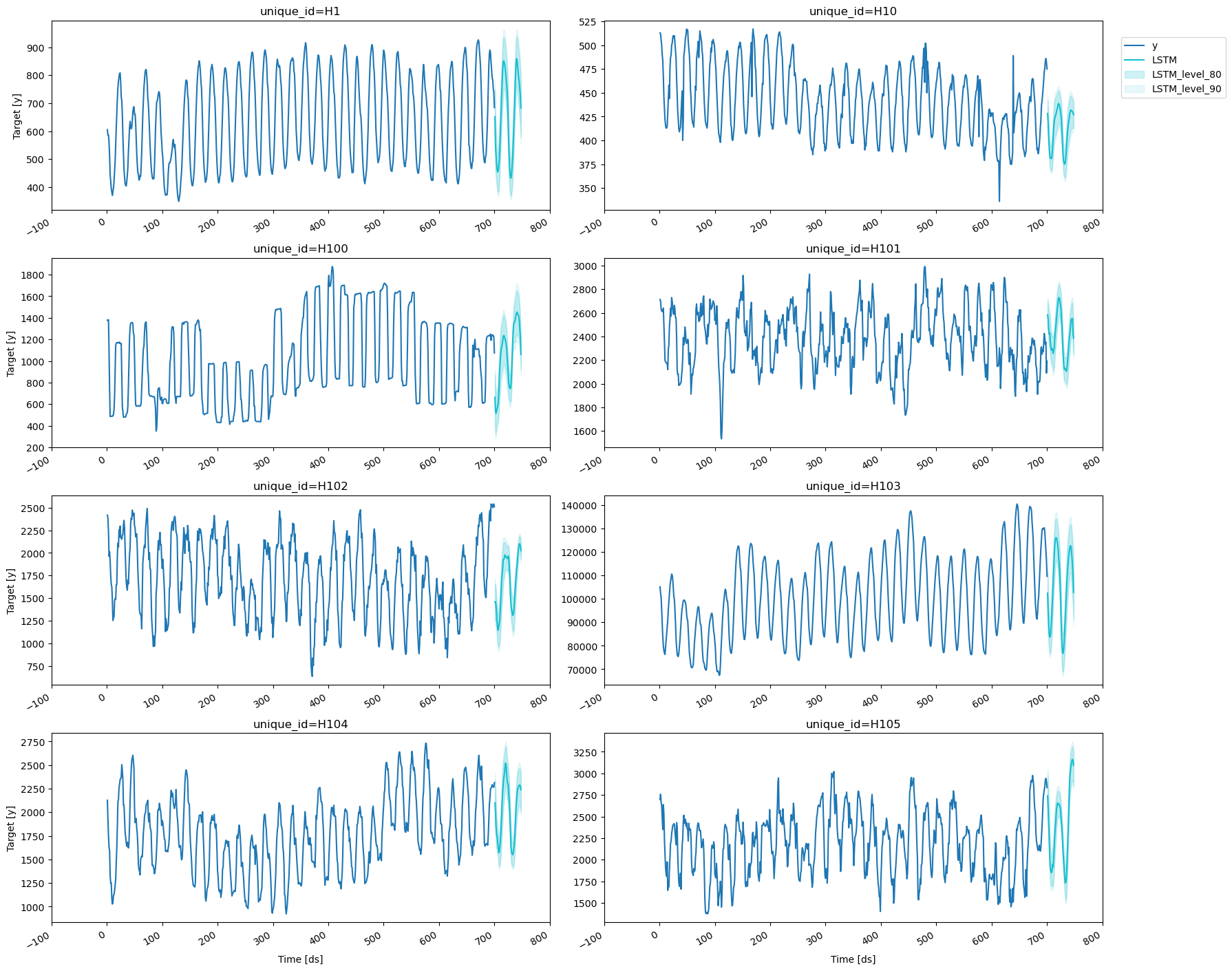
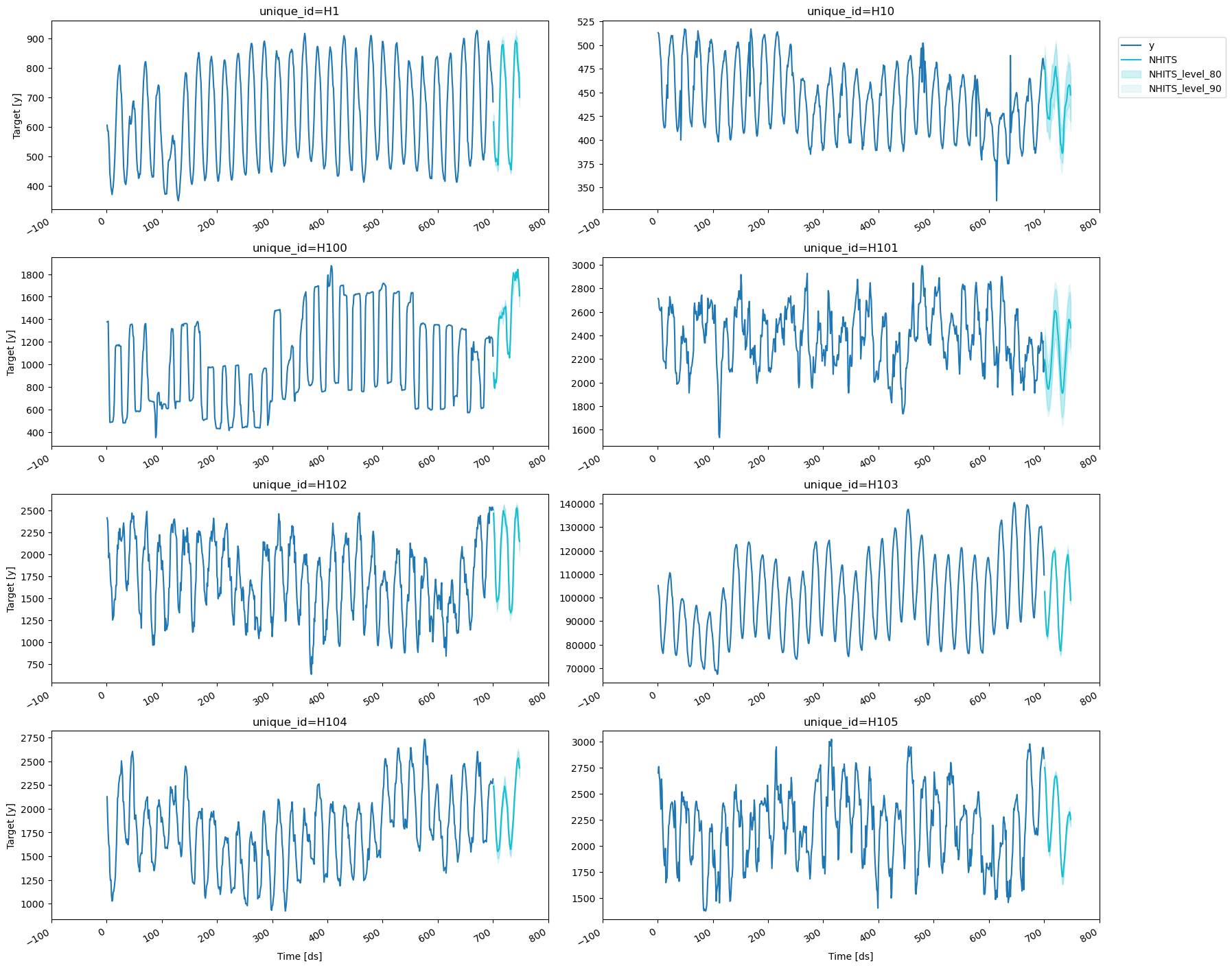
Here we finalize our analysis by plotting the prediction intervals and verifying that both the LSTM and NHITS are giving excellent results. Consider the output [NHITS-lo-90.0, NHITS-hi-90.0], that represents the 80% prediction interval of the NHITS network; its lower limit gives the 5th percentile (or 0.05 quantile) while its upper limit gives the 95th percentile (or 0.95 quantile). For well-trained models we expect that the target values lie within the interval 90% of the time.

​
LSTM

plot_series(Y_train_df, Y_test_df, level=levels, models=['LSTM'])

​
NHITS

plot_series(Y_train_df, Y_test_df, level=levels, models=['NHITS'])

​
References