The most important train signal is the forecast error, which is the difference between the observed value yτy_{\tau} and the prediction y^τ\hat{y}_{\tau}, at time yτy_{\tau}: eτ=yτ−y^ττ∈{t+1,…,t+H}e_{\tau} = y_{\tau}-\hat{y}_{\tau} \qquad \qquad \tau \in \{t+1,\dots,t+H \} The train loss summarizes the forecast errors in different evaluation metrics.

​
1. Scale-dependent Errors

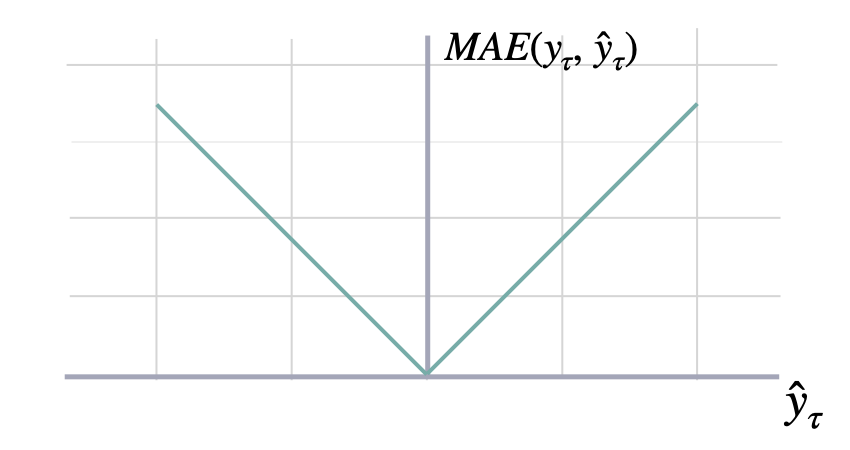
These metrics are on the same scale as the data.

​
Mean Absolute Error

source

​
mae

 mae (y:numpy.ndarray, y_hat:numpy.ndarray,
      weights:Optional[numpy.ndarray]=None, axis:Optional[int]=None)
*Mean Absolute Error Calculates Mean Absolute Error between y and y_hat. MAE measures the relative prediction accuracy of a forecasting method by calculating the deviation of the prediction and the true value at a given time and averages these devations over the length of the series. MAE(yτ,y^τ)=1H∑τ=t+1t+H∣yτ−y^τ∣\mathrm{MAE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} |y_{\tau} - \hat{y}_{\tau}| Parameters:
y: numpy array, Actual values.
y_hat: numpy array, Predicted values.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
mae: numpy array, (single value).*

​
Mean Squared Error

source

​
mse

 mse (y:numpy.ndarray, y_hat:numpy.ndarray,
      weights:Optional[numpy.ndarray]=None, axis:Optional[int]=None)
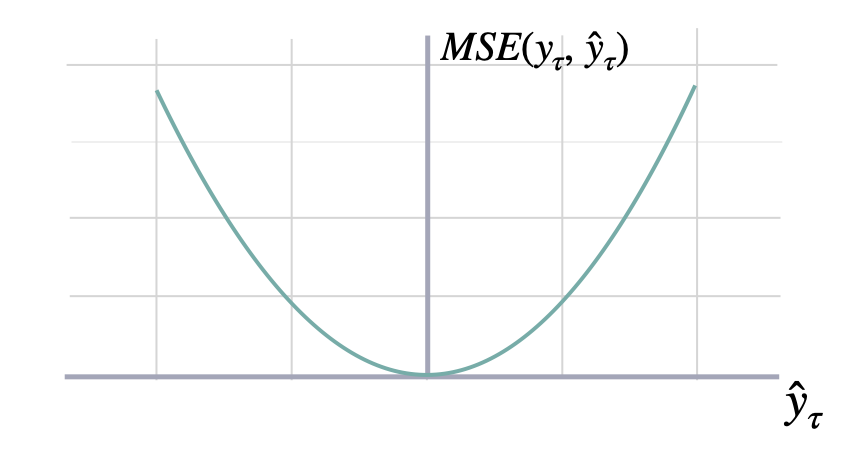
*Mean Squared Error Calculates Mean Squared Error between y and y_hat. MSE measures the relative prediction accuracy of a forecasting method by calculating the squared deviation of the prediction and the true value at a given time, and averages these devations over the length of the series. MSE(yτ,y^τ)=1H∑τ=t+1t+H(yτ−y^τ)2\mathrm{MSE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} (y_{\tau} - \hat{y}_{\tau})^{2} Parameters:
y: numpy array, Actual values.
y_hat: numpy array, Predicted values.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
mse: numpy array, (single value).*

​
Root Mean Squared Error

source

​
rmse

 rmse (y:numpy.ndarray, y_hat:numpy.ndarray,
       weights:Optional[numpy.ndarray]=None, axis:Optional[int]=None)
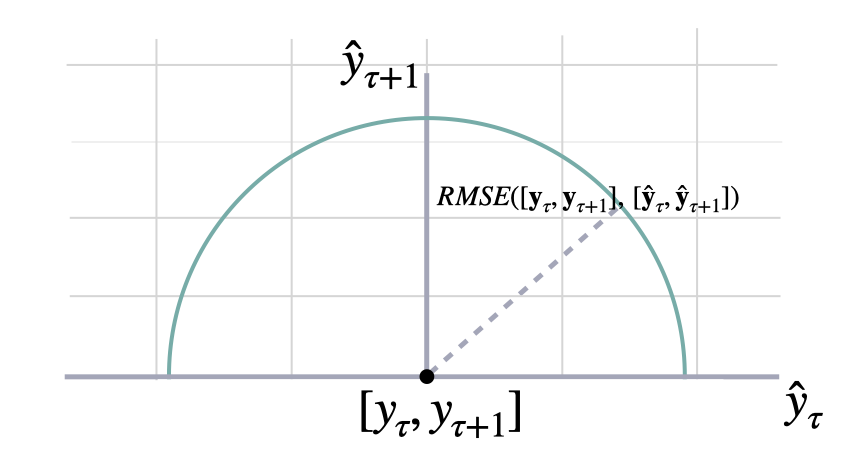
*Root Mean Squared Error Calculates Root Mean Squared Error between y and y_hat. RMSE measures the relative prediction accuracy of a forecasting method by calculating the squared deviation of the prediction and the observed value at a given time and averages these devations over the length of the series. Finally the RMSE will be in the same scale as the original time series so its comparison with other series is possible only if they share a common scale. RMSE has a direct connection to the L2 norm. RMSE(yτ,y^τ)=1H∑τ=t+1t+H(yτ−y^τ)2\mathrm{RMSE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \sqrt{\frac{1}{H} \sum^{t+H}_{\tau=t+1} (y_{\tau} - \hat{y}_{\tau})^{2}} Parameters:
y: numpy array, Actual values.
y_hat: numpy array, Predicted values.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
rmse: numpy array, (single value).*

​
2. Percentage errors

These metrics are unit-free, suitable for comparisons across series.

​
Mean Absolute Percentage Error

source

​
mape

 mape (y:numpy.ndarray, y_hat:numpy.ndarray,
       weights:Optional[numpy.ndarray]=None, axis:Optional[int]=None)
*Mean Absolute Percentage Error Calculates Mean Absolute Percentage Error between y and y_hat. MAPE measures the relative prediction accuracy of a forecasting method by calculating the percentual deviation of the prediction and the observed value at a given time and averages these devations over the length of the series. The closer to zero an observed value is, the higher penalty MAPE loss assigns to the corresponding error. MAPE(yτ,y^τ)=1H∑τ=t+1t+H∣yτ−y^τ∣∣yτ∣\mathrm{MAPE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \frac{|y_{\tau}-\hat{y}_{\tau}|}{|y_{\tau}|} Parameters:
y: numpy array, Actual values.
y_hat: numpy array, Predicted values.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
mape: numpy array, (single value).*

​
SMAPE

source

​
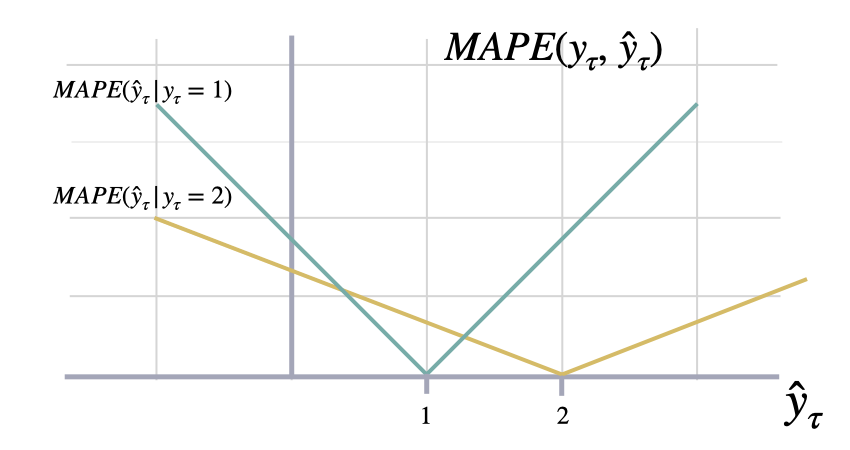
smape

 smape (y:numpy.ndarray, y_hat:numpy.ndarray,
        weights:Optional[numpy.ndarray]=None, axis:Optional[int]=None)
*Symmetric Mean Absolute Percentage Error Calculates Symmetric Mean Absolute Percentage Error between y and y_hat. SMAPE measures the relative prediction accuracy of a forecasting method by calculating the relative deviation of the prediction and the observed value scaled by the sum of the absolute values for the prediction and observed value at a given time, then averages these devations over the length of the series. This allows the SMAPE to have bounds between 0% and 200% which is desirable compared to normal MAPE that may be undetermined when the target is zero. sMAPE2(yτ,y^τ)=1H∑τ=t+1t+H∣yτ−y^τ∣∣yτ∣+∣y^τ∣\mathrm{sMAPE}_{2}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \frac{|y_{\tau}-\hat{y}_{\tau}|}{|y_{\tau}|+|\hat{y}_{\tau}|} Parameters:
y: numpy array, Actual values.
y_hat: numpy array, Predicted values.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
smape: numpy array, (single value). References:
Makridakis S., “Accuracy measures: theoretical and practical concerns”.*

​
3. Scale-independent Errors

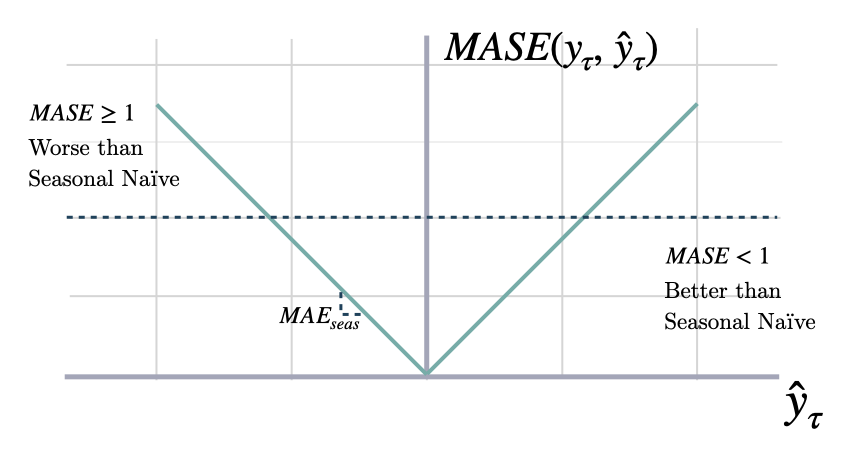
These metrics measure the relative improvements versus baselines.

​
Mean Absolute Scaled Error

source

​
mase

 mase (y:numpy.ndarray, y_hat:numpy.ndarray, y_train:numpy.ndarray,
       seasonality:int, weights:Optional[numpy.ndarray]=None,
       axis:Optional[int]=None)
*Mean Absolute Scaled Error Calculates the Mean Absolute Scaled Error between y and y_hat. MASE measures the relative prediction accuracy of a forecasting method by comparinng the mean absolute errors of the prediction and the observed value against the mean absolute errors of the seasonal naive model. The MASE partially composed the Overall Weighted Average (OWA), used in the M4 Competition. MASE(yτ,y^τ,y^τseason)=1H∑τ=t+1t+H∣yτ−y^τ∣MAE(yτ,y^τseason)\mathrm{MASE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}, \mathbf{\hat{y}}^{season}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \frac{|y_{\tau}-\hat{y}_{\tau}|}{\mathrm{MAE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{season}_{\tau})} Parameters:
y: numpy array, (batch_size, output_size), Actual values.
y_hat: numpy array, (batch_size, output_size)), Predicted values.
y_insample: numpy array, (batch_size, input_size), Actual insample Seasonal Naive predictions.
seasonality: int. Main frequency of the time series; Hourly 24, Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
mase: numpy array, (single value). References:
Rob J. Hyndman, & Koehler, A. B. “Another look at measures of forecast accuracy”.
Spyros Makridakis, Evangelos Spiliotis, Vassilios Assimakopoulos, “The M4 Competition: 100,000 time series and 61 forecasting methods”.*

​
Relative Mean Absolute Error

source

​
rmae

 rmae (y:numpy.ndarray, y_hat1:numpy.ndarray, y_hat2:numpy.ndarray,
       weights:Optional[numpy.ndarray]=None, axis:Optional[int]=None)
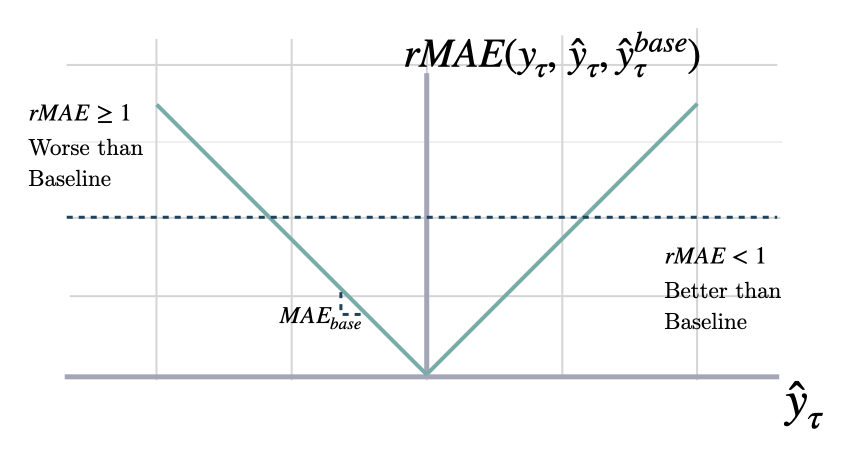
*RMAE Calculates Relative Mean Absolute Error (RMAE) between two sets of forecasts (from two different forecasting methods). A number smaller than one implies that the forecast in the numerator is better than the forecast in the denominator. rMAE(yτ,y^τ,y^τbase)=1H∑τ=t+1t+H∣yτ−y^τ∣MAE(yτ,y^τbase)\mathrm{rMAE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}_{\tau}, \mathbf{\hat{y}}^{base}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \frac{|y_{\tau}-\hat{y}_{\tau}|}{\mathrm{MAE}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{base}_{\tau})} Parameters:
y: numpy array, observed values.
y_hat1: numpy array. Predicted values of first model.
y_hat2: numpy array. Predicted values of baseline model.
weights: numpy array, optional. Weights for weighted average.
axis: None or int, optional.Axis or axes along which to average a.
The default, axis=None, will average over all of the elements of the input array. Returns:
rmae: numpy array or double. References:
Rob J. Hyndman, & Koehler, A. B. “Another look at measures of forecast accuracy”.*

​
4. Probabilistic Errors

These measure absolute deviation non-symmetrically, that produce under/over estimation.

​
Quantile Loss

source

​
quantile_loss

 quantile_loss (y:numpy.ndarray, y_hat:numpy.ndarray, q:float=0.5,
                weights:Optional[numpy.ndarray]=None,
                axis:Optional[int]=None)
*Quantile Loss Computes the quantile loss between y and y_hat. QL measures the deviation of a quantile forecast. By weighting the absolute deviation in a non symmetric way, the loss pays more attention to under or over estimation. A common value for q is 0.5 for the deviation from the median (Pinball loss). QL(yτ,y^τ(q))=1H∑τ=t+1t+H((1−q) (y^τ(q)−yτ)++q (yτ−y^τ(q))+)\mathrm{QL}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q)}_{\tau}) = \frac{1}{H} \sum^{t+H}_{\tau=t+1} \Big( (1-q)\,( \hat{y}^{(q)}_{\tau} - y_{\tau} )_{+} + q\,( y_{\tau} - \hat{y}^{(q)}_{\tau} )_{+} \Big) Parameters:
y: numpy array, Actual values.
y_hat: numpy array, Predicted values.
q: float, between 0 and 1. The slope of the quantile loss, in the context of quantile regression, the q determines the conditional quantile level.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
quantile_loss: numpy array, (single value). References:
Roger Koenker and Gilbert Bassett, Jr., “Regression Quantiles”.*

​
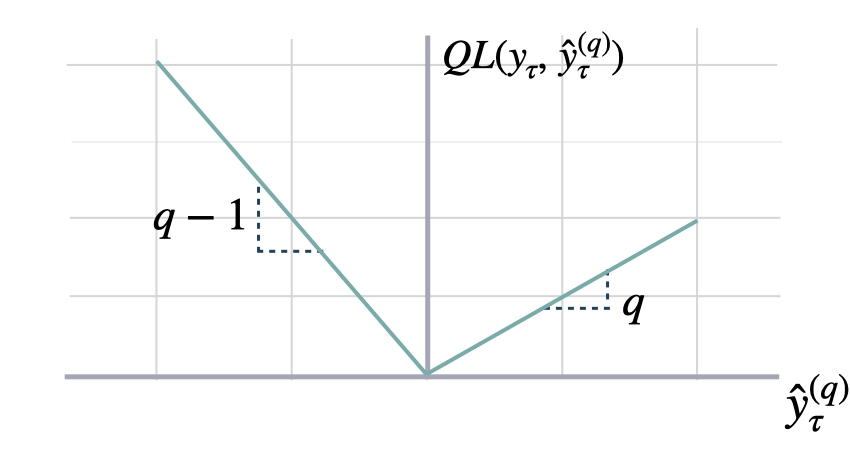
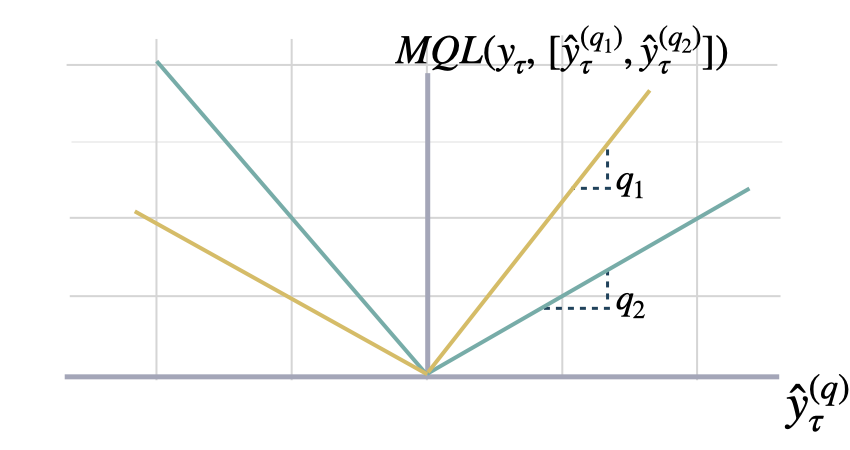
Multi-Quantile Loss

source

​
mqloss

 mqloss (y:numpy.ndarray, y_hat:numpy.ndarray, quantiles:numpy.ndarray,
         weights:Optional[numpy.ndarray]=None, axis:Optional[int]=None)
*Multi-Quantile loss Calculates the Multi-Quantile loss (MQL) between y and y_hat. MQL calculates the average multi-quantile Loss for a given set of quantiles, based on the absolute difference between predicted quantiles and observed values. MQL(yτ,[y^τ(q1),...,y^τ(qn)])=1n∑qiQL(yτ,y^τ(qi))\mathrm{MQL}(\mathbf{y}_{\tau},[\mathbf{\hat{y}}^{(q_{1})}_{\tau}, ... ,\hat{y}^{(q_{n})}_{\tau}]) = \frac{1}{n} \sum_{q_{i}} \mathrm{QL}(\mathbf{y}_{\tau}, \mathbf{\hat{y}}^{(q_{i})}_{\tau}) The limit behavior of MQL allows to measure the accuracy of a full predictive distribution F^τ\mathbf{\hat{F}}_{\tau} with the continuous ranked probability score (CRPS). This can be achieved through a numerical integration technique, that discretizes the quantiles and treats the CRPS integral with a left Riemann approximation, averaging over uniformly distanced quantiles. CRPS(yτ,F^τ)=∫01QL(yτ,y^τ(q))dq\mathrm{CRPS}(y_{\tau}, \mathbf{\hat{F}}_{\tau}) = \int^{1}_{0} \mathrm{QL}(y_{\tau}, \hat{y}^{(q)}_{\tau}) dq Parameters:
y: numpy array, Actual values.
y_hat: numpy array, Predicted values.
quantiles: numpy array,(n_quantiles). Quantiles to estimate from the distribution of y.
mask: numpy array, Specifies date stamps per serie to consider in loss.
 Returns:
mqloss: numpy array, (single value). References:
Roger Koenker and Gilbert Bassett, Jr., “Regression Quantiles”.
James E. Matheson and Robert L. Winkler, “Scoring Rules for Continuous Probability Distributions”.*

​
Examples and Validation

import unittest
import torch as t 
import numpy as np

from neuralforecast.losses.pytorch import (
    MAE, MSE, RMSE,      # unscaled errors
    MAPE, SMAPE,         # percentage errors
    MASE,                # scaled error
    QuantileLoss, MQLoss # probabilistic errors
)

from neuralforecast.losses.numpy import (
    mae, mse, rmse,              # unscaled errors
    mape, smape,                 # percentage errors
    mase,                        # scaled error
    quantile_loss, mqloss        # probabilistic errors
)