Skip to main content

​
Introduction

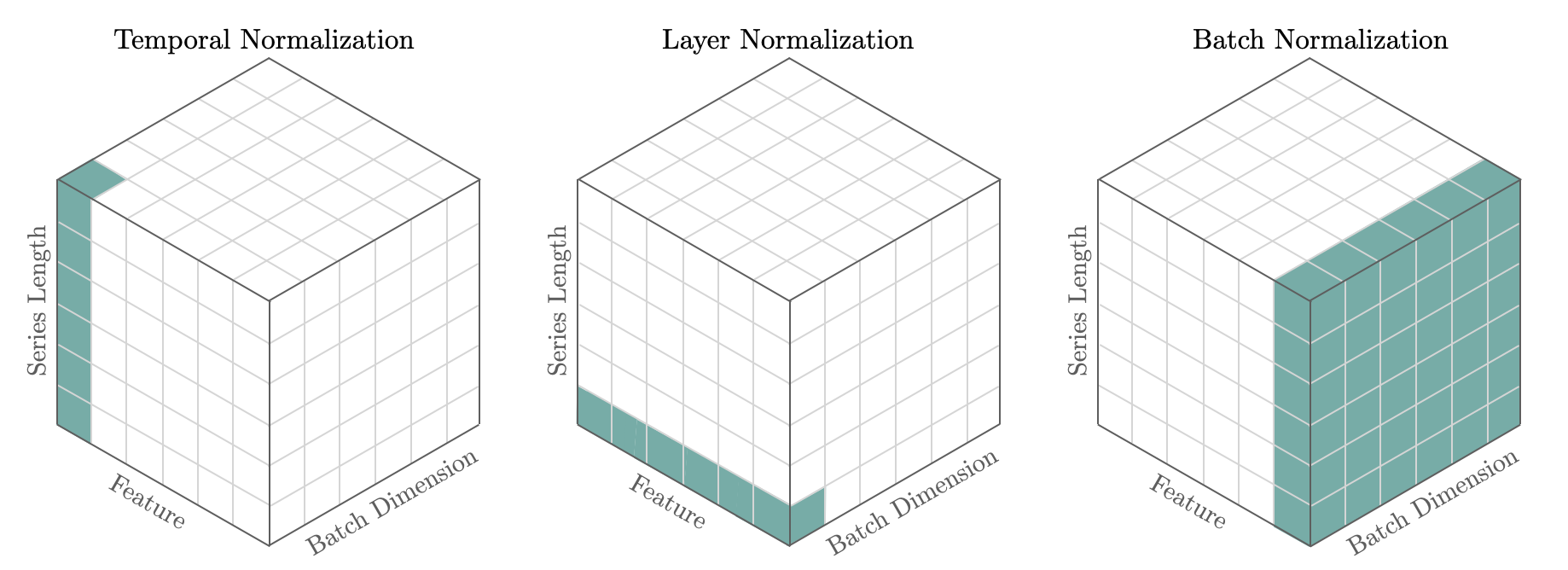
Temporal normalization has proven to be essential in neural forecasting tasks, as it enables network’s non-linearities to express themselves. Forecasting scaling methods take particular interest in the temporal dimension where most of the variance dwells, contrary to other deep learning techniques like BatchNorm that normalizes across batch and temporal dimensions, and LayerNorm that normalizes across the feature dimension. Currently we support the following techniques: std, median, norm, norm1, invariant, revin.

​
References

Figure 1. Illustration of temporal normalization (left), layer normalization (center) and batch normalization (right). The entries in green show the components used to compute the normalizing statistics.

​
1. Auxiliary Functions

​
masked_median

masked_median(x, mask, dim=-1, keepdim=True)
Masked Median Compute the median of tensor x along dim, ignoring values where mask is False. x and mask need to be broadcastable. Parameters:
NameTypeDescriptionDefault
xTensorTensor to compute median of along dim dimension.required
maskTensorTensor bool with same shape as x, where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
dimintDimension to take median of. Defaults to -1.-1
keepdimboolKeep dimension of x or not. Defaults to True.True
Returns:
TypeDescription
torch.Tensor: Normalized values.

​
masked_mean

masked_mean(x, mask, dim=-1, keepdim=True)
Masked Mean Compute the mean of tensor x along dimension, ignoring values where mask is False. x and mask need to be broadcastable. Parameters:
NameTypeDescriptionDefault
xTensorTensor to compute mean of along dim dimension.required
maskTensorTensor bool with same shape as x, where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
dimintDimension to take mean of. Defaults to -1.-1
keepdimboolKeep dimension of x or not. Defaults to True.True
Returns:
TypeDescription
torch.Tensor: Normalized values.

​
2. Scalers

​
minmax_statistics

minmax_statistics(x, mask, eps=1e-06, dim=-1)
MinMax Scaler Standardizes temporal features by ensuring its range dweels between [0,1] range. This transformation is often used as an alternative to the standard scaler. The scaled features are obtained as: z=(x[B,T,C]−min(x)[B,1,C])/(max(x)[B,1,C]−min(x)[B,1,C])\mathbf{z} = (\mathbf{x}_{[B,T,C]}-\mathrm{min}({\mathbf{x}})_{[B,1,C]})/ (\mathrm{max}({\mathbf{x}})_{[B,1,C]}- \mathrm{min}({\mathbf{x}})_{[B,1,C]}) Parameters:
NameTypeDescriptionDefault
xTensorInput tensor.required
maskTensorTensor bool, same dimension as x, indicates where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
epsfloatSmall value to avoid division by zero. Defaults to 1e-6.1e-06
dimintDimension over to compute min and max. Defaults to -1.-1
Returns:
TypeDescription
torch.Tensor: Same shape as x, except scaled.

​
minmax1_statistics

minmax1_statistics(x, mask, eps=1e-06, dim=-1)
MinMax1 Scaler Standardizes temporal features by ensuring its range dweels between [-1,1] range. This transformation is often used as an alternative to the standard scaler or classic Min Max Scaler. The scaled features are obtained as: z=2(x[B,T,C]−min(x)[B,1,C])/(max(x)[B,1,C]−min(x)[B,1,C])−1\mathbf{z} = 2 (\mathbf{x}_{[B,T,C]}-\mathrm{min}({\mathbf{x}})_{[B,1,C]})/ (\mathrm{max}({\mathbf{x}})_{[B,1,C]}- \mathrm{min}({\mathbf{x}})_{[B,1,C]})-1 Parameters:
NameTypeDescriptionDefault
xTensorInput tensor.required
maskTensorTensor bool, same dimension as x, indicates where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
epsfloatSmall value to avoid division by zero. Defaults to 1e-6.1e-06
dimintDimension over to compute min and max. Defaults to -1.-1
Returns:
TypeDescription
torch.Tensor: Same shape as x, except scaled.

​
std_statistics

std_statistics(x, mask, dim=-1, eps=1e-06)
Standard Scaler Standardizes features by removing the mean and scaling to unit variance along the dim dimension. For example, for base_windows models, the scaled features are obtained as (with dim=1): z=(x[B,T,C]−xˉ[B,1,C])/σ^[B,1,C]\mathbf{z} = (\mathbf{x}_{[B,T,C]}-\bar{\mathbf{x}}_{[B,1,C]})/\hat{\sigma}_{[B,1,C]} Parameters:
NameTypeDescriptionDefault
xTensorInput tensor.required
maskTensorTensor bool, same dimension as x, indicates where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
epsfloatSmall value to avoid division by zero. Defaults to 1e-6.1e-06
dimintDimension over to compute mean and std. Defaults to -1.-1
Returns:
TypeDescription
torch.Tensor: Same shape as x, except scaled.

​
robust_statistics

robust_statistics(x, mask, dim=-1, eps=1e-06)
Robust Median Scaler Standardizes features by removing the median and scaling with the mean absolute deviation (mad) a robust estimator of variance. This scaler is particularly useful with noisy data where outliers can heavily influence the sample mean / variance in a negative way. In these scenarios the median and amd give better results. For example, for base_windows models, the scaled features are obtained as (with dim=1): z=(x[B,T,C]−median(x)[B,1,C])/mad(x)[B,1,C]\mathbf{z} = (\mathbf{x}_{[B,T,C]}-\textrm{median}(\mathbf{x})_{[B,1,C]})/\textrm{mad}(\mathbf{x})_{[B,1,C]} mad(x)=1N∑∣x−median(x)∣\textrm{mad}(\mathbf{x}) = \frac{1}{N} \sum_{}|\mathbf{x} - \mathrm{median}(x)| Parameters:
NameTypeDescriptionDefault
xTensorInput tensor.required
maskTensorTensor bool, same dimension as x, indicates where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
epsfloatSmall value to avoid division by zero. Defaults to 1e-6.1e-06
dimintDimension over to compute median and mad. Defaults to -1.-1
Returns:
TypeDescription
torch.Tensor: Same shape as x, except scaled.

​
invariant_statistics

invariant_statistics(x, mask, dim=-1, eps=1e-06)
Invariant Median Scaler Standardizes features by removing the median and scaling with the mean absolute deviation (mad) a robust estimator of variance. Aditionally it complements the transformation with the arcsinh transformation. For example, for base_windows models, the scaled features are obtained as (with dim=1): z=(x[B,T,C]−median(x)[B,1,C])/mad(x)[B,1,C]\mathbf{z} = (\mathbf{x}_{[B,T,C]}-\textrm{median}(\mathbf{x})_{[B,1,C]})/\textrm{mad}(\mathbf{x})_{[B,1,C]} z=arcsinh(z)\mathbf{z} = \textrm{arcsinh}(\mathbf{z}) Parameters:
NameTypeDescriptionDefault
xTensorInput tensor.required
maskTensorTensor bool, same dimension as x, indicates where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
epsfloatSmall value to avoid division by zero. Defaults to 1e-6.1e-06
dimintDimension over to compute median and mad. Defaults to -1.-1
Returns:
TypeDescription
torch.Tensor: Same shape as x, except scaled.

​
identity_statistics

identity_statistics(x, mask, dim=-1, eps=1e-06)
Identity Scaler A placeholder identity scaler, that is argument insensitive. Parameters:
NameTypeDescriptionDefault
xTensorInput tensor.required
maskTensorTensor bool, same dimension as x, indicates where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
epsfloatSmall value to avoid division by zero. Defaults to 1e-6.1e-06
dimintDimension over to compute median and mad. Defaults to -1.-1
Returns:
TypeDescription
torch.Tensor: Original x.

​
3. TemporalNorm Module

​
TemporalNorm

TemporalNorm(scaler_type='robust', dim=-1, eps=1e-06, num_features=None)
Bases: Module Temporal Normalization Standardization of the features is a common requirement for many machine learning estimators, and it is commonly achieved by removing the level and scaling its variance. The TemporalNorm module applies temporal normalization over the batch of inputs as defined by the type of scaler. z[B,T,C]=Scaler(x[B,T,C])\mathbf{z}_{[B,T,C]} = \textrm{Scaler}(\mathbf{x}_{[B,T,C]}) If scaler_type is revin learnable normalization parameters are added on top of the usual normalization technique, the parameters are learned through scale decouple global skip connections. The technique is available for point and probabilistic outputs. z^[B,T,C]=γ^[1,1,C]z[B,T,C]+β^[1,1,C]\mathbf{\hat{z}}_{[B,T,C]} = \boldsymbol{\hat{\gamma}}_{[1,1,C]} \mathbf{z}_{[B,T,C]} +\boldsymbol{\hat{\beta}}_{[1,1,C]} Parameters:
NameTypeDescriptionDefault
scaler_typestrDefines the type of scaler used by TemporalNorm. Available [identity, standard, robust, minmax, minmax1, invariant, revin]. Defaults to “robust”.‘robust’
dim (int, optional): Dimension over to compute scale and shift. Defaults to -1. eps (float, optional): Small value to avoid division by zero. Defaults to 1e-6. num_features (int, optional): For RevIN-like learnable affine parameters initialization. Defaults to None.

​
TemporalNorm.transform

transform(x, mask)
Center and scale the data. Parameters:
NameTypeDescriptionDefault
xTensorTensor shape [batch, time, channels].required
maskTensorTensor bool, shape [batch, time] where x is valid and False where x should be masked. Mask should not be all False in any column of dimension dim to avoid NaNs from zero division.required
Returns:
TypeDescription
torch.Tensor: Same shape as x, except scaled.

​
TemporalNorm.inverse_transform

inverse_transform(z, x_shift=None, x_scale=None)
Scale back the data to the original representation. Parameters:
NameTypeDescriptionDefault
zTensorTensor shape [batch, time, channels], scaled.required
x_shiftTensorTensor shape [1, 1, channels], shift. Defaults to None.None
x_scaleTensorTensor shape [1, 1, channels], scale. Defaults to None.None
Returns:
TypeDescription
torch.Tensor: Original data.

​
Example

import numpy as np

# Declare synthetic batch to normalize
x1 = 10**0 * np.arange(36)[:, None]
x2 = 10**1 * np.arange(36)[:, None]

np_x = np.concatenate([x1, x2], axis=1)
np_x = np.repeat(np_x[None, :,:], repeats=2, axis=0)
np_x[0,:,:] = np_x[0,:,:] + 100

np_mask = np.ones(np_x.shape)
np_mask[:, -12:, :] = 0

print(f'x.shape [batch, time, features]={np_x.shape}')
print(f'mask.shape [batch, time, features]={np_mask.shape}')

# Validate scalers
x = 1.0*torch.tensor(np_x)
mask = torch.tensor(np_mask)
scaler = TemporalNorm(scaler_type='standard', dim=1)
x_scaled = scaler.transform(x=x, mask=mask)
x_recovered = scaler.inverse_transform(x_scaled)

plt.plot(x[0,:,0], label='x1', color='#78ACA8')
plt.plot(x[0,:,1], label='x2',  color='#E3A39A')
plt.title('Before TemporalNorm')
plt.xlabel('Time')
plt.legend()
plt.show()

plt.plot(x_scaled[0,:,0], label='x1', color='#78ACA8')
plt.plot(x_scaled[0,:,1]+0.1, label='x2+0.1', color='#E3A39A')
plt.title(f'TemporalNorm \'{scaler.scaler_type}\' ')
plt.xlabel('Time')
plt.legend()
plt.show()

plt.plot(x_recovered[0,:,0], label='x1', color='#78ACA8')
plt.plot(x_recovered[0,:,1], label='x2', color='#E3A39A')
plt.title('Recovered')
plt.xlabel('Time')
plt.legend()
plt.show()