Skip to main content

Documentation Index

Fetch the complete documentation index at: https://nixtlaverse.nixtla.io/llms.txt

Use this file to discover all available pages before exploring further.

In this example we will show how to perform electricity load forecasting using MLForecast alongside many models. We also compare them against the prophet library.

​
Introduction

Some time series are generated from very low frequency data. These data generally exhibit multiple seasonalities. For example, hourly data may exhibit repeated patterns every hour (every 24 observations) or every day (every 24 * 7, hours per day, observations). This is the case for electricity load. Electricity load may vary hourly, e.g., during the evenings electricity consumption may be expected to increase. But also, the electricity load varies by week. Perhaps on weekends there is an increase in electrical activity. In this example we will show how to model the two seasonalities of the time series to generate accurate forecasts in a short time. We will use hourly PJM electricity load data. The original data can be found here.

​
Libraries

In this example we will use the following libraries:
  • mlforecast. Accurate and ⚡️ fast forecasting with classical machine learning models.
  • prophet. Benchmark model developed by Facebook.
  • utilsforecast. Library with different functions for forecasting evaluation.
If you have already installed the libraries you can skip the next cell, if not be sure to run it. 
# %%capture
# !pip install prophet
# !pip install -U mlforecast
# !pip install -U utilsforecast

​
Forecast using Multiple Seasonalities

​
Electricity Load Data

According to the dataset’s page,
PJM Interconnection LLC (PJM) is a regional transmission organization (RTO) in the United States. It is part of the Eastern Interconnection grid operating an electric transmission system serving all or parts of Delaware, Illinois, Indiana, Kentucky, Maryland, Michigan, New Jersey, North Carolina, Ohio, Pennsylvania, Tennessee, Virginia, West Virginia, and the District of Columbia. The hourly power consumption data comes from PJM’s website and are in megawatts (MW).
Let’s take a look to the data. 
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from utilsforecast.plotting import plot_series

pd.plotting.register_matplotlib_converters()
plt.rc("figure", figsize=(10, 8))
plt.rc("font", size=10)

data_url = 'https://raw.githubusercontent.com/panambY/Hourly_Energy_Consumption/master/data/PJM_Load_hourly.csv'
df = pd.read_csv(data_url, parse_dates=['Datetime'])
df.columns = ['ds', 'y']
df.insert(0, 'unique_id', 'PJM_Load_hourly')
df['ds'] = pd.to_datetime(df['ds'])
df = df.sort_values(['unique_id', 'ds']).reset_index(drop=True)
print(f'Shape of the data {df.shape}')
df.tail()

Shape of the data (32896, 3)
unique_iddsy
32891PJM_Load_hourly2001-12-31 20:00:0036392.0
32892PJM_Load_hourly2001-12-31 21:00:0035082.0
32893PJM_Load_hourly2001-12-31 22:00:0033890.0
32894PJM_Load_hourly2001-12-31 23:00:0032590.0
32895PJM_Load_hourly2002-01-01 00:00:0031569.0
fig = plot_series(df)
We clearly observe that the time series exhibits seasonal patterns. Moreover, the time series contains 32,896 observations, so it is necessary to use very computationally efficient methods to display them in production. We are going to split our series in order to create a train and test set. The model will be tested using the last 24 hours of the timeseries. 
threshold_time = df['ds'].max() - pd.Timedelta(hours=24)

# Split the dataframe
df_train = df[df['ds'] <= threshold_time]
df_last_24_hours = df[df['ds'] > threshold_time]

​
Analizing Seasonalities

First we must visualize the seasonalities of the model. As mentioned before, the electricity load presents seasonalities every 24 hours (Hourly) and every 24 * 7 (Daily) hours. Therefore, we will use [24, 24 * 7] as the seasonalities for the model. In order to analize how they affect our series we are going to use the Difference method. 
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
We can use the MLForecast.preprocess method to explore different transformations. It looks like these series have a strong seasonality on the hour of the day, so we can subtract the value from the same hour in the previous day to remove it. This can be done with the mlforecast.target_transforms.Differences transformer, which we pass through target_transforms. In order to analize the trends individually and combined we are going to plot them individually and combined. Therefore, we can compare them against the original series. We can use the next function for that. 
def plot_differences(df, differences,fname):
    prep = [df]
    # Plot individual Differences
    for d in differences:
        fcst = MLForecast(
        models=[],  # we're not interested in modeling yet
        freq='H',  # our series have hourly frequency
        target_transforms=[Differences([d])],
        )
        df_ = fcst.preprocess(df)
        df_['unique_id'] = df_['unique_id'] + f'_{d}'
        prep.append(df_)

    # Plot combined Differences
    fcst = MLForecast(
    models=[],  # we're not interested in modeling yet
    freq='H',  # our series have hourly frequency
    target_transforms=[Differences([24, 24*7])],
    )
    df_ = fcst.preprocess(df)
    df_['unique_id'] = df_['unique_id'] + f'_all_diff'
    prep.append(df_)
    prep = pd.concat(prep, ignore_index=True)
    #return prep
    n_series = len(prep['unique_id'].unique())
    fig, ax = plt.subplots(nrows=n_series, figsize=(7 * n_series, 10*n_series), squeeze=False)
    for title, axi in zip(prep['unique_id'].unique(), ax.flat):
        df_ = prep[prep['unique_id'] == title]
        df_.set_index('ds')['y'].plot(title=title, ax=axi)
    fig.savefig(f'../../figs/{fname}', bbox_inches='tight')
    plt.close()
Since the seasonalities are present at 24 hours (daily) and 24*7 (weekly) we are going to subtract them from the serie using Differences([24, 24*7]) and plot them. 
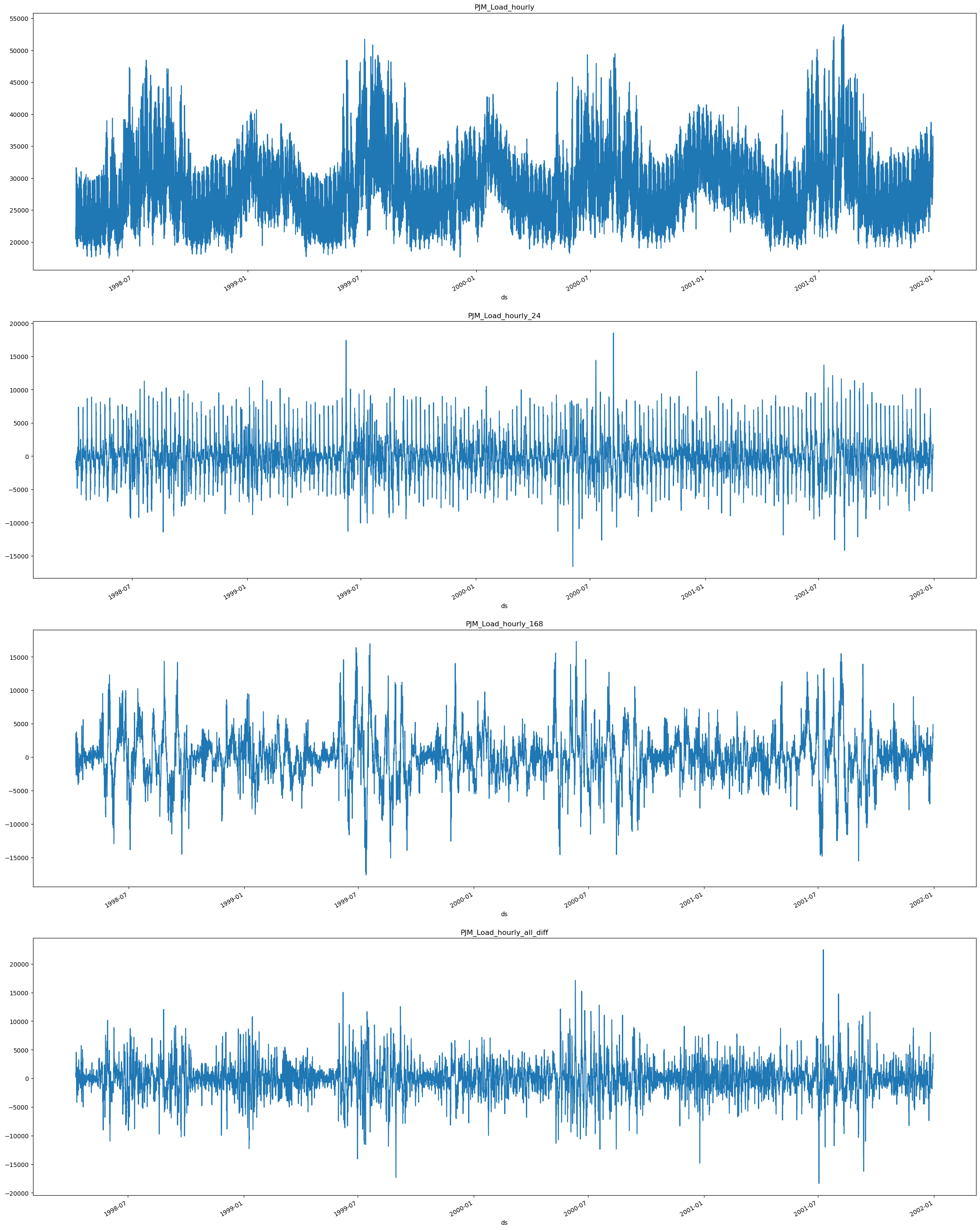
plot_differences(df=df_train, differences=[24, 24*7], fname='load_forecasting__differences.png')
As we can see when we extract the 24 difference (daily) in PJM_Load_hourly_24 the series seem to stabilize since the peaks seem more uniform in comparison with the original series PJM_Load_hourly. When we extract the 24*7 (weekly) PJM_Load_hourly_168 difference we can see there is more periodicity in the peaks in comparison with the original series. Finally we can see the result from the combined result from subtracting all the differences PJM_Load_hourly_all_diff. For modeling we are going to use both difference for the forecasting, therefore we are setting the argument target_transforms from the MLForecast object equal to [Differences([24, 24*7])], if we wanted to include a yearly difference we would need to add the term 24*365. 
fcst = MLForecast(
    models=[],  # we're not interested in modeling yet
    freq='H',  # our series have hourly frequency
    target_transforms=[Differences([24, 24*7])],
)
prep = fcst.preprocess(df_train)
prep
unique_iddsy
192PJM_Load_hourly1998-04-09 02:00:00831.0
193PJM_Load_hourly1998-04-09 03:00:00918.0
194PJM_Load_hourly1998-04-09 04:00:00760.0
195PJM_Load_hourly1998-04-09 05:00:00849.0
196PJM_Load_hourly1998-04-09 06:00:00710.0
…………
32867PJM_Load_hourly2001-12-30 20:00:003417.0
32868PJM_Load_hourly2001-12-30 21:00:003596.0
32869PJM_Load_hourly2001-12-30 22:00:003501.0
32870PJM_Load_hourly2001-12-30 23:00:003939.0
32871PJM_Load_hourly2001-12-31 00:00:004235.0
fig = plot_series(prep)

​
Model Selection with Cross-Validation

We can test many models simultaneously using MLForecast cross_validation. We can import lightgbm and scikit-learn models and try different combinations of them, alongside different target transformations (as the ones we created previously) and historical variables.
You can see an in-depth tutorial on how to use MLForecast Cross Validation methods here 
import lightgbm as lgb
from sklearn.base import BaseEstimator
from sklearn.linear_model import Lasso, LinearRegression, Ridge
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.ensemble import RandomForestRegressor

from mlforecast.lag_transforms import ExpandingMean, RollingMean
from mlforecast.target_transforms import Differences
We can create a benchmark Naive model that uses the electricity load of the last hour as prediction lag1 as showed in the next cell. You can create your own models and try them with MLForecast using the same structure. 
class Naive(BaseEstimator):
    def fit(self, X, y):
        return self

    def predict(self, X):
        return X['lag1']
Now let’s try differen models from the scikit-learn library: Lasso, LinearRegression, Ridge, KNN, MLP and Random Forest alongside the LightGBM. You can add any model to the dictionary to train and compare them by adding them to the dictionary (models) as shown. 
# Model dictionary
models ={
        'naive': Naive(),
        'lgbm': lgb.LGBMRegressor(verbosity=-1),
        'lasso': Lasso(),
        'lin_reg': LinearRegression(),
        'ridge': Ridge(),
        'knn': KNeighborsRegressor(),
        'mlp': MLPRegressor(),
        'rf': RandomForestRegressor()
    }
The we can instanciate the MLForecast class with the models we want to try along side target_transforms, lags, lag_transforms, and date_features. All this features are applied to the models we selected. In this case we use the 1st, 12th and 24th lag, which are passed as a list. Potentially you could pass a range. 
lags=[1,12,24]
Lag transforms are defined as a dictionary where the keys are the lags and the values are lists of the transformations that we want to apply to that lag. You can refer to the lag transformations guide for more details. For using the date features you need to be sure that your time column is made of timestamps. Then it might make sense to extract features like week, dayofweek, quarter, etc. You can do that by passing a list of strings with pandas time/date components. You can also pass functions that will take the time column as input, as we’ll show here.
Here we add month, hour and dayofweek features: 
    date_features=['month', 'hour', 'dayofweek']

mlf = MLForecast(
    models = models,
    freq='H',  # our series have hourly frequency
    target_transforms=[Differences([24, 24*7])],
    lags=[1,12,24], # Lags to be used as features
    lag_transforms={
        1: [ExpandingMean()],
        24: [RollingMean(window_size=48)],
    },
    date_features=['month', 'hour', 'dayofweek']
)
Now we use the cross_validation method to train and evalaute the models. + df: Receives the training data + h: Forecast horizon + n_windows: The number of folds we want to predict You can specify the names of the time series id, time and target columns. + id_col:Column that identifies each serie ( Default unique_id ) + time_col: Column that identifies each timestep, its values can be timestamps or integer( Default ds ) + target_col:Column that contains the target ( Default y ) 
crossvalidation_df = mlf.cross_validation(
    df=df_train,
    h=24,
    n_windows=4,
    refit=False,
)
crossvalidation_df.head()
unique_iddscutoffynaivelgbmlassolin_regridgeknnmlprf
0PJM_Load_hourly2001-12-27 01:00:002001-12-2728332.028837.028526.50557228703.18571228702.62594928702.62595628479.028660.02194727995.17
1PJM_Load_hourly2001-12-27 02:00:002001-12-2727329.027969.027467.86084727693.50231827692.39595427692.39596927521.627584.63543427112.50
2PJM_Load_hourly2001-12-27 03:00:002001-12-2726986.027435.026605.71061526991.79512426990.15756726990.15758926451.626809.41247726529.72
3PJM_Load_hourly2001-12-27 04:00:002001-12-2727009.027401.026284.06513826789.41839926787.26226226787.26229126388.426523.41634826490.83
4PJM_Load_hourly2001-12-27 05:00:002001-12-2727555.028169.026823.61707827369.64378927366.98307527366.98311126779.626986.35599227180.69
Now we can plot each model and window (fold) to see how it behaves 
def plot_cv(df, df_cv, uid, fname, last_n=24 * 14, models={}):
    cutoffs = df_cv.query('unique_id == @uid')['cutoff'].unique()
    fig, ax = plt.subplots(nrows=len(cutoffs), ncols=1, figsize=(14, 14), gridspec_kw=dict(hspace=0.8))
    for cutoff, axi in zip(cutoffs, ax.flat):
        max_date = df_cv.query('unique_id == @uid & cutoff == @cutoff')['ds'].max()
        df[df['ds'] < max_date].query('unique_id == @uid').tail(last_n).set_index('ds').plot(ax=axi, title=uid, y='y')
        for m in models.keys():
            df_cv.query('unique_id == @uid & cutoff == @cutoff').set_index('ds').plot(ax=axi, title=uid, y=m)
    fig.savefig(f'../../figs/{fname}', bbox_inches='tight')
    plt.close()

plot_cv(df_train, crossvalidation_df, 'PJM_Load_hourly', 'load_forecasting__predictions.png', models=models)
Visually examining the forecasts can give us some idea of how the model is behaving, yet in order to asses the performace we need to evaluate them trough metrics. For that we use the utilsforecast library that contains many useful metrics and an evaluate function. 
from utilsforecast.losses import mae, mape, rmse, smape
from utilsforecast.evaluation import evaluate

# Metrics to be used for evaluation
metrics = [
    mae,
    rmse,
    mape,
    smape
]

# Function to evaluate the crossvalidation
def evaluate_crossvalidation(crossvalidation_df, metrics, models):
    evaluations = []
    for c in crossvalidation_df['cutoff'].unique():
        df_cv = crossvalidation_df.query('cutoff == @c')
        evaluation = evaluate(
            df = df_cv,
            metrics=metrics,
            models=list(models.keys())
            )
        evaluations.append(evaluation)
    evaluations = pd.concat(evaluations, ignore_index=True).drop(columns='unique_id')
    evaluations = evaluations.groupby('metric').mean()
    return evaluations.style.background_gradient(cmap='RdYlGn_r', axis=1)


evaluate_crossvalidation(crossvalidation_df, metrics, models)
 naivelgbmlassolin_regridgeknnmlprf
metric        
mae1631.395833971.5362001003.7964331007.9985971007.9985471248.1458331870.5477221017.957813
mape0.0497590.0309660.0317600.0318880.0318880.0387210.0575040.032341
rmse1871.3989191129.7132561148.6161561153.2627191153.2626641451.9643902102.0982381154.647164
smape0.0247860.0158860.0162690.0163380.0163380.0195490.0299170.016563
We can see that the model lgbm has top performance in most metrics followed by the lasso regression. Both models perform way better than the naive.

​
Test Evaluation

Now we are going to evaluate their performance in the test set. We can use both of them for forecasting the test alongside some prediction intervals. For that we can use the PredictionIntervals function in mlforecast.utils.
You can see an in-depth tutorial of Probabilistic Forecasting here 
from mlforecast.utils import PredictionIntervals

models_evaluation ={
        'lgbm': lgb.LGBMRegressor(verbosity=-1),
        'lasso': Lasso(),
    }

mlf_evaluation = MLForecast(
    models = models_evaluation,
    freq='H',  # our series have hourly frequency
    target_transforms=[Differences([24, 24*7])],
    lags=[1,12,24],
    lag_transforms={
        1: [ExpandingMean()],
        24: [RollingMean(window_size=48)],
    },
    date_features=['month', 'hour', 'dayofweek']
)
Now we’re ready to generate the point forecasts and the prediction intervals. To do this, we’ll use the fit method, which takes the following arguments:
  • df: Series data in long format.
  • id_col: Column that identifies each series. In our case, unique_id.
  • time_col: Column that identifies each timestep, its values can be timestamps or integers. In our case, ds.
  • target_col: Column that contains the target. In our case, y.
The PredictionIntervals function is used to compute prediction intervals for the models using Conformal Prediction. The function takes the following arguments: + n_windows: represents the number of cross-validation windows used to calibrate the intervals + h: the forecast horizon 
mlf_evaluation.fit(
    df = df_train,
    prediction_intervals=PredictionIntervals(n_windows=4, h=24)
)

MLForecast(models=[lgbm, lasso], freq=H, lag_features=['lag1', 'lag12', 'lag24', 'expanding_mean_lag1', 'rolling_mean_lag24_window_size48'], date_features=['month', 'hour', 'dayofweek'], num_threads=1)
Now that the model has been trained we are going to forecast the next 24 hours using the predict method so we can compare them to our test data. Additionally, we are going to create prediction intervals at levels [90,95]. 
levels = [90, 95] # Levels for prediction intervals
forecasts = mlf_evaluation.predict(24, level=levels)
forecasts.head()
unique_iddslgbmlassolgbm-lo-95lgbm-lo-90lgbm-hi-90lgbm-hi-95lasso-lo-95lasso-lo-90lasso-hi-90lasso-hi-95
0PJM_Load_hourly2001-12-31 01:00:0028847.57317629124.08597628544.59346428567.60313029127.54322229150.55288828762.75226928772.60427529475.56767729485.419682
1PJM_Load_hourly2001-12-31 02:00:0027862.58919528365.33074927042.31141427128.83988828596.33850328682.86697727528.54895927619.06522429111.59627529202.112539
2PJM_Load_hourly2001-12-31 03:00:0027044.41896027712.16167625596.65989625688.23042628400.60749328492.17802326236.95536926338.08710229086.23625129187.367984
3PJM_Load_hourly2001-12-31 04:00:0026976.10412527661.57273325249.96152725286.02472228666.18352928702.24672425911.13352125959.81571529363.32975029412.011944
4PJM_Load_hourly2001-12-31 05:00:0026694.24623827393.92237025044.22084525051.54883228336.94364428344.27163125751.54789725762.52481529025.31992429036.296843
The predict method returns a DataFrame witht the predictions for each model (lasso and lgbm) along side the prediction tresholds. The high-threshold is indicated by the keyword hi, the low-threshold by the keyword lo, and the level by the number in the column names. 
test = df_last_24_hours.merge(forecasts, how='left', on=['unique_id', 'ds'])
test.head()
unique_iddsylgbmlassolgbm-lo-95lgbm-lo-90lgbm-hi-90lgbm-hi-95lasso-lo-95lasso-lo-90lasso-hi-90lasso-hi-95
0PJM_Load_hourly2001-12-31 01:00:0029001.028847.57317629124.08597628544.59346428567.60313029127.54322229150.55288828762.75226928772.60427529475.56767729485.419682
1PJM_Load_hourly2001-12-31 02:00:0028138.027862.58919528365.33074927042.31141427128.83988828596.33850328682.86697727528.54895927619.06522429111.59627529202.112539
2PJM_Load_hourly2001-12-31 03:00:0027830.027044.41896027712.16167625596.65989625688.23042628400.60749328492.17802326236.95536926338.08710229086.23625129187.367984
3PJM_Load_hourly2001-12-31 04:00:0027874.026976.10412527661.57273325249.96152725286.02472228666.18352928702.24672425911.13352125959.81571529363.32975029412.011944
4PJM_Load_hourly2001-12-31 05:00:0028427.026694.24623827393.92237025044.22084525051.54883228336.94364428344.27163125751.54789725762.52481529025.31992429036.296843
Now we can evaluate the metrics and performance in the test set. 
evaluate(
    df = test,
    metrics=metrics,
    models=list(models_evaluation.keys())
)
unique_idmetriclgbmlasso
0PJM_Load_hourlymae1092.050817899.979743
1PJM_Load_hourlyrmse1340.4227621163.695525
2PJM_Load_hourlymape0.0336000.027688
3PJM_Load_hourlysmape0.0171370.013812
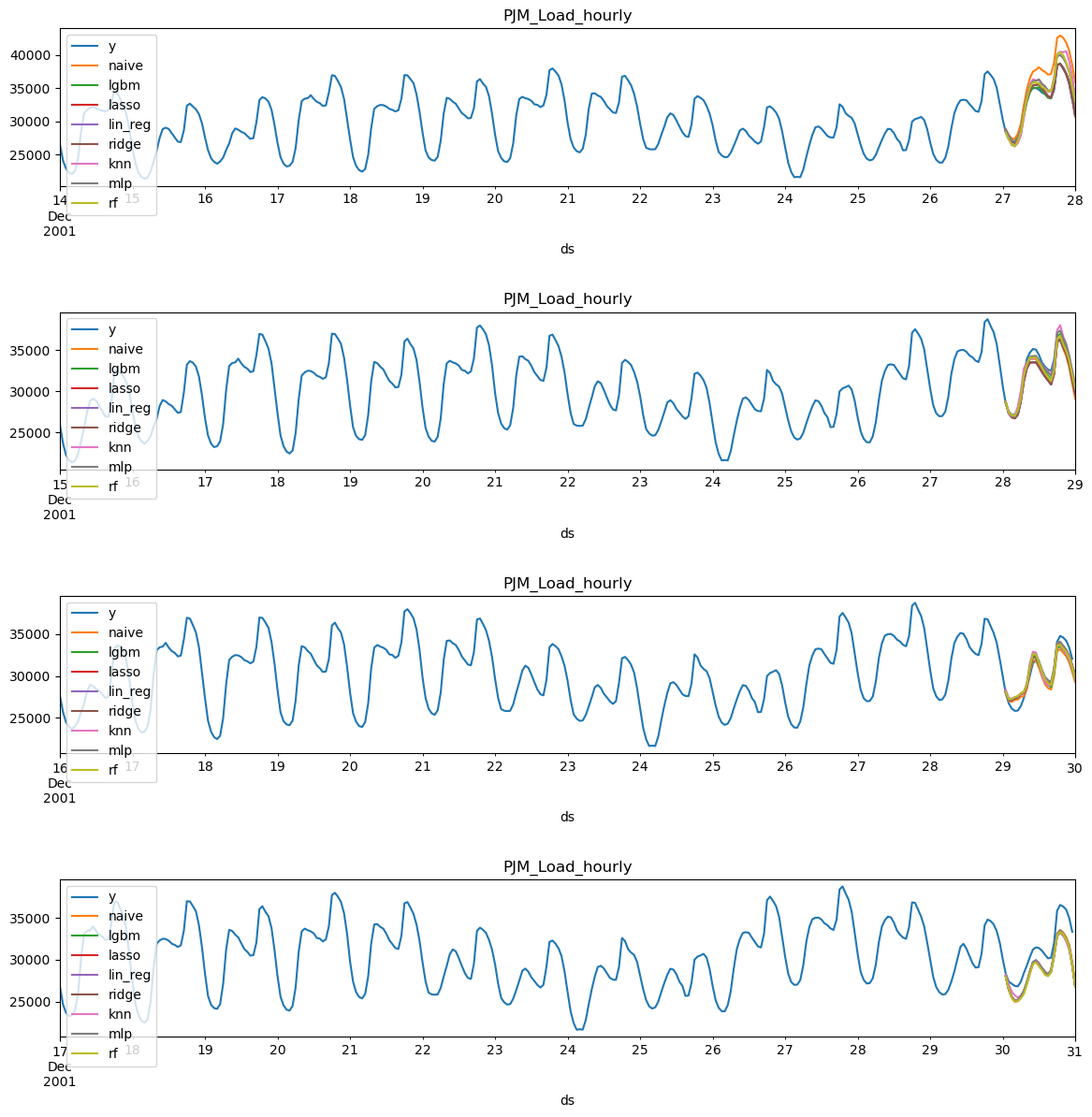
We can see that the lasso regression performed slightly better than the LightGBM for the test set. Additionally, we can also plot the forecasts alongside their prediction intervals. For that we can use the plot_series method available in utilsforecast.plotting. We can plot one or many models at once alongside their confidence intervals. 
fig = plot_series(
    df_train,
    test,
    models=['lasso', 'lgbm'],
    plot_random=False,
    level=levels,
    max_insample_length=24
)

​
Comparison with Prophet

One of the most widely used models for time series forecasting is Prophet. This model is known for its ability to model different seasonalities (weekly, daily yearly). We will use this model as a benchmark to see if the lgbm alongside MLForecast adds value for this time series. 
from prophet import Prophet
from time import time

Importing plotly failed. Interactive plots will not work.

# create prophet model
prophet = Prophet(interval_width=0.9)
init = time()
prophet.fit(df_train)
# produce forecasts
future = prophet.make_future_dataframe(periods=len(df_last_24_hours), freq='H', include_history=False)
forecast_prophet = prophet.predict(future)
end = time()
# data wrangling
forecast_prophet = forecast_prophet[['ds', 'yhat', 'yhat_lower', 'yhat_upper']]
forecast_prophet.columns = ['ds', 'Prophet', 'Prophet-lo-90', 'Prophet-hi-90']
forecast_prophet.insert(0, 'unique_id', 'PJM_Load_hourly')
forecast_prophet.head()
unique_iddsProphetProphet-lo-90Prophet-hi-90
0PJM_Load_hourly2001-12-31 01:00:0025333.44844220589.87355930370.174820
1PJM_Load_hourly2001-12-31 02:00:0024039.92593618927.50348729234.930903
2PJM_Load_hourly2001-12-31 03:00:0023363.99879318428.46251328292.424622
3PJM_Load_hourly2001-12-31 04:00:0023371.79960918206.27344628181.023448
4PJM_Load_hourly2001-12-31 05:00:0024146.46861019356.17149729006.546759
time_prophet = (end - init)
print(f'Prophet Time: {time_prophet:.2f} seconds')

Prophet Time: 18.00 seconds

models_comparison ={
    'lgbm': lgb.LGBMRegressor(verbosity=-1)
}

mlf_comparison = MLForecast(
    models = models_comparison,
    freq='H',  # our series have hourly frequency
    target_transforms=[Differences([24, 24*7])],
    lags=[1,12,24],
    lag_transforms={
        1: [ExpandingMean()],
        24: [RollingMean(window_size=48)],
    },
    date_features=['month', 'hour', 'dayofweek']
)

init = time()
mlf_comparison.fit(
    df = df_train,
    prediction_intervals=PredictionIntervals(n_windows=4, h=24)
)

levels = [90]
forecasts_comparison = mlf_comparison.predict(24, level=levels)
end = time()
forecasts_comparison.head()
unique_iddslgbmlgbm-lo-90lgbm-hi-90
0PJM_Load_hourly2001-12-31 01:00:0028847.57317628567.60313029127.543222
1PJM_Load_hourly2001-12-31 02:00:0027862.58919527128.83988828596.338503
2PJM_Load_hourly2001-12-31 03:00:0027044.41896025688.23042628400.607493
3PJM_Load_hourly2001-12-31 04:00:0026976.10412525286.02472228666.183529
4PJM_Load_hourly2001-12-31 05:00:0026694.24623825051.54883228336.943644
time_lgbm = (end - init)
print(f'LGBM Time: {time_lgbm:.2f} seconds')

LGBM Time: 0.86 seconds

metrics_comparison = df_last_24_hours.merge(forecasts_comparison, how='left', on=['unique_id', 'ds']).merge(
    forecast_prophet, how='left', on=['unique_id', 'ds'])
metrics_comparison = evaluate(
            df = metrics_comparison,
            metrics=metrics,
            models=['Prophet', 'lgbm']
            )
metrics_comparison.reset_index(drop=True).style.background_gradient(cmap='RdYlGn_r', axis=1)
 unique_idmetricProphetlgbm
0PJM_Load_hourlymae2266.5616421092.050817
1PJM_Load_hourlyrmse2701.3027791340.422762
2PJM_Load_hourlymape0.0732260.033600
3PJM_Load_hourlysmape0.0383200.017137
As we can see lgbm had consistently better metrics than prophet. 
metrics_comparison['improvement'] = metrics_comparison['Prophet'] /  metrics_comparison['lgbm']
metrics_comparison['improvement'] = metrics_comparison['improvement'].apply(lambda x: f'{x:.2f}')
metrics_comparison.set_index('metric')[['improvement']]
improvement
metric
mae2.08
rmse2.02
mape2.18
smape2.24
print(f'lgbm with MLForecast has a speedup of {time_prophet/time_lgbm:.2f} compared with prophet')

lgbm with MLForecast has a speedup of 20.95 compared with prophet
We can see that lgbm with MLForecast was able to provide metrics at least twice as good as Prophet as seen in the column improvement above, and way faster.