In many applications, a set of time series is hierarchically organized. Examples include the presence of geographic levels, products, or categories that define different types of aggregations. In such scenarios, forecasters are often required to provide predictions for all disaggregate and aggregate series. A natural desire is for those predictions to be “coherent”, that is, for the bottom series to add up precisely to the forecasts of the aggregated series. In this notebook we present an example on how to use HierarchicalForecast to produce coherent forecasts between temporal levels. We will use the classic Australian Domestic Tourism (Tourism) dataset, which contains monthly time series of the number of visitors to each state of Australia. We will first load the Tourism data and produce base forecasts using an AutoETS model from StatsForecast. Then, we reconciliate the forecasts with several reconciliation algorithms from HierarchicalForecast according to a temporal hierarchy. You can run these experiments using CPU or GPU with Google Colab. Open In Colab 
!pip install hierarchicalforecast statsforecast

​
1. Load and Process Data

In this example we will use the Tourism dataset from the Forecasting: Principles and Practice book. The dataset only contains the time series at the lowest level, so we need to create the time series for all hierarchies. 
import numpy as np
import pandas as pd

Y_df = pd.read_csv('https://raw.githubusercontent.com/Nixtla/transfer-learning-time-series/main/datasets/tourism.csv')
Y_df = Y_df.rename({'Trips': 'y', 'Quarter': 'ds'}, axis=1)
Y_df.insert(0, 'Country', 'Australia')
Y_df = Y_df[['Country', 'Region', 'State', 'Purpose', 'ds', 'y']]
Y_df['ds'] = Y_df['ds'].str.replace(r'(\d+) (Q\d)', r'\1-\2', regex=True)
Y_df['ds'] = pd.PeriodIndex(Y_df["ds"], freq='Q').to_timestamp()
Y_df.head()
CountryRegionStatePurposedsy
0AustraliaAdelaideSouth AustraliaBusiness1998-01-01135.077690
1AustraliaAdelaideSouth AustraliaBusiness1998-04-01109.987316
2AustraliaAdelaideSouth AustraliaBusiness1998-07-01166.034687
3AustraliaAdelaideSouth AustraliaBusiness1998-10-01127.160464
4AustraliaAdelaideSouth AustraliaBusiness1999-01-01137.448533

​
2. Temporal reconciliation

First, we add a unique_id to the data. 
Y_df["unique_id"] = Y_df["Country"] + "/" + Y_df["State"] + "/" + Y_df["Region"] + "/" + Y_df["Purpose"]

​
2a. Split Train/Test sets

We use the final two years (8 quarters) as test set. Consequently, our forecast horizon=8. 
horizon = 8

Y_test_df = Y_df.groupby("unique_id", as_index=False).tail(horizon)
Y_train_df = Y_df.drop(Y_test_df.index)

​
2a. Aggregating the dataset according to temporal hierarchy

We first define the temporal aggregation spec. The spec is a dictionary in which the keys are the name of the aggregation and the value is the amount of bottom-level timesteps that should be aggregated in that aggregation. For example, year consists of 12 months, so we define a key, value pair "yearly":12. We can do something similar for other aggregations that we are interested in. In this example, we choose a temporal aggregation of year, semiannual and quarter. The bottom level timesteps have a quarterly frequency. 
spec_temporal = {"year": 4, "semiannual": 2, "quarter": 1}
We next compute the temporally aggregated train- and test sets using the aggregate_temporal function. Note that we have different aggregation matrices S for the train- and test set, as the test set contains temporal hierarchies that are not included in the train set. 
from hierarchicalforecast.utils import aggregate_temporal

Y_train_df, S_train_df, tags_train = aggregate_temporal(df=Y_train_df, spec=spec_temporal)
Y_test_df, S_test_df, tags_test = aggregate_temporal(df=Y_test_df,  spec=spec_temporal)

tags_train

{'year': array(['year-1', 'year-2', 'year-3', 'year-4', 'year-5', 'year-6',
        'year-7', 'year-8', 'year-9', 'year-10', 'year-11', 'year-12',
        'year-13', 'year-14', 'year-15', 'year-16', 'year-17', 'year-18'],
       dtype=object),
 'semiannual': array(['semiannual-1', 'semiannual-2', 'semiannual-3', 'semiannual-4',
        'semiannual-5', 'semiannual-6', 'semiannual-7', 'semiannual-8',
        'semiannual-9', 'semiannual-10', 'semiannual-11', 'semiannual-12',
        'semiannual-13', 'semiannual-14', 'semiannual-15', 'semiannual-16',
        'semiannual-17', 'semiannual-18', 'semiannual-19', 'semiannual-20',
        'semiannual-21', 'semiannual-22', 'semiannual-23', 'semiannual-24',
        'semiannual-25', 'semiannual-26', 'semiannual-27', 'semiannual-28',
        'semiannual-29', 'semiannual-30', 'semiannual-31', 'semiannual-32',
        'semiannual-33', 'semiannual-34', 'semiannual-35', 'semiannual-36'],
       dtype=object),
 'quarter': array(['quarter-1', 'quarter-2', 'quarter-3', 'quarter-4', 'quarter-5',
        'quarter-6', 'quarter-7', 'quarter-8', 'quarter-9', 'quarter-10',
        'quarter-11', 'quarter-12', 'quarter-13', 'quarter-14',
        'quarter-15', 'quarter-16', 'quarter-17', 'quarter-18',
        'quarter-19', 'quarter-20', 'quarter-21', 'quarter-22',
        'quarter-23', 'quarter-24', 'quarter-25', 'quarter-26',
        'quarter-27', 'quarter-28', 'quarter-29', 'quarter-30',
        'quarter-31', 'quarter-32', 'quarter-33', 'quarter-34',
        'quarter-35', 'quarter-36', 'quarter-37', 'quarter-38',
        'quarter-39', 'quarter-40', 'quarter-41', 'quarter-42',
        'quarter-43', 'quarter-44', 'quarter-45', 'quarter-46',
        'quarter-47', 'quarter-48', 'quarter-49', 'quarter-50',
        'quarter-51', 'quarter-52', 'quarter-53', 'quarter-54',
        'quarter-55', 'quarter-56', 'quarter-57', 'quarter-58',
        'quarter-59', 'quarter-60', 'quarter-61', 'quarter-62',
        'quarter-63', 'quarter-64', 'quarter-65', 'quarter-66',
        'quarter-67', 'quarter-68', 'quarter-69', 'quarter-70',
        'quarter-71', 'quarter-72'], dtype=object)}
Our aggregation matrices aggregate the lowest temporal granularity (quarters) up to years. 
S_train_df.iloc[:5, :5]
temporal_idquarter-1quarter-2quarter-3quarter-4
0year-11.01.01.01.0
1year-20.00.00.00.0
2year-30.00.00.00.0
3year-40.00.00.00.0
4year-50.00.00.00.0
S_test_df.iloc[:5, :5]
temporal_idquarter-1quarter-2quarter-3quarter-4
0year-11.01.01.01.0
1year-20.00.00.00.0
2semiannual-11.01.00.00.0
3semiannual-20.00.01.01.0
4semiannual-30.00.00.00.0
If you don’t have a test set available, as is usually the case when you’re making forecasts, it is necessary to create a future dataframe that holds the correct bottom-level unique_ids and timestamps so that they can be temporally aggregated. We can use the make_future_dataframe helper function for that. 
from hierarchicalforecast.utils import make_future_dataframe

Y_test_df_new = make_future_dataframe(Y_train_df, freq="QS", h=horizon)
Y_test_df_new can be then used in aggregate_temporal to construct the temporally aggregated structures: 
Y_test_df_new, S_test_df_new, tags_test_new = aggregate_temporal(df=Y_test_df_new,  spec=spec_temporal)
And we can verify that we have the same temporally aggregated test set, except that Y_test_df_new doesn’t contain the ground truth values y. 
S_test_df_new
temporal_idquarter-1quarter-2quarter-3quarter-4quarter-5quarter-6quarter-7quarter-8
0year-11.01.01.01.00.00.00.00.0
1year-20.00.00.00.01.01.01.01.0
2semiannual-11.01.00.00.00.00.00.00.0
3semiannual-20.00.01.01.00.00.00.00.0
4semiannual-30.00.00.00.01.01.00.00.0
5semiannual-40.00.00.00.00.00.01.01.0
6quarter-11.00.00.00.00.00.00.00.0
7quarter-20.01.00.00.00.00.00.00.0
8quarter-30.00.01.00.00.00.00.00.0
9quarter-40.00.00.01.00.00.00.00.0
10quarter-50.00.00.00.01.00.00.00.0
11quarter-60.00.00.00.00.01.00.00.0
12quarter-70.00.00.00.00.00.01.00.0
13quarter-80.00.00.00.00.00.00.01.0
Y_test_df
temporal_idunique_iddsy
0year-1Australia/ACT/Canberra/Business2016-10-01754.139245
1year-2Australia/ACT/Canberra/Business2017-10-01809.950839
2year-1Australia/ACT/Canberra/Holiday2016-10-01735.365896
3year-2Australia/ACT/Canberra/Holiday2017-10-01834.717900
4year-1Australia/ACT/Canberra/Other2016-10-01175.239916
……………
4251quarter-4Australia/Western Australia/Experience Perth/V…2016-10-01439.699451
4252quarter-5Australia/Western Australia/Experience Perth/V…2017-01-01356.867038
4253quarter-6Australia/Western Australia/Experience Perth/V…2017-04-01302.296119
4254quarter-7Australia/Western Australia/Experience Perth/V…2017-07-01373.442070
4255quarter-8Australia/Western Australia/Experience Perth/V…2017-10-01455.316702
Y_test_df_new
temporal_idunique_idds
0year-1Australia/ACT/Canberra/Business2016-10-01
1year-2Australia/ACT/Canberra/Business2017-10-01
2year-1Australia/ACT/Canberra/Holiday2016-10-01
3year-2Australia/ACT/Canberra/Holiday2017-10-01
4year-1Australia/ACT/Canberra/Other2016-10-01
…………
4251quarter-4Australia/Western Australia/Experience Perth/V…2016-10-01
4252quarter-5Australia/Western Australia/Experience Perth/V…2017-01-01
4253quarter-6Australia/Western Australia/Experience Perth/V…2017-04-01
4254quarter-7Australia/Western Australia/Experience Perth/V…2017-07-01
4255quarter-8Australia/Western Australia/Experience Perth/V…2017-10-01

​
3b. Computing base forecasts

Now, we need to compute base forecasts for each temporal aggregation. The following cell computes the base forecasts for each temporal aggregation in Y_train_df using the AutoETS model. Observe that Y_hat_df contains the forecasts but they are not coherent. Note also that both frequency and horizon are different for each temporal aggregation. In this example, the lowest level has a quarterly frequency, and a horizon of 8 (constituting 2 years). The year aggregation thus has a yearly frequency with a horizon of 2. It is of course possible to choose a different model for each level in the temporal aggregation - you can be as creative as you like! 
from statsforecast.models import AutoETS
from statsforecast.core import StatsForecast

Y_hat_dfs = []
id_cols = ["unique_id", "temporal_id", "ds", "y"]
# We will train a model for each temporal level
for level, temporal_ids_train in tags_train.items():
    # Filter the data for the level
    Y_level_train = Y_train_df.query("temporal_id in @temporal_ids_train")
    temporal_ids_test = tags_test[level]
    Y_level_test = Y_test_df.query("temporal_id in @temporal_ids_test")
    # For each temporal level we have a different frequency and forecast horizon
    freq_level = pd.infer_freq(Y_level_train["ds"].unique())
    horizon_level = Y_level_test["ds"].nunique()
    # Train a model and create forecasts
    fcst = StatsForecast(models=[AutoETS(model='ZZZ')], freq=freq_level, n_jobs=-1)
    Y_hat_df_level = fcst.forecast(df=Y_level_train[["ds", "unique_id", "y"]], h=horizon_level, level=[80, 90])
    # Add the test set to the forecast
    Y_hat_df_level = Y_hat_df_level.merge(Y_level_test, on=["ds", "unique_id"], how="left")
    # Put cols in the right order (for readability)
    Y_hat_cols = id_cols + [col for col in Y_hat_df_level.columns if col not in id_cols]
    Y_hat_df_level = Y_hat_df_level[Y_hat_cols]
    # Append the forecast to the list
    Y_hat_dfs.append(Y_hat_df_level)

Y_hat_df = pd.concat(Y_hat_dfs, ignore_index=True)

​
3c. Reconcile forecasts

We can use the HierarchicalReconciliation class to reconcile the forecasts. In this example we use BottomUp and MinTrace. Note that we have to set temporal=True in the reconcile function. Note that temporal reconcilation currently isn’t supported for insample reconciliation methods, such as MinTrace(method='mint_shrink'). 
from hierarchicalforecast.methods import BottomUp, MinTrace
from hierarchicalforecast.core import HierarchicalReconciliation

reconcilers = [
    BottomUp(),
    MinTrace(method="ols"),
]
hrec = HierarchicalReconciliation(reconcilers=reconcilers)
Y_rec_df = hrec.reconcile(Y_hat_df=Y_hat_df, 
                          S_df=S_test_df, 
                          tags=tags_test, 
                          temporal=True, 
                          level=[80, 90])

​
4. Evaluation

The HierarchicalForecast package includes the evaluate function to evaluate the different hierarchies. We evaluate the temporally aggregated forecasts across all temporal aggregations. 
from hierarchicalforecast.evaluation import evaluate
from utilsforecast.losses import mae, scaled_crps

evaluation = evaluate(df = Y_rec_df.drop(columns = 'unique_id'),
                      tags = tags_test,
                      metrics = [mae, scaled_crps],
                      level = [80, 90],
                      id_col='temporal_id')

evaluation.columns = ['level', 'metric', 'Base', 'BottomUp', 'MinTrace(ols)']
numeric_cols = evaluation.select_dtypes(include="number").columns
evaluation[numeric_cols] = evaluation[numeric_cols].map('{:.3}'.format).astype(np.float64)

evaluation
levelmetricBaseBottomUpMinTrace(ols)
0yearmae47.000050.800046.7000
1yearscaled_crps0.05620.06200.0666
2semiannualmae29.500030.500029.1000
3semiannualscaled_crps0.06430.06810.0727
4quartermae19.400019.400018.7000
5quarterscaled_crps0.08760.08760.0864
6Overallmae26.200027.100025.7000
7Overallscaled_crps0.07650.07840.0797
MinTrace(ols) is the best overall point method, scoring the lowest mae on the year and semiannual aggregated forecasts as well as the quarter bottom-level aggregated forecasts. However, the Base method is better overall on the probabilistic measure crps, where it scores the lowest, indicating that the uncertainty levels predicted with the Base method are better in this example.

​
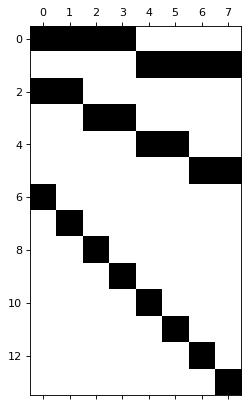
Appendix: plotting the S matrix

from hierarchicalforecast.utils import HierarchicalPlot
We plot our summing matrix for the test set. It’s fairly straightforward: there are two years in the test set, consisting of 4 quarters each. * The first row of the S matrix shows how the aggregation 2016 can be obtained by summing the 4 quarters in 2016. * The second row of the S matrix shows how the aggregation 2017 can be obtained by summing the 4 quarters in 2017. * The next 4 rows show how the semi-annual aggregations can be obtained. * The final rows are the identity matrix for each quarter, denoting the bottom temporal level (each quarter). 
hplot = HierarchicalPlot(S=S_test_df, tags=tags_test, S_id_col="temporal_id")
hplot.plot_summing_matrix()