Skip to main content

Documentation Index

Fetch the complete documentation index at: https://nixtlaverse.nixtla.io/llms.txt

Use this file to discover all available pages before exploring further.

Introduction to Hierarchical Forecasting using HierarchicalForecast
You can run these experiments using CPU or GPU with Google Colab. Open In Colab

​
1. Hierarchical Series

In many applications, a set of time series is hierarchically organized. Examples include the presence of geographic levels, products, or categories that define different types of aggregations. In such scenarios, forecasters are often required to provide predictions for all disaggregate and aggregate series. A natural desire is for those predictions to be β€œcoherent”, that is, for the bottom series to add up precisely to the forecasts of the aggregated series.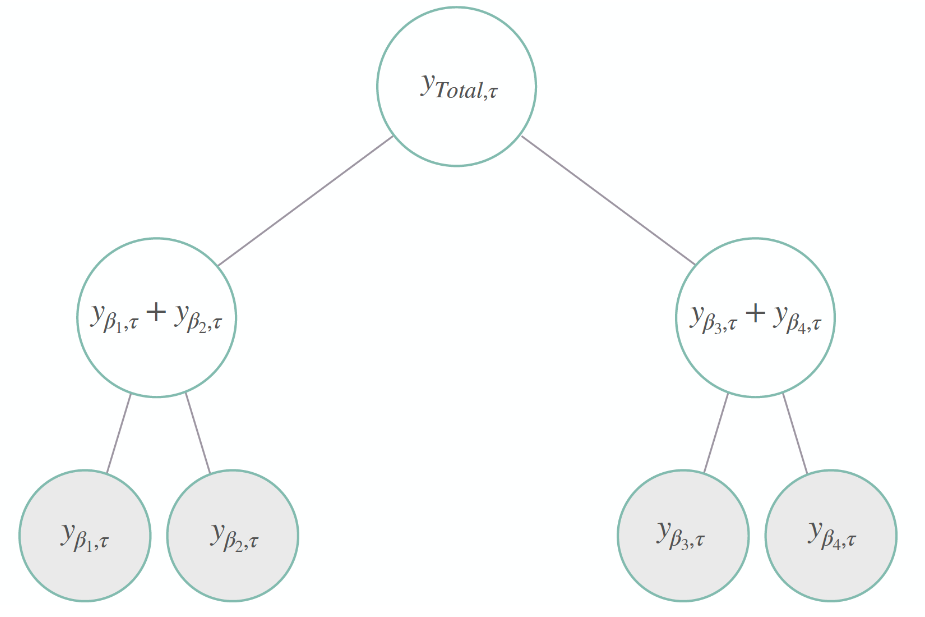 The above figure shows a simple hierarchical structure where we have four bottom-level series, two middle-level series, and the top level representing the total aggregation. Its hierarchical aggregations or coherency constraints are: yTotal,Ο„=yΞ²1,Ο„+yΞ²2,Ο„+yΞ²3,Ο„+yΞ²4,Ο„y[a],Ο„=[yTotal,Ο„,β€…β€ŠyΞ²1,Ο„+yΞ²2,Ο„,β€…β€ŠyΞ²3,Ο„+yΞ²4,Ο„]⊺y[b],Ο„=[yΞ²1,Ο„,β€…β€ŠyΞ²2,Ο„,β€…β€ŠyΞ²3,Ο„,β€…β€ŠyΞ²4,Ο„]⊺y_{\mathrm{Total},\tau} = y_{\beta_{1},\tau}+y_{\beta_{2},\tau}+y_{\beta_{3},\tau}+y_{\beta_{4},\tau} \qquad \qquad \qquad \qquad \qquad \\ \mathbf{y}_{[a],\tau}=\left[y_{\mathrm{Total},\tau},\; y_{\beta_{1},\tau}+y_{\beta_{2},\tau},\;y_{\beta_{3},\tau}+y_{\beta_{4},\tau}\right]^{\intercal} \qquad \mathbf{y}_{[b],\tau}=\left[ y_{\beta_{1},\tau},\; y_{\beta_{2},\tau},\; y_{\beta_{3},\tau},\; y_{\beta_{4},\tau} \right]^{\intercal} Luckily these constraints can be compactly expressed with the following matrices: S[a,b][b]=[A[a][b]I[b][b]]=[1111110000111000010000100001]\mathbf{S}_{[a,b][b]} = \begin{bmatrix} \mathbf{A}_{\mathrm{[a][b]}} \\ \\ \\ \mathbf{I}_{\mathrm{[b][b]}} \\ \\ \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} where A[a,b][b]\mathbf{A}_{[a,b][b]} aggregates the bottom series to the upper levels, and I[b][b]\mathbf{I}_{\mathrm{[b][b]}} is an identity matrix. 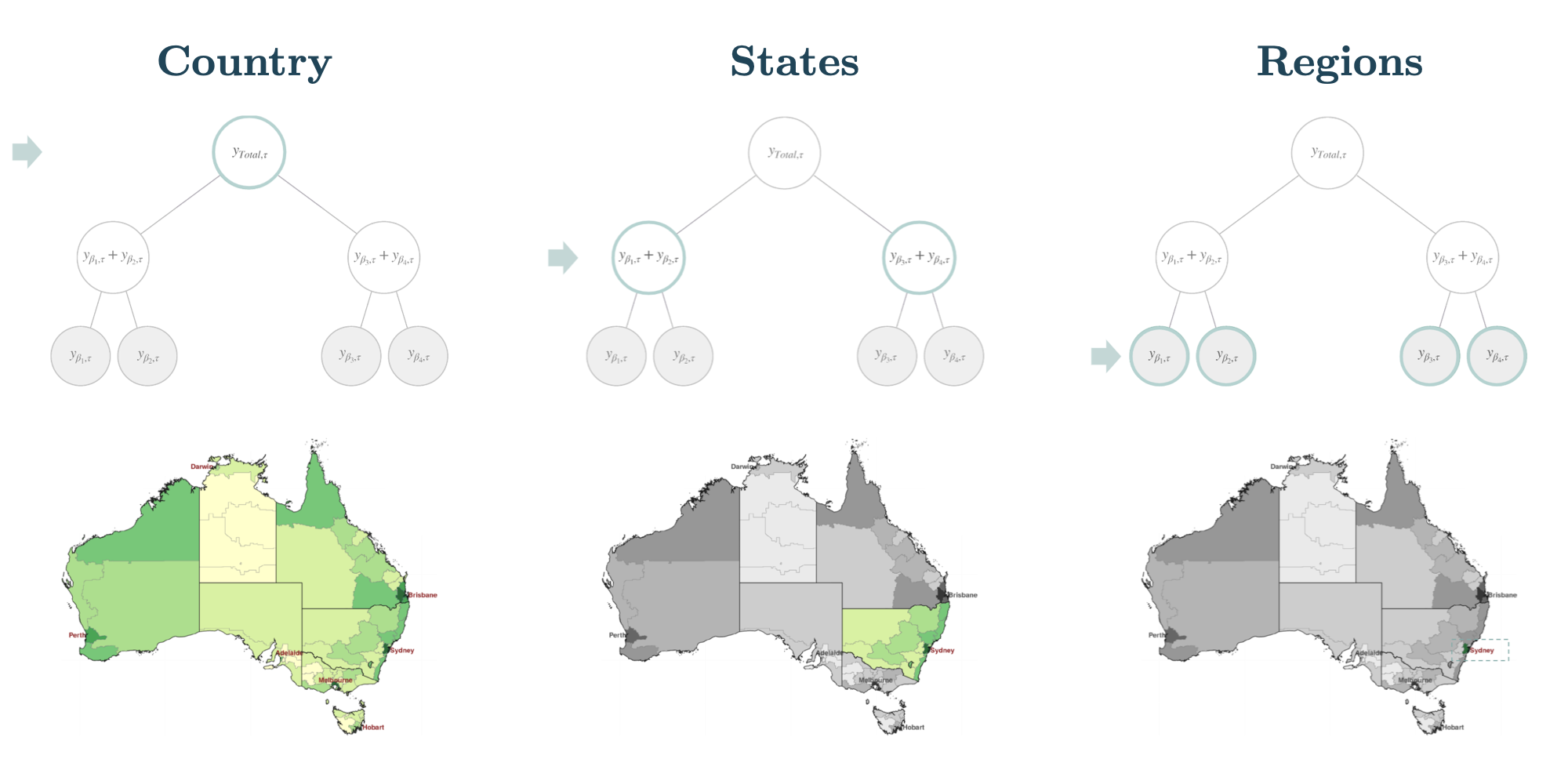The representation of the hierarchical series is then: y[a,b],Ο„=S[a,b][b]y[b],Ο„\mathbf{y}_{[a,b],\tau} = \mathbf{S}_{[a,b][b]} \mathbf{y}_{[b],\tau} To visualize an example, in Figure 2, one can think of the hierarchical time series structure levels to represent different geographical aggregations. For example, in Figure 2, the top level is the total aggregation of series within a country, the middle level being its states and the bottom level its regions.

​
2. Hierarchical Forecast

To achieve β€œcoherency”, most statistical solutions to the hierarchical forecasting challenge implement a two-stage reconciliation process.
  1. First, we obtain a set of the base forecast y^[a,b],Ο„\mathbf{\hat{y}}_{[a,b],\tau}
  2. Later, we reconcile them into coherent forecasts y~[a,b],Ο„\mathbf{\tilde{y}}_{[a,b],\tau}.
Most hierarchical reconciliation methods can be expressed by the following transformations: y~[a,b],Ο„=S[a,b][b]P[b][a,b]y^[a,b],Ο„\tilde{\mathbf{y}}_{[a,b],\tau} = \mathbf{S}_{[a,b][b]} \mathbf{P}_{[b][a,b]} \hat{\mathbf{y}}_{[a,b],\tau} The HierarchicalForecast library offers a Python collection of reconciliation methods, datasets, evaluation and visualization tools for the task. Among its available reconciliation methods we have BottomUp, TopDown, MiddleOut, MinTrace, ERM. Among its probabilistic coherent methods we have Normality, Bootstrap, PERMBU.

​
3. Minimal Example

!pip install hierarchicalforecast statsforecast datasetsforecast

​
Wrangling Data

import numpy as np
import pandas as pd
We are going to create a synthetic data set to illustrate a hierarchical time series structure like the one in Figure 1. We will create a two level structure with four bottom series where aggregations of the series are self evident. 
# Create Figure 1. synthetic bottom data
ds = pd.date_range(start="2000-01-01", end="2000-08-01", freq="MS")
y_base = np.arange(1, 9)
r1 = y_base * (10 ** 1)
r2 = y_base * (10 ** 1)
r3 = y_base * (10 ** 2)
r4 = y_base * (10 ** 2)

ys = np.concatenate([r1, r2, r3, r4])
ds = np.tile(ds, 4)
unique_ids = ["r1"] * 8 + ["r2"] * 8 + ["r3"] * 8 + ["r4"] * 8
top_level = "Australia"
middle_level = ["State1"] * 16 + ["State2"] * 16
bottom_level = unique_ids

bottom_df = dict(
    ds=ds,
    top_level=top_level,
    middle_level=middle_level,
    bottom_level=bottom_level,
    y=ys,
)
bottom_df = pd.DataFrame(bottom_df)
bottom_df.groupby("bottom_level").head(2)
The previously introduced hierarchical series y[a,b]Ο„\mathbf{y}_{[a,b]\tau} is captured within the Y_hier_df dataframe. The aggregation constraints matrix S[a][b]\mathbf{S}_{[a][b]} is captured within the S_df dataframe. Finally tags contains a dictionary of lists within Y_hier_df composing each hierarchical level, for example the tags['top_level'] contains Australia’s aggregated series index. 
from hierarchicalforecast.utils import aggregate

# Create hierarchical structure and constraints
hierarchy_levels = [
    ["top_level"],
    ["top_level", "middle_level"],
    ["top_level", "middle_level", "bottom_level"],
]
Y_hier_df, S_df, tags = aggregate(df=bottom_df, spec=hierarchy_levels)
print("S_df.shape", S_df.shape)
print("Y_hier_df.shape", Y_hier_df.shape)
print("tags['top_level']", tags["top_level"])

Y_hier_df.groupby("unique_id").head(2)

S_df

​
Base Predictions

Next, we compute the base forecast for each time series using the naive model. Observe that Y_hat_df contains the forecasts but they are not coherent. 
from statsforecast.models import Naive
from statsforecast.core import StatsForecast

# Split train/test sets
Y_test_df = Y_hier_df.groupby("unique_id", as_index=False).tail(4)
Y_train_df = Y_hier_df.drop(Y_test_df.index)

# Compute base Naive predictions
# Careful identifying correct data freq, this data monthly 'M'
fcst = StatsForecast(models=[Naive()], freq="MS", n_jobs=-1)
Y_hat_df = fcst.forecast(df=Y_train_df, h=4, fitted=True)
Y_fitted_df = fcst.forecast_fitted_values()

​
Reconciliation

from hierarchicalforecast.methods import BottomUp
from hierarchicalforecast.core import HierarchicalReconciliation

# You can select a reconciler from our collection
reconcilers = [BottomUp()]  # MinTrace(method='mint_shrink')
hrec = HierarchicalReconciliation(reconcilers=reconcilers)

Y_rec_df = hrec.reconcile(Y_hat_df=Y_hat_df, Y_df=Y_fitted_df, S_df=S_df, tags=tags)
Y_rec_df.groupby("unique_id").head(2)

​
References