In many cases, only the time series at the lowest level of the hierarchies (bottom time series) are available. HierarchicalForecast has tools to create time series for all hierarchies and also allows you to calculate prediction intervals for all hierarchies. In this notebook we will see how to do it.

!pip install hierarchicalforecast statsforecast

import pandas as pd

# compute base forecast no coherent
from statsforecast.models import AutoARIMA
from statsforecast.core import StatsForecast

#obtain hierarchical reconciliation methods and evaluation
from hierarchicalforecast.methods import BottomUp, MinTrace
from hierarchicalforecast.utils import aggregate, HierarchicalPlot
from hierarchicalforecast.core import HierarchicalReconciliation

​
Aggregate bottom time series

In this example we will use the Tourism dataset from the Forecasting: Principles and Practice book. The dataset only contains the time series at the lowest level, so we need to create the time series for all hierarchies.

Y_df = pd.read_csv('https://raw.githubusercontent.com/Nixtla/transfer-learning-time-series/main/datasets/tourism.csv')
Y_df = Y_df.rename({'Trips': 'y', 'Quarter': 'ds'}, axis=1)
Y_df.insert(0, 'Country', 'Australia')
Y_df = Y_df[['Country', 'Region', 'State', 'Purpose', 'ds', 'y']]
Y_df['ds'] = Y_df['ds'].str.replace(r'(\d+) (Q\d)', r'\1-\2', regex=True)
Y_df['ds'] = pd.PeriodIndex(Y_df["ds"], freq='Q').to_timestamp()
Y_df.head()
CountryRegionStatePurposedsy
0AustraliaAdelaideSouth AustraliaBusiness1998-01-01135.077690
1AustraliaAdelaideSouth AustraliaBusiness1998-04-01109.987316
2AustraliaAdelaideSouth AustraliaBusiness1998-07-01166.034687
3AustraliaAdelaideSouth AustraliaBusiness1998-10-01127.160464
4AustraliaAdelaideSouth AustraliaBusiness1999-01-01137.448533

The dataset can be grouped in the following non-strictly hierarchical structure.

spec = [
    ['Country'],
    ['Country', 'State'], 
    ['Country', 'Purpose'], 
    ['Country', 'State', 'Region'], 
    ['Country', 'State', 'Purpose'], 
    ['Country', 'State', 'Region', 'Purpose']
]

Using the aggregate function from HierarchicalForecast we can generate: 1. Y_df: the hierarchical structured series y[a,b]τ\mathbf{y}_{[a,b]\tau} 2. S_df: the aggregation constraings dataframe with S[a,b]S_{[a,b]} 3. tags: a list with the ‘unique_ids’ conforming each aggregation level.

Y_df, S_df, tags = aggregate(df=Y_df, spec=spec)

Y_df.head()
unique_iddsy
0Australia1998-01-0123182.197269
1Australia1998-04-0120323.380067
2Australia1998-07-0119826.640511
3Australia1998-10-0120830.129891
4Australia1999-01-0122087.353380
S_df.iloc[:5, :5]
unique_idAustralia/ACT/Canberra/BusinessAustralia/ACT/Canberra/HolidayAustralia/ACT/Canberra/OtherAustralia/ACT/Canberra/Visiting
0Australia1.01.01.01.0
1Australia/ACT1.01.01.01.0
2Australia/New South Wales0.00.00.00.0
3Australia/Northern Territory0.00.00.00.0
4Australia/Queensland0.00.00.00.0
tags['Country/Purpose']

array(['Australia/Business', 'Australia/Holiday', 'Australia/Other',
       'Australia/Visiting'], dtype=object)

We can visualize the S matrix and the data using the HierarchicalPlot class as follows.

hplot = HierarchicalPlot(S=S_df, tags=tags)

hplot.plot_summing_matrix()


hplot.plot_hierarchically_linked_series(
    bottom_series='Australia/ACT/Canberra/Holiday',
    Y_df=Y_df
)

​
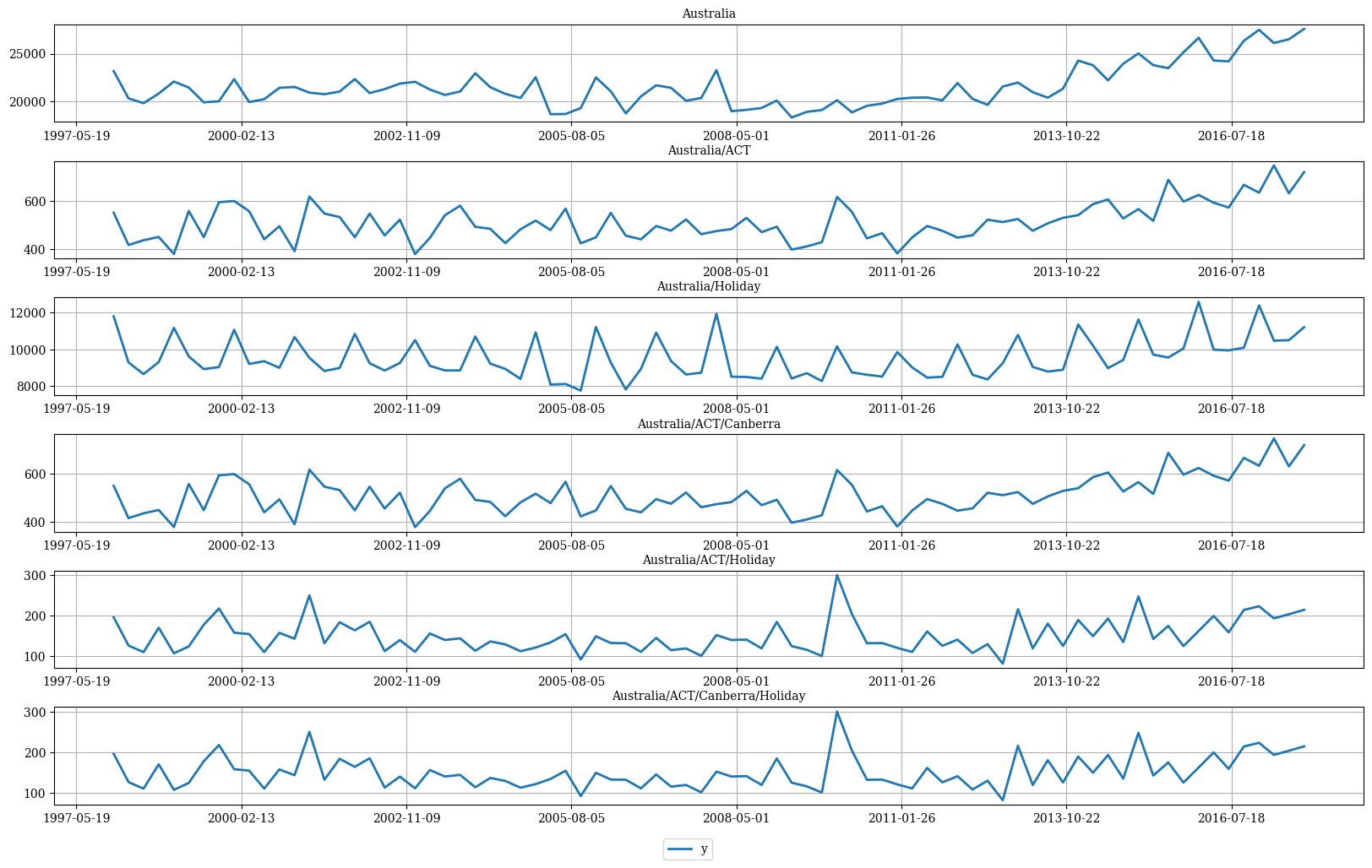
Split Train/Test sets

We use the final two years (8 quarters) as test set.

Y_test_df = Y_df.groupby('unique_id', as_index=False).tail(8)
Y_train_df = Y_df.drop(Y_test_df.index)

Y_train_df.groupby('unique_id').size()

unique_id
Australia                                                72
Australia/ACT                                            72
Australia/ACT/Business                                   72
Australia/ACT/Canberra                                   72
Australia/ACT/Canberra/Business                          72
                                                         ..
Australia/Western Australia/Experience Perth/Other       72
Australia/Western Australia/Experience Perth/Visiting    72
Australia/Western Australia/Holiday                      72
Australia/Western Australia/Other                        72
Australia/Western Australia/Visiting                     72
Length: 425, dtype: int64

​
Computing base forecasts

The following cell computes the base forecasts for each time series in Y_df using the AutoARIMA and model. Observe that Y_hat_df contains the forecasts but they are not coherent. To reconcile the prediction intervals we need to calculate the uncoherent intervals using the level argument of StatsForecast.

fcst = StatsForecast(models=[AutoARIMA(season_length=4)], 
                     freq='QS', n_jobs=-1)
Y_hat_df = fcst.forecast(df=Y_train_df, h=8, fitted=True, level=[80, 90])
Y_fitted_df = fcst.forecast_fitted_values()

​
Reconcile forecasts

The following cell makes the previous forecasts coherent using the HierarchicalReconciliation class. Since the hierarchy structure is not strict, we can’t use methods such as TopDown or MiddleOut. In this example we use BottomUp and MinTrace. If you want to calculate prediction intervals, you have to use the level argument as follows.

reconcilers = [
    BottomUp(),
    MinTrace(method='mint_shrink'),
    MinTrace(method='ols')
]
hrec = HierarchicalReconciliation(reconcilers=reconcilers)
Y_rec_df = hrec.reconcile(Y_hat_df=Y_hat_df, Y_df=Y_fitted_df, 
                          S=S_df, tags=tags, level=[80, 90])

The dataframe Y_rec_df contains the reconciled forecasts.

Y_rec_df.head()
unique_iddsAutoARIMAAutoARIMA-lo-90AutoARIMA-lo-80AutoARIMA-hi-80AutoARIMA-hi-90AutoARIMA/BottomUpAutoARIMA/BottomUp-lo-90AutoARIMA/BottomUp-lo-80…AutoARIMA/MinTrace_method-mint_shrinkAutoARIMA/MinTrace_method-mint_shrink-lo-90AutoARIMA/MinTrace_method-mint_shrink-lo-80AutoARIMA/MinTrace_method-mint_shrink-hi-80AutoARIMA/MinTrace_method-mint_shrink-hi-90AutoARIMA/MinTrace_method-olsAutoARIMA/MinTrace_method-ols-lo-90AutoARIMA/MinTrace_method-ols-lo-80AutoARIMA/MinTrace_method-ols-hi-80AutoARIMA/MinTrace_method-ols-hi-90
0Australia2016-01-0126212.55355324705.94818025038.71507727386.39202927719.15892724646.51708423983.65684324130.064091…25267.79733824491.63061824663.06409125872.53058626043.96405826082.75348825010.87614125247.62380326917.88317427154.630835
1Australia2016-04-0125033.66712523337.26758823711.95469626355.37955426730.06666222942.95770322229.91683822387.407579…23836.80444423002.62021423186.86812824486.74076024670.98867424822.10209423616.73439323882.96633225761.23785726027.469796
2Australia2016-07-0124507.02719822640.02879823052.39641325961.65798326374.02559922568.28648821805.89219921974.283728…23294.24090822410.71983322605.86487323982.61694224177.76198324269.57872422944.38004323237.07928725302.07816225594.777406
3Australia2016-10-0125598.92861323575.66524324022.54741027175.30981627622.19198323113.07572622308.67186022486.342127…24154.48448723221.70618523427.73076624881.23820825087.26279025340.54992323905.43407024222.41093626458.68891126775.665777
4Australia2017-01-0126982.57679624669.53523825180.42128528784.73230829295.61835423779.26492122874.19422723074.098975…25155.00137224125.26891524352.70795225957.29479326184.73383026690.20092725051.35269825413.32833527967.07351828329.049155

​
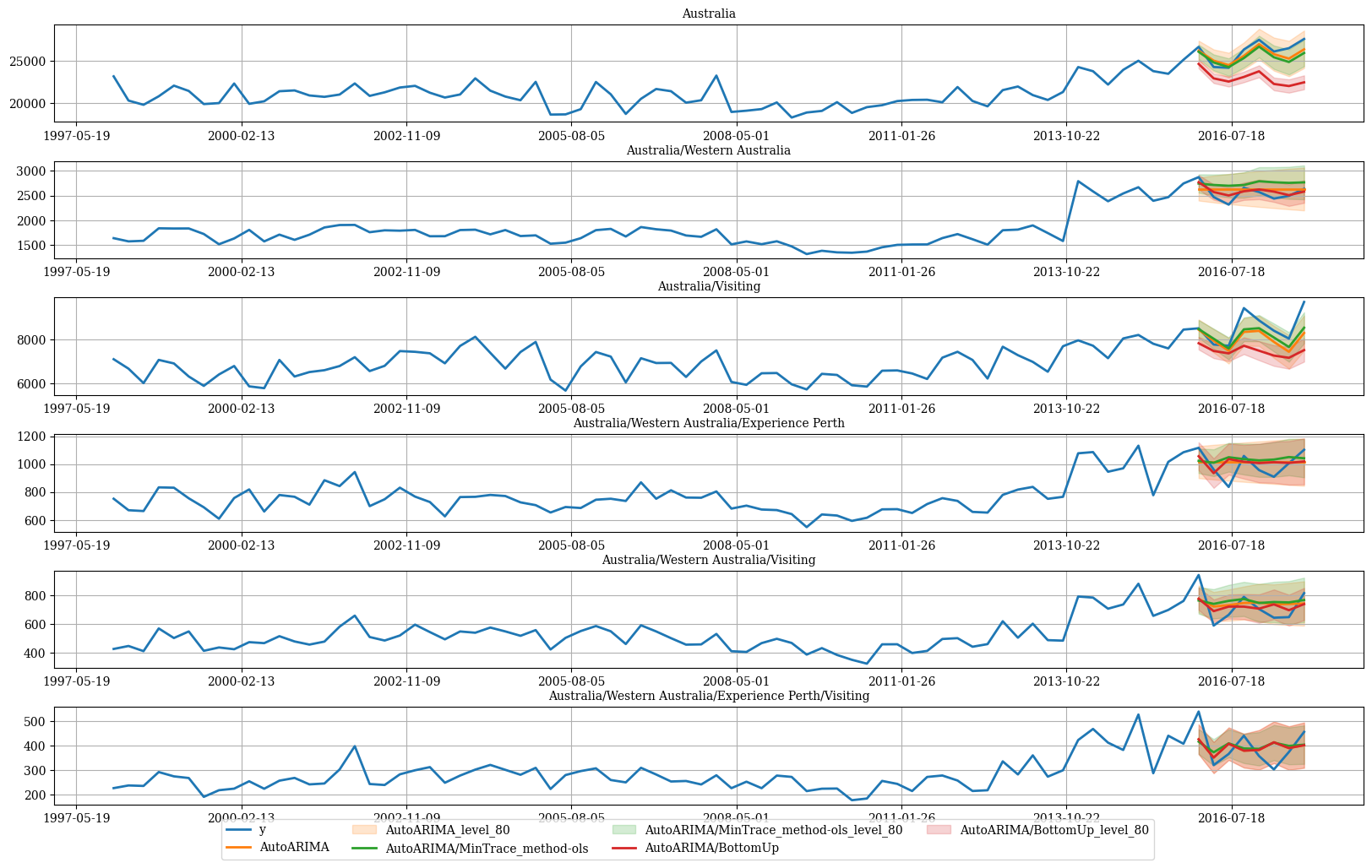
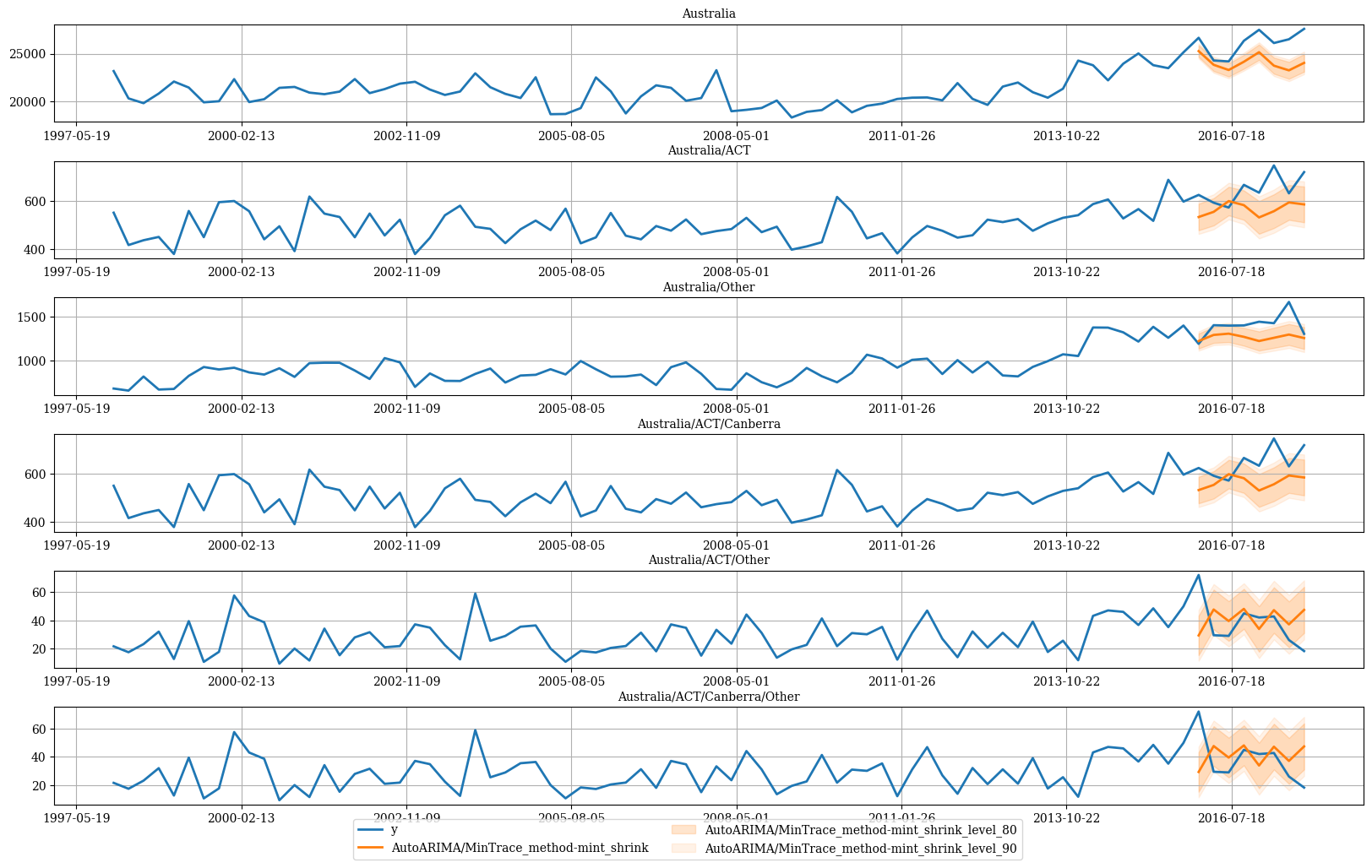
Plot forecasts

Then we can plot the probabilistic forecasts using the following function.

plot_df = Y_df.merge(Y_rec_df, on=['unique_id', 'ds'], how="outer")

​
Plot single time series

hplot.plot_series(
    series='Australia',
    Y_df=plot_df, 
    models=['y', 'AutoARIMA', 'AutoARIMA/MinTrace_method-ols'],
    level=[80]
)


# Since we are plotting a bottom time series
# the probabilistic and mean forecasts
# are the same
hplot.plot_series(
    series='Australia/Western Australia/Experience Perth/Visiting',
    Y_df=plot_df, 
    models=['y', 'AutoARIMA', 'AutoARIMA/BottomUp'],
    level=[80]
)

​
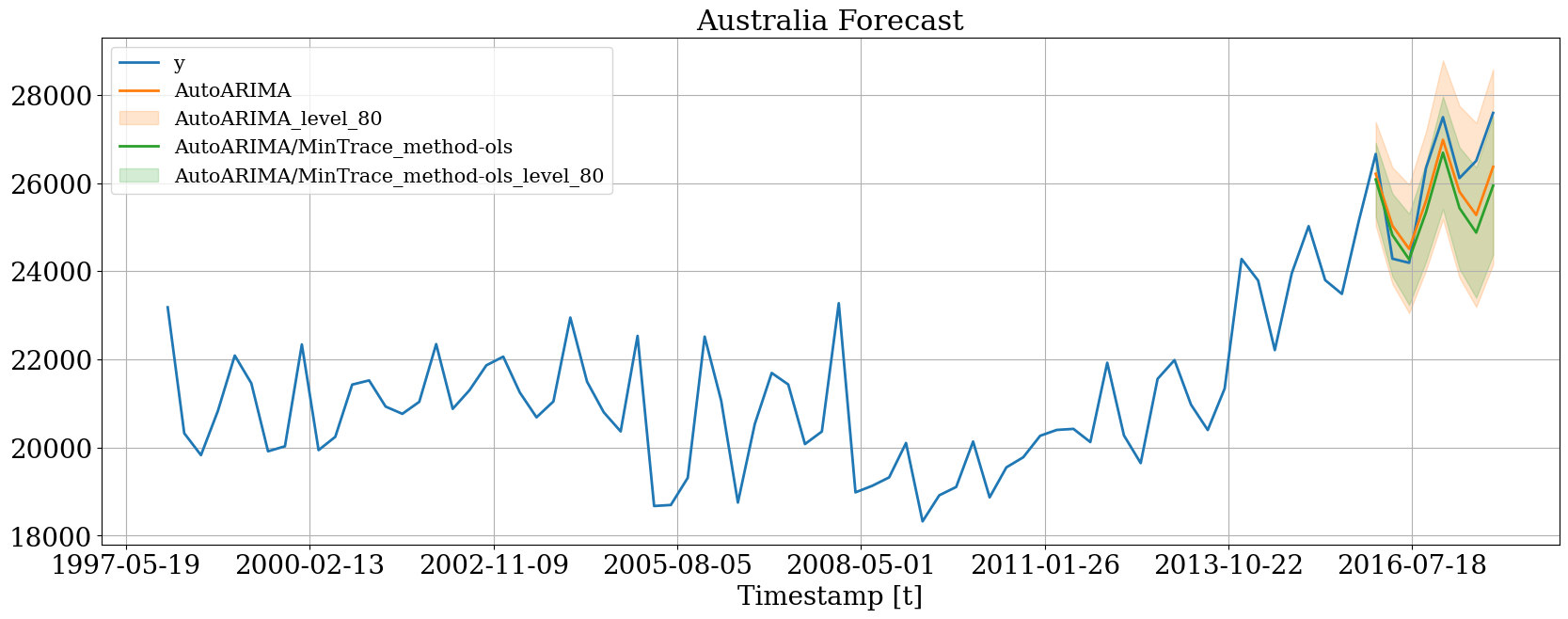
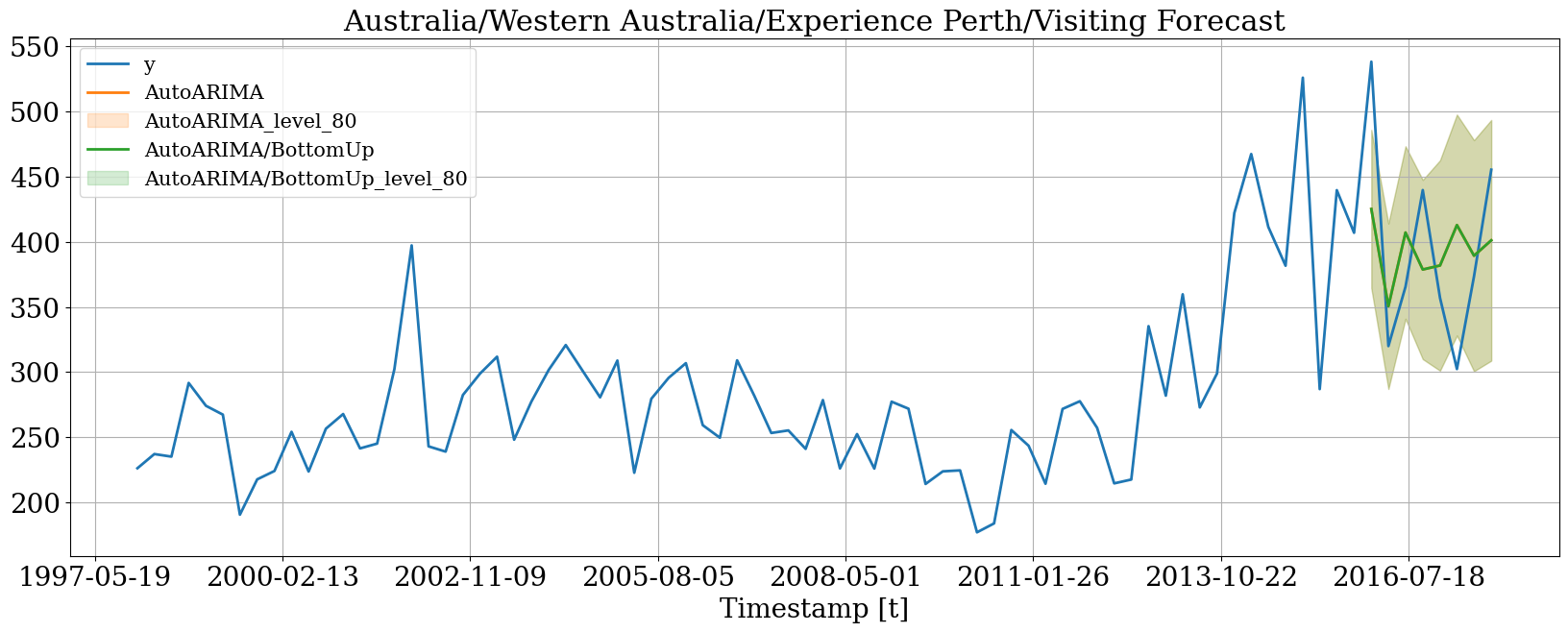
Plot hierarchichally linked time series

hplot.plot_hierarchically_linked_series(
    bottom_series='Australia/Western Australia/Experience Perth/Visiting',
    Y_df=plot_df, 
    models=['y', 'AutoARIMA', 'AutoARIMA/MinTrace_method-ols', 'AutoARIMA/BottomUp'],
    level=[80]
)


# ACT only has Canberra
hplot.plot_hierarchically_linked_series(
    bottom_series='Australia/ACT/Canberra/Other',
    Y_df=plot_df, 
    models=['y', 'AutoARIMA/MinTrace_method-mint_shrink'],
    level=[80, 90]
)

​
References

Non-Negative MinTraceBootstrap