1. Scale-dependent Errors
Mean Absolute Error
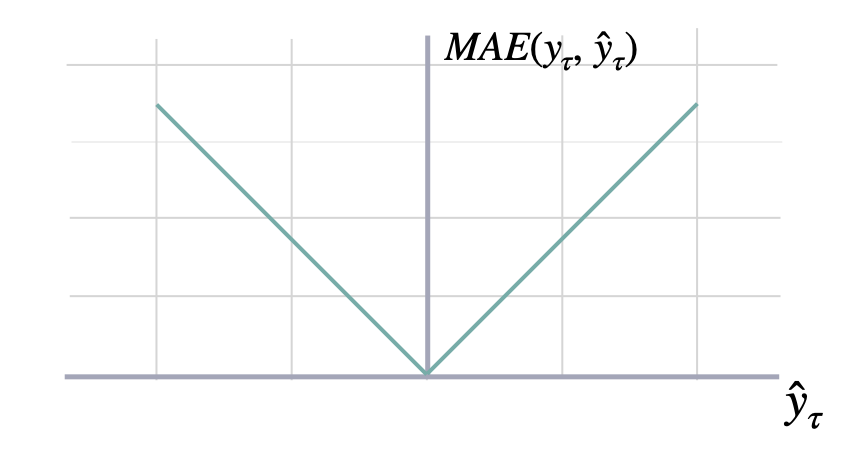
mae
Mean Squared Error
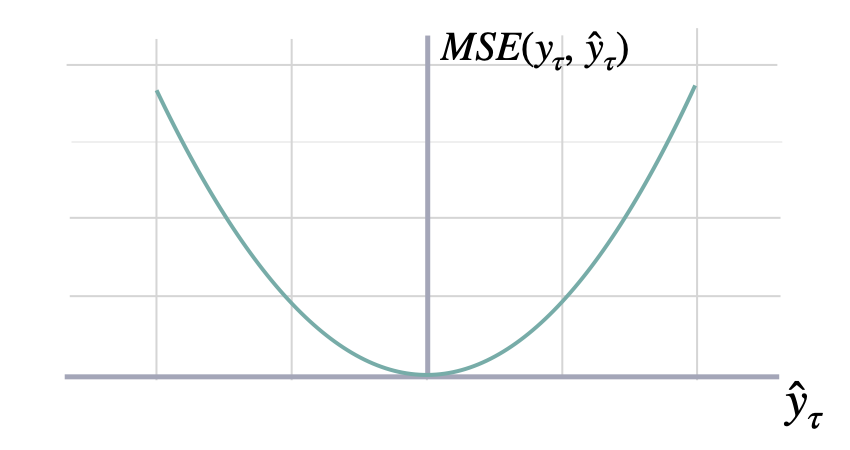
mse
Root Mean Squared Error
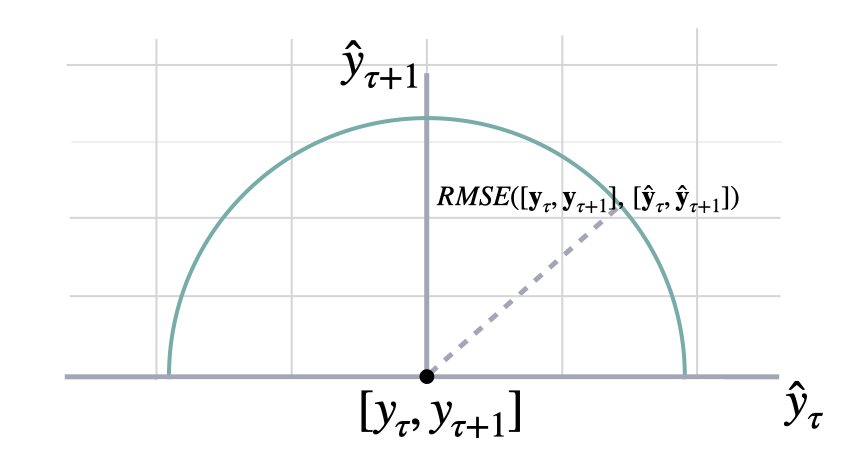
rmse
Bias
bias
Cumulative Forecast Error
cfe
Absolute Periods In Stock
pis
Linex
where must be .linex
- If a > 0, under-forecasting (y > y_hat) is penalized more.
- If a < 0, over-forecasting (y_hat > y) is penalized more.
- a must not be 0.
| Name | Type | Description | Default |
|---|---|---|---|
a | float | Asymmetry parameter. Must be non-zero. Defaults to 1.0. | 1.0 |
2. Percentage Errors
Mean Absolute Percentage Error
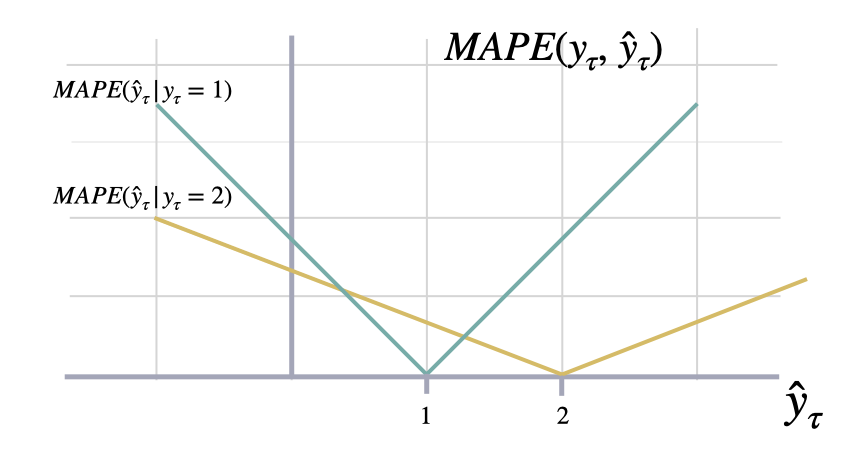
mape
Symmetric Mean Absolute Percentage Error
smape
3. Scale-independent Errors
Mean Absolute Scaled Error
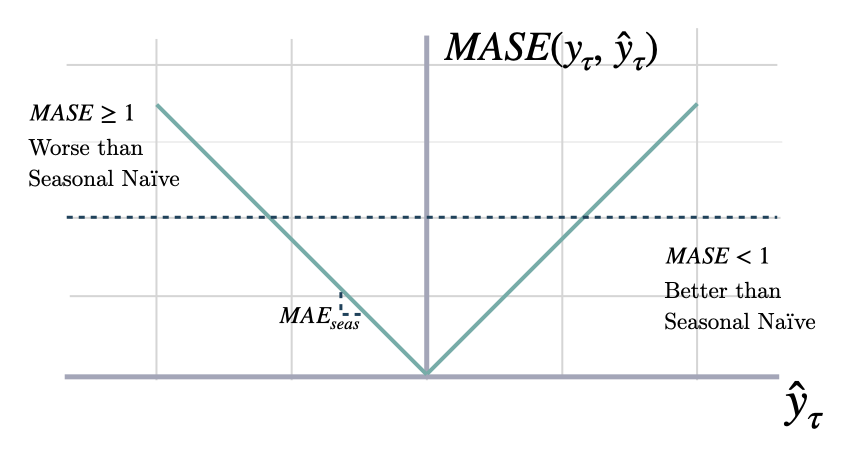
mase
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, actuals and predictions. | required |
models | list of str | Columns that identify the models predictions. | required |
seasonality | int | Main frequency of the time series; Hourly 24, Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1. | required |
train_df | pandas or polars DataFrame | Training dataframe with id and actual values. Must be sorted by time. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Relative Mean Absolute Error
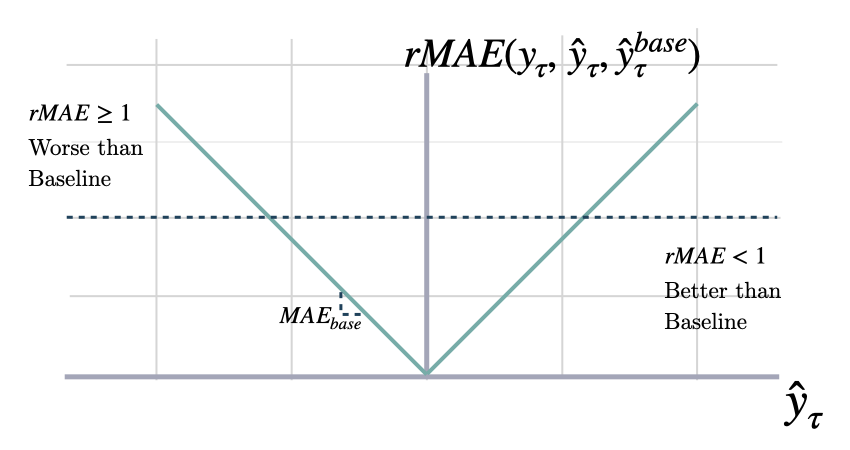
rmae
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | list of str | Columns that identify the models predictions. | required |
baseline | str | Column that identifies the baseline model predictions. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Normalized Deviation
nd
Mean Squared Scaled Error
msse
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, actuals and predictions. | required |
models | list of str | Columns that identify the models predictions. | required |
seasonality | int | Main frequency of the time series; Hourly 24, Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1. | required |
train_df | pandas or polars DataFrame | Training dataframe with id and actual values. Must be sorted by time. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Root Mean Squared Scaled Error
rmsse
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, actuals and predictions. | required |
models | list of str | Columns that identify the models predictions. | required |
seasonality | int | Main frequency of the time series; Hourly 24, Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1. | required |
train_df | pandas or polars DataFrame | Training dataframe with id and actual values. Must be sorted by time. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | required |
target_col | str | Column that contains the target. Defaults to ‘y’. | required |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | required |
| Type | Description |
|---|---|
| pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Scaled Absolute Periods In Stock
where .spis
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, actuals and predictions. | required |
models | list of str | Columns that identify the models predictions. | required |
train_df | pandas or polars DataFrame | Training dataframe with id and actual values. Must be sorted by time. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
4. Probabilistic Errors
Quantile Loss
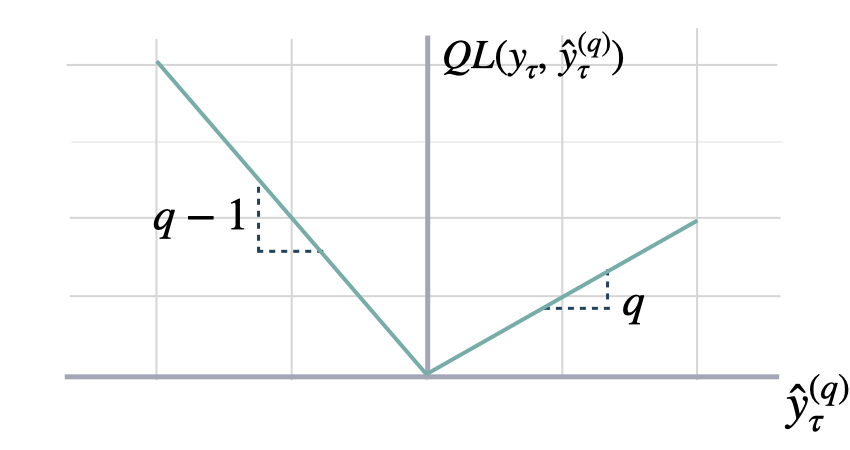
quantile_loss
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | dict from str to str | Mapping from model name to the model predictions for the specified quantile. | required |
q | float | Quantile for the predictions’ comparison. Defaults to 0.5. | 0.5 |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Scaled Quantile Loss
scaled_quantile_loss
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | dict from str to str | Mapping from model name to the model predictions for the specified quantile. | required |
seasonality | int | Main frequency of the time series; Hourly 24, Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1. | required |
train_df | pandas or polars DataFrame | Training dataframe with id and actual values. Must be sorted by time. | required |
q | float | Quantile for the predictions’ comparison. Defaults to 0.5. | 0.5 |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Multi-Quantile Loss
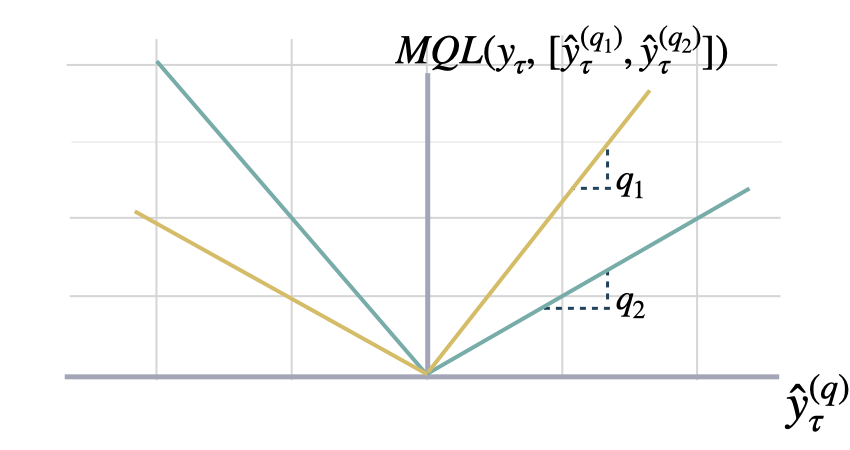
mqloss
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | dict from str to list of str | Mapping from model name to the model predictions for each quantile. | required |
quantiles | numpy array | Quantiles to compare against. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Scaled Multi-Quantile Loss
scaled_mqloss
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | dict from str to list of str | Mapping from model name to the model predictions for each quantile. | required |
quantiles | numpy array | Quantiles to compare against. | required |
seasonality | int | Main frequency of the time series; Hourly 24, Daily 7, Weekly 52, Monthly 12, Quarterly 4, Yearly 1. | required |
train_df | pandas or polars DataFrame | Training dataframe with id and actual values. Must be sorted by time. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Coverage
coverage
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | list of str | Columns that identify the models predictions. | required |
level | int | Confidence level used for intervals. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Calibration
calibration
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | dict from str to str | Mapping from model name to the model predictions. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
CRPS
Where is the an estimated multivariate distribution, and are its realizations.scaled_crps
y_hat compared to the observation y.
This metric averages percentual weighted absolute deviations as
defined by the quantile losses.
Parameters:
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, times, actuals and predictions. | required |
models | dict from str to list of str | Mapping from model name to the model predictions for each quantile. | required |
quantiles | numpy array | Quantiles to compare against. | required |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: dataframe with one row per id and one column per model. |
Tweedie Deviance
For a set of forecasts and observations , the mean Tweedie deviance with power is where the unit-scaled deviance for each pair is- are the true values, the predicted means.
- controls the variance relationship .
- When , this smoothly interpolates between Poisson () and Gamma () deviance.
tweedie_deviance
power parameter defines the specific compound distribution:
- 1: Poisson
- (1, 2): Compound Poisson-Gamma
- 2: Gamma
-
2: Inverse Gaussian
| Name | Type | Description | Default |
|---|---|---|---|
df | pandas or polars DataFrame | Input dataframe with id, actuals and predictions. | required |
models | list of str | Columns that identify the models predictions. | required |
power | float | Tweedie power parameter. Determines the compound distribution. Defaults to 1.5. | 1.5 |
id_col | str | Column that identifies each serie. Defaults to ‘unique_id’. | ‘unique_id’ |
target_col | str | Column that contains the target. Defaults to ‘y’. | ‘y’ |
cutoff_col | str | Column that identifies the cutoff point for each forecast cross-validation fold. Defaults to ‘cutoff’. | ‘cutoff’ |
| Type | Description |
|---|---|
IntoDataFrameT | pandas or polars DataFrame: DataFrame with one row per id and one column per model, containing the mean Tweedie deviance. |

